Chapter: Physics : Super Conducting Materials
Super Conductors
SUPER
CONDUCTORS
1 Introduction to Superconductivity
2 Properties of Superconductors
2.1 Critical magnetic field (Magnetic Property)
2.2 Diamagnetic property (Meissener effect)
2.3 SQUID (Superconducting Quantum Interference
Device)
2.4 Effect of heavy Current
2.5 Persistence of Current
2.6 Effect of pressure
2.7 Isotope effect
2.8 General properties
3 Types of Super Conductors
3.1 Difference between Type I and II
superconductors
3.2 Difference between High TC
4 High Temperature (High-Tc) Superconductors
5 Bcs Theory of Superconductivity
6 Applications of Superconductors
7 Engineering Applications
7.1 Cryotron
7.2 MAGLEV (MAGnetic LEVitation)
7.3 Josephson Devices
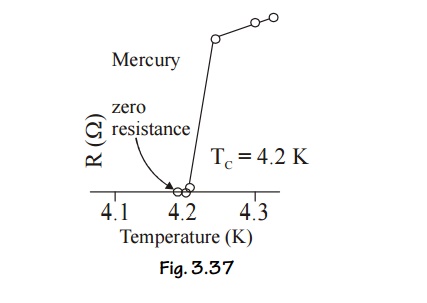
1 INTRODUCTION
TO SUPERCONDUCTIVITY
It was
thought that the electrical resistance of a conductor becomes zero only at
absolute zero temperature. But in 1911, H. Kammerlingh Onnes studied the
properties of mercury at very low temperature using liquid helium and is found
that the resistivity of mercury drops to zero at 4.2 K and changes into a
superconducting material
Mathiessen’s rule:
It states
that “the electrical resistivity

Definition
The
ability of certain metals and alloys exhibit almost zero electrical resistivity
when they are cooled to low temperature is known as superconducting. (ie.,
maximum conductivity with zero resistance at zero Kelvin)
Each of
these parameters is very dependent on the other two properties present.
Critical temperature ( TC ) (or)
Transition Temperature
The
temperature at which a normal conductor loses its resistivity and becomes a
superconductor is known as critical temperature (or) Transition temperature.
Every superconductor has its own critical temperature at which it passes over
into superconducting state. Depending on the transition temperature,
superconductors are classified into two groups are
Low temperature superconductors (LTS):The
superconductors which have low transition temperature (below
30K) are known as low temperature superconductors.
Example: Tin (3.2
K), Mercury (4.15 K).
High temperature superconductors (HTS): The superconductors
which
have high transition temperature (above 30K) is known as high
temperature superconductors.
Example: Barium -
Lanthanum - Copper - Oxide (BLCO) - 35 K
Yttrium -
Barium - Copper - Oxide - (Y Ba2 Cu3 O4) - 92
K
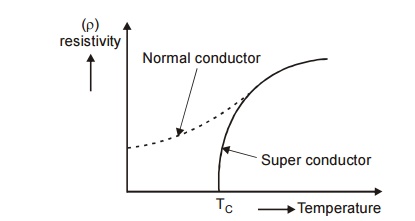
Fig.
3.26 Variation of electrical resistivity with temperature
2 PROPERTIES OF SUPERCONDUCTORS
At
Critical temperature, the following properties are observed.
The electrical resistivity drops to zero.
The magnetic flux lines are excluded (ejected out)
from the superconductors.
There is discontinuous change in the specific heat.
There are small changes in the thermal conductivity
and volume of the materials.
2.1 Critical
magnetic field (Magnetic Property)
A very
strong magnetic field applied to superconducting material it disappears super
conducting property this is called as critical magnetic field.

Fig.3.27
Critical magnetic field
It is
noted that when the temperature of a material increases, the value of critical
magnetic field decreases. Therefore the value of critical magnetic fields are
different for different materials.
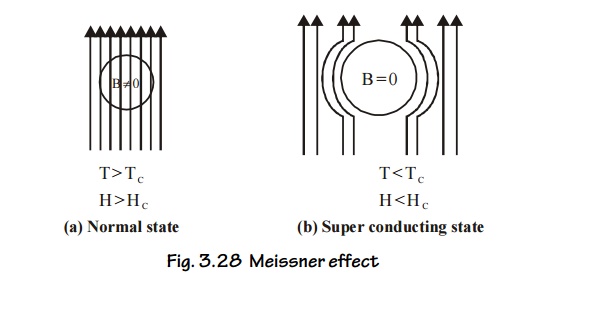
2.2
Diamagnetic property (Meissener effect)
If a
normal conducting material is placed in a magnetic field of flux density B, the
magnetic lines penetrate through the material.
Now the
material is cooled below its transition temperature when T TC then
the magnetic lines of forces are eapelled out from the material as shown in
figure.
We know
that, a diamagnetic material have the tendency to expel the magnetic lines of
force. Since the superconductor also expels tha magnetic lines of force and it
behaves as a perfect diamagnet. This behaviour was first observed by meissener
and hence called as meissener effect.
Meissener effect.
When the
superconducting material is subjected to a uniform magnetic field, under the
condition T TC and H HC, the magnetic flux lines are
excluded from the material. Thus the material exhibits perefect diamagnetism.
This phenomenon is called as meissner effect.
2.3 SQUID
(Superconducting Quantum Interference Device)
(We know that a small charge in
magnetic field produces variation in the flux quantum.)
It
consists of a superconducting ring which can have the magnetic field of quantum
values (1,2,3,....) of flux placed in between two Josephson junctions as shown
in figure.
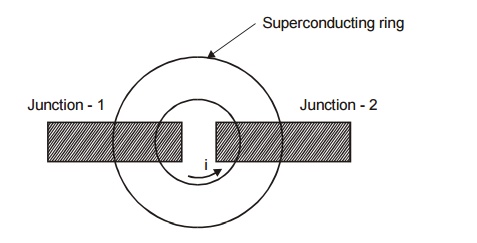
Fig.
3.29 SQUID
When the
magnetic field is applied perpendicular to the plane of the ring, the current
is induced at the two Josephon junctions.
The
induced current current produces the intereference pattern and if flows around
the ring so that the magnetic flux in the ring can have the quantum value of
magnetic field applied.
Applications
SQUID can be used to defect the variation of very
minute magnetic signals in terms of quantum flux.
It is used as a storage device for magnetic flux.
It is used to study earth qurkes and to remove
paramagnetic impurities.
Application of Meissner effect
It is a standard test to prove whether the material
is a perfect superconductor or not.
This effect is used for magnetic levitated train.
2.4 Effect
of heavy Current
The
superconducting property disappears when a heavy current flows, since current
flow will set up a magnetic field.
According
to Silsbee’s rule, for a superconducting wire, the induced current to destroy
the superconducting property is given by,

2.5
Persistence of Current
Persistence
current is one of the most important properties of a superconductor. When a
current of large magnitude is induced in a superconducting ring, the current
persisted in the ring even after the removal of the field at the temperature
below the critical temperature below the critical temperature, such a current
flows without reducing its strength is known is persistent current.

Fig.
3.30 Persistent Current
The
superconducting coil with persistent current acts as a magnet. It does not
require power supply to maintain its magnetic field.
2.6 Effect
of pressure
If
pressure increases, the critical temperature also increases. Therefore certain
materials are brought into the superconducting state by increasing the
pressure. Research is going on to get the superconducting state at room
temperature by applying heavy pressure.
2. 7
Isotope effect
The
presence of isotopes in superconductor change the transition temperature of the
superconductor. The transition temperature is found to be inversely
proportional to the square root of the atomic weight of the isotope (M).
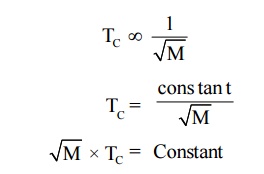
The
transition temperature of the heavier isotope is less than that of the lighter
isotope.
2.8
General properties
There is no change in elastic properties, photo
electric properties and crystal structure.
The transition temperature is unchanged with the
frequency variation.
3 TYPES OF
SUPER CONDUCTORS
Superconductors
are classified as follows
Based on the value of HC we have,
Type I (or) Soft superconductors
Type II (or) Hard superconductors
Based on the value of TC we have,
High temperature superconductors
Low temperature superconductors
Type I Superconductor
In type I
superconductor, the magnetic field is completely excluded from the material
below the critical magnetic field and the material loses its superconducting
property abruptly at.
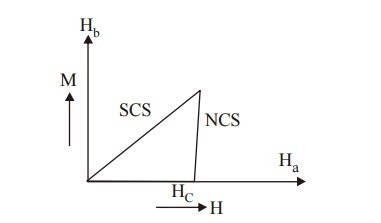
Fig.3.31
Type I Superconductor
Characteristics
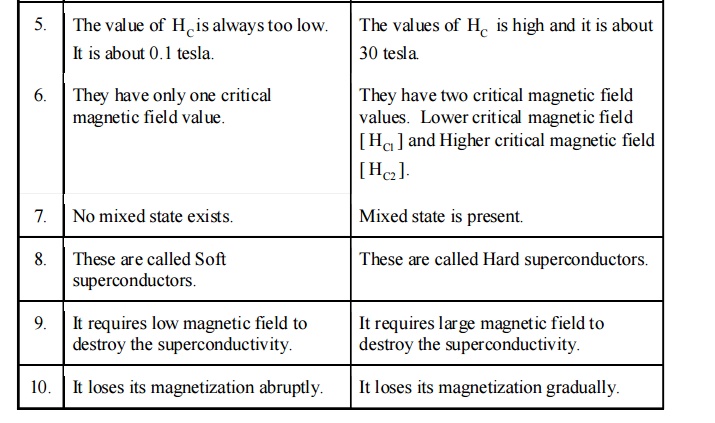
They exhibit complete Meissner Effect.
They have only one critical magnetic field value.
Below the material behaves as superconductor and
above the material behaves as normal conductor.
These are called as Soft superconductors.
Type II Superconductor
In type
II superconductor, the magnetic field is excluded from the material and the
material loses its superconducting property gradually rather than abruptly.
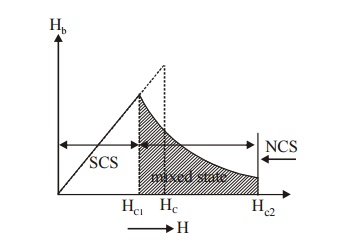
Fig. 3.32
Type II Superconductor
Characteristics
They do not exhibit a complete Meissner Effect.
They have two critical magnetic field values. Lower
critical magnetic filed [HCl] and Higher critical magnetic field [HC2].
Below HC1 the material behaves as
superconductor and above the material behaves as normal conductor. The region
in between [HCl] and [HC2] is called mixed state or
vortex region.
These are called as Hard superconductors.
Low TC Superconductors
The superconductors having the critical temperature
less than 20 K are known as low TC Superconductors or elemental
superconductors.
The Superconductors by BCS theory.
It is explained by BCS theory.
It is not so useful due to its low temperature
maintenance.
It is called as N-type superconductor.
High TC Superconductors
The superconductors having the critical temperature
greater than 100 K are known as high TC Superconductors or ceramic
or oxide superconductors.
The Superconductors is due to hole states.
It is explained by RVB theory proposed by Anderson.
It is very useful for commercial and engineering
purposes.
It is called as P-type superconductor.
3.1
Difference between Type I and II superconductors.

3.2 Difference
between High TC and Low TC superconductors
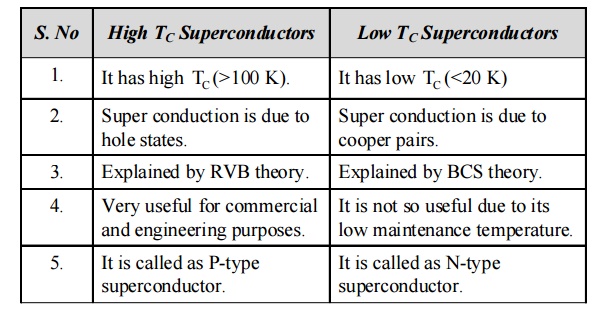
High TC Superconductors
1. It has
high TC (>100 K).
2. Super
conduction is due to hole states.
3.
Explained by RVB theory.
4. Very
useful for commercial and engineering purposes.
5. It is
called as P-type superconductor.
Low TC Superconductors
1. It has
low TC (<20 K)
2. Super
conduction is due to cooper pairs.
3.
Explained by BCS theory.
4. It is
not so useful due to its low maintenance temperature.
5. It is
called as N-type superconductor.
4 HIGH
TEMPERATURE (HIGH-TC) SUPERCONDUCTORS
Superconductors
with high values of critical temperature are called high temperature
superconductors (HTSC). The discovery of copper oxide based ceramic materials
by Bednorz and Muller in 1986 having critical temperature greater than 30 K
made a new era in the field of superconductivity.
The
superconductors have the critical temperature greater than 100 K are known as
high Superconductors or ceramic or oxide superconductors.
The
Superconductors is due to hole states and it is explained by RVB theory
proposed by Anderson. It is very useful for commercial and engineering
applications and it is called as P-type superconductors.
Characteristics
High TC Superconductors have high
temperatures.
They have a modified perovskite crystal structure.
Superconducting state is direction dependent.
These are oxides of copper with other elements.
These are reactive, brittle, and cannot be easily
modified or joined.
For high TC superconductors, liquid
Nitrogen is used instead of liquid helium.
5 BCS THEORY OF SUPERCONDUCTIVITY
The
properties of Type I superconductors were modeled successfully by the efforts
of John Bardeen, Leon Cooper, and Robert
Schrieffer in what is commonly called the BCS theory. A key conceptual
element in this theory is the pairing of electron close to the Fermi level into Cooper pairs through interaction with the crystal lattice. This
pairing results form a slight attraction between the electrons related to
lattice vibrations, the coupling to the lattice is called a phonon interaction.
Pairs of
electrons can behave very differently from single electrons which are fermions
and must obey the Pauli Exclusion Principle. The pairs of electrons act more
like bosons which can condense into the same energy level.
The
electron pairs have a slightly lower energy and leave an energy gap above them
on the order of 0.001 eV which inhibits the kind of collision interactions
which lead to ordinary resistivity. For temperatures such that the thermal
energy is less than the band gap, the material exhibits zero resistivity.
Bardeen, Cooper, and Schrieffer
received the Nobel Prize in 1972 for the development of the theory of
superconductivity.
Cooper Pairs
The
transition of a metal from the normal to the superconducting state has the
nature of a condensation of the electrons into a state which leaves a band gap
above them, this kind of condensation is seen with superfluid helium, but
helium is made up of bosons-multiple electrons can’t collect into a single
state because of the Pauli Exclusion Principle.
Froehlich
was first to suggest that the electrons act as pairs coupled by lattice
vibrations in the material. This coupling is viewed as an exchange of phonons,
phonons being the quanta of lattice vibration energy. Experimental
corroboration of an interaction with the lattice was provided by the isotopic
effect on the superconducting transition temperature.
The
boson-like of such electron pairs was further investigated by Cooper and they
are called “Cooper pairs”. The
condensation of Cooper pairs is the foundation of the BCS theory of
superconductivity.
A model of Cooper pair attraction
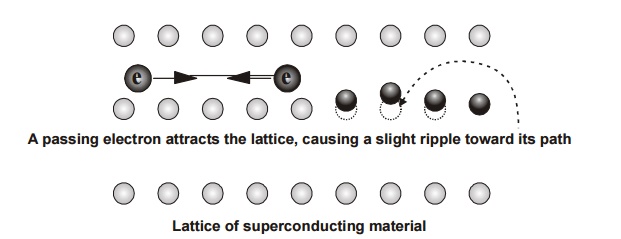
Fig.3.33
Cooper pair attraction
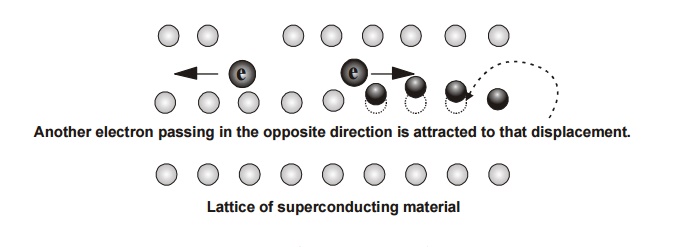
Fig .3.34
Cooper pair repulsion
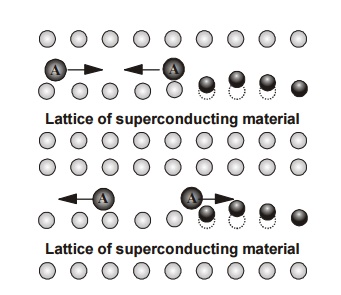
Fig. 3.35
Model of pair attraction
Ideas Leading to the BCS Theory
The BCS
theory of superconductivity has successfully described the measured properties
of Type I superconductors. It envisions resistance-free conduction of coupled
pairs of electrons called Cooper pairs. This theory is remarkable enough that
it is interesting to look at the chain of ideas which led to it.
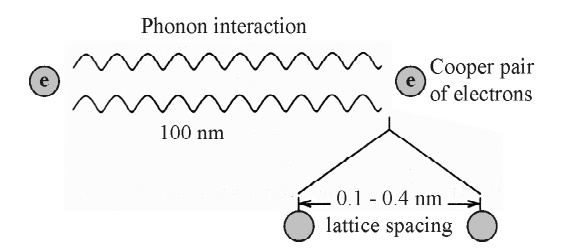
Fig.
3.36 Cooper pair (interaction)
One of the first steps toward a theory of
superconductivity was the realization that there must be a band gap separating
the charge carriers from the state of normal conduction.
A band gap was implied by the very fact that the
resistance is precisely zero. If charge carriers can move through a crystal
lattice without interacting at all, it must be because their energies are
quantized such that they do not have any available energy levels within reach
of the energies of interaction with the lattice.
A band gap is suggested by specific heats of
materials like vanadium. The fact that there is an exponentially increasing
specific hear as the temperature approaches the critical temperature from below
implies that thermal energy is being used to bridge some kind of gap in energy.
As the temperature increases, there is an exponential increase in the number of
particles which would have enough energy to cross the gap.
The critical temperature for superconductivity must
be a measure of the band gap, since the material could lose superconductivity
if thermal energy could get charge carriers across the gap.
The critical temperature was found to depend up on
isotopic mass. It certainly would not if the conduction was by free electrons
alone. The made it evident that the superconducting transition involved some
kind of interaction with the crystal lattice.
Single electrons could be eliminated as the charge
carriers in superconductivity since with a system of fermions you don’t get
energy gaps. All available levels up to the Fermi energy fill up.
The needed boson behavior was consistent with
having coupled pairs of electrons with opposite spins. The isotope effect
described above suggested that the coupling mechanism involved the crystal
lattice, so this gave rise to the phonon model of coupling envisioned with
Cooper pairs.
6 APPLICATIONS
OF SUPERCONDUCTORS
General Applications
Electric generators can be made by using
superconductors with smaller size, less weight and low energy consumption.
Superconductors can be used for the transmission of
power over very long distances.
Superconductors can be used in switching Devices.
The superconductors can be used in sensitive
electrical instruments.
It can be used as a memory or storage element in computers.
These are used to design Cryotron, Maglev,
Josephson Devices and SQUID.
DC superconducting motors are used in ship
propulsion and in large mills.
Superconducting magnetic field may be used to
launch satellite into orbit directly from the earth without use of rockets.
Ore separation can be done by using machines made
of superconducting magnets.
10.These are used in NMR (Nuclear Magnetic
Resonance) imaging equipments which is used for scanning purposes.
11.Superconductors are used for the detection of
brain tumor, defective cells, etc.,
12.Superconducting solenoids are used in magneto
hydrodynamic power generation to maintain the plasma in the body.
7 ENGINEERING
APPLICATIONS
7.1
Cryotron
It is a magnetically operated
current switch. The superconducting property disappear when the magnetic field
is greater than critical field ().
It
consists of a superconducting material [A] and it is surrounded by a super
conducting coil of wire [B].
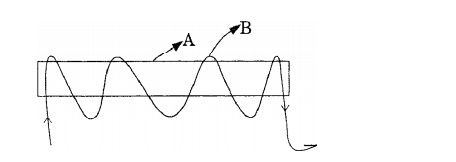
Fig.
3.38 Cryotron
When the
critical magnetic field of wire B exceeds or less than that of a
Superconducting material A, the current in A can be controlled by the current
in the material B, it can act as relay or switching elements and it can be used
as memory or storage element in computers.
7.2 MAGLEV
(MAGnetic LEVitation)
Maglev is
a magnetic levitated train, its works under the principal of Electromagnetic
induction. This train cannot move over the rail. Instead it floats above the
rails, so that it moves faster with speed of 500 Km/hr without any frictional
loss. It has two superconducting magnet on each side of the train and there is
guiding system consisting of ‘S” shaped coils on each side. Due to actions of
these magnets the train moves faster by levitation principle.
Working
This
train consists of superconducting magnets placed on each side of the train. The
train can run in a guiding system, which consists of serial ‘S’ shaped coil as
shown in figure.

Fig.
3.39 MGLEV
Initially
when the train starts, they slide on the rails. Now, when the train moves
faster, the superconducting magnets on each side of the train will induce a
current in the ‘S’ shaped coils kept in the guiding system.
This
induced current generates a magnetic force in the coils in such a way that the
lower half of ‘S’ shaped coil has the same magnetic pole as that of the
superconducting magnet in the train, while the upper half has the opposite
magnetic pole. Therefore, the total upward magnetic force acts on the train and
the train is levitated or raised above the rails and floats in the air.
Now, by
alternatively changing the poles of the superconducting magnet in the train,
alternating currents can be induced in ‘S’ shaped coils.
Thus,
alternating series of north and south magnetic poles are produced in the coils,
which pulls and pushes the superconducting magnets in the train and hence the
train is further moved. This can travel a speed of 500 km per hour.
7.3
Josephson Devices
Presistence
of current in an insulator which is separated by an insulator, even in the
absence of an applied voltage pairs of electrons moving through the potential
barrier induce the superconducting current. This effect is known as Josephson
effect.

Fig.
3.40 Josephson effect
A thin
layer of insulating material (10-50A°) is placed in between two superconducting
materials as shown in figure. When the voltage is applied across the
superconductors, current start flowing between the superconductors.
The flowing
current has both a.c and d.c components. The a.c current exists only up to
which the external voltage is applied whereas the d.c current exist even after
the removal of applied voltage. This effect is called Josephson effect.
Related Topics