Summary

Summary

·           Conditions for the binomial probability distribution are

(i) the trials are independent

(ii) the number of trials is finite

(iii) each trial has only two possible outcomes called success and failure.

(iv) the probability of success in each trial is a constant.

·           The probability for exactly x success in n independent trials is given by

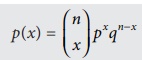 where x = 0,1,2,3…..n and q = 1 – p

·           The parameters of the binomial distributions are n and p

·           The mean of the binomial distribution is np and variance are npq

·           Poisson distribution as limiting form of binomial distribution when n is large, p  is small and np is finite.

·           The Poisson probability distribution is p(x) =  X = 0,1,2,3… Where λ = np

·           The mean and variance of the poisson distribtution is λ.

·           The λ is the only parameter of poisson distribution.

·           Poisson distribution can never be symmetrical.

·           It is a distribution for rare events.

·           Normal distribution is the limiting form of binomial distribution when n is large and neither p nor q is small

·           The normal probability distribution is given by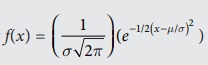 

·           The mean of the distribution is μ

·           The sd of the distribution is σ.

·           It is a symmetrical distribution

·           The graph of the distribution is bell shaped

·           In normal distribution the mean, median and mode are equal

·           The points of inflexion are μ – σ and μ + σ

·           The normal curve approaches the horizontal axis asymptotically

·           Area Property : In a normal distribution about 68% of the item will lie between μ – σ and μ + σ. About 95% will lie between are μ –2 σ and μ + 2σ . About 99% will lie between μ –3 σ and μ +3 σ.

·           Standard normal random variate is denoted as Z = (X – μ)/σ

·           The standard normal probability distribution is 

·           The mean of the distribution is zero and SD is unity

·           The points of inflexion are at z = –1 and z = +1