Definition, Properties, Derivation, Formulas, Solved Example Problems - Poisson Distribution | 12th Business Maths and Statistics : Chapter 7 : Probability Distributions
Chapter: 12th Business Maths and Statistics : Chapter 7 : Probability Distributions
Poisson Distribution
Distribution
The following are the two types of Theoretical distributions :
1. Discrete distribution 2. Continous distribution
Discrete distribution
The binomial and Poisson distributions are the most useful theoretical distributions for discrete variables.
POISSON
DISTRIBUTION
Poisson distribution was
derived in 1837 by a French Mathematician Simeon D. Poisson. If n is large,,
the evaluation of the binomial probabilities can involve complex computations,
in such a case, a simple approximation to the binomial probabilities could be
use. Such approximation of binomial when n is large and p is close to zero is
called the Poisson distribution.
Poisson distribution
occurs when there are events which do not occur as a definite number on trials
but an events occurs rarely and the following examples may be analysed:
(i) Number of bacteria
in one cubic centimeter.
(ii) Number of printing
mistakes per page in a text book
(iii) the number of
alpha particles emitted by a radioactive substance in a fraction of a second.
(iv) Number of road
accidents occurring at a particular interval of time per day.
(v) Number of lightnings
per second.
Poisson distribution is
a limiting case of binomial distribution under the following conditions :
i.
n, the number of trials is
indefinitely large i.e n → ∞ .
ii.
p, the constant probability
of success in each trial is very small, i.e. p → 0
iii.
np = λ is finite. Thus p = λ/n = l and q=1-( λ/n) where λ is a
positive real number.
Definition 7.2
A random variable X is
said to follow a Poission distribution with parameter λ if it assumes only
non-negative values and its probability mass function is given by
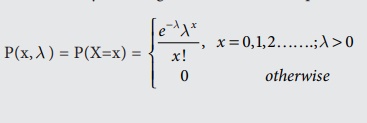
Derivation of Mean and variance of Poisson distribution
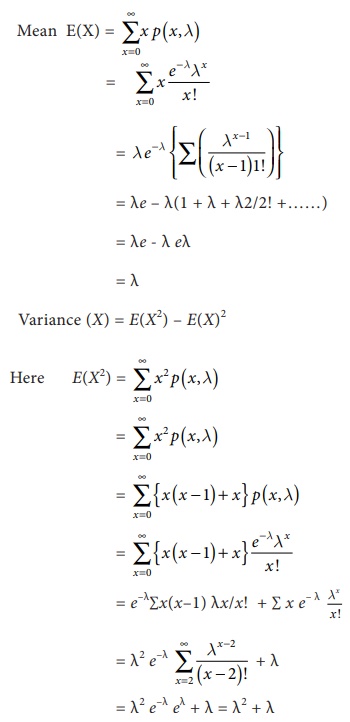
Variance (X) = E(X2)
– E(X)2
= λ2 + λ –
(λ)2
= λ
Properties of Poisson distribution :
1. Poisson distribution
is the only distribution in which the mean and variance are equal .
Example
7.14
In a Poisson
distribution the first probability term is 0.2725. Find the next Probability term
Solution :
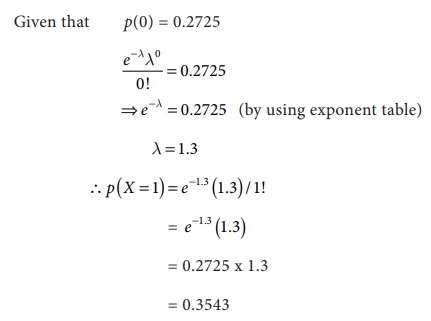
Example
7.15
In a book of 520 pages,
390 typo-graphical errors occur. Assuming Poisson law for the number of errors
per page, find the probability that a random sample of 5 pages will contain no
error.
Solution :
The average number of
typographical errors per page in the book is given by λ = (390/520) = 0.75.
Hence using Poisson
probability law, the probability of x errors per page is given by
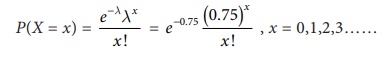
The required probability that a random sample of 5 pages will contain no error is given by : [P(X=0)]5 = (e-0.75)5 = e-3.75
Example
7.16
An insurance company has
discovered that only about 0.1 per cent of the population is involved in a
certain type of accident each year. If its 10,000 policy holders were randomly
selected from the population, what is the probability that not more than 5 of
its clients are involved in such an accident next year? ( e−10 = .000045)
Solution :
p = probability that a
person will involve in an accident in a year
= 0.1/100 = 1/1000
given n = 10,000
so, λ = np = 10000 (1/1000) = 10
Probability that not
more than 5 will involve in such an accident in a year
P(X < 5)= P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)
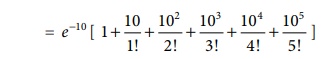
= 0.06651
Example
7.17
One fifth percent of the
the blades produced by a blade manufacturing factory turn out to be defective.
The blades are supplied in packets of 10. Use Poisson distribution to calculate
the approximate number of packets containing no defective, one defective and
two defective blades respectively in a consignment of 1,00,000 packets (e–0.2
=.9802)
Solution :
P = 1/5/100 = 1/500
=0.002
n = 10 .
λ = np = 0.02
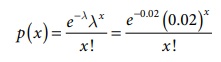
(i) Number of packets
containing no defective = N p(o) = 1,00,000 × e–0.02
= 98020
(ii) Number of packets
containing one defective = N p(1) = 1,00,000 × 0.9802 × 0.02
= 1960
(iii) Number of packets containing 2 defectives = N p(2) = 20
Example
7.18
If the probability that
an individual suffers a bad reaction from injection of a given serum is 0.001,
determines the probability that out of 2,000 individuals (a) exactly 3, and (b)
more than 2 individuals will suffer a bad reaction.
Solution :
Consider a 2,000
individuals getting injection of a given serum , n = 2000
Let X be the number of
individuals suffering a bad reaction.
Let p be the probability
that an individual suffers a bad reaction = 0.001
and q = 1– p = 1– 0.001 = 0.999
Since n is large and p
is small, Binomial Distribtuion approximated to poisson distribution
So, λ = np = 2000 ×
0.001 = 2
(i) Probability out of
2000, exactly 3 will suffer a bad reaction is

(ii) Probability out of
2000, more than 2 individuals will suffer a bad reaction
= P(X > 2)
= 1– [( P X( ≤ 2)]
= 1 – [P(x = 0) + P(x = 1) + P(x = 2)]
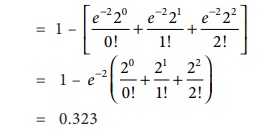
= 0.323
Example
7.19
When counting red blood
cells, a square grid is used, over which a drop of blood is evenly distributed.
Under the microscope an average of 8 erythrocytes are observed per single
square. What is the probability that exactly 5 erythrocytes are found in one
square?
Solution :
Let X be a random
variable follows poisson distribution with number of erythrocytes.
Hence, Mean λ = 8
erythrocytes/single square
P(exactly 5 erythrocytes
are in one square) = P(X = 5) =
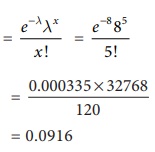
The probability that exactly 5 erythrocytes are found in one square is 0.0916. i.e there are 9.16% chances that exactly 5 erythrocytes are found in one square.
Example
7.20
Assuming one in 80
births is a case of twins, calculate the probability of 2 or more sets of twins
on a day when 30 births occur.
Solution :
Let x devotes the set of
twins on a day
P(twin birth) = p = 1/80
= 0.0125 and n = 30
The value of mean λ = np
= 30 × 0.0125 = 0.375
Hence, X follows poisson
distribution with p(x) = ![]()
The probability is
P(2 or more) = 1 – [p (x
= 0) + p (x = )] =
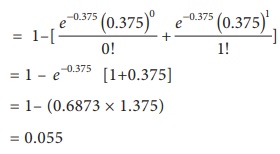
Related Topics