Definition, Properties, Derivation, Formulas, Solved Example Problems - Binomial distribution | 12th Business Maths and Statistics : Chapter 7 : Probability Distributions
Chapter: 12th Business Maths and Statistics : Chapter 7 : Probability Distributions
Binomial distribution
Distribution
The following are the two types of Theoretical distributions :
1. Discrete distribution 2. Continous distribution
Discrete distribution
The binomial and Poisson distributions are the most useful theoretical distributions for discrete variables.
Binomial
distribution
Binomial distribution
was discovered by James Bernoulli(1654_1705) in the year 1700 and was first
published posthumously in 1713 , eight years after his death.
A random experiment
whose outcomes are of two types namely success S and failure F, occurring with
probabilities p and q respectively, is called a Bernoulli trial.
Some examples of
Bernoulli trials are :
(i) Tossing of a coin
(Head or tail)
(ii) Throwing of a die
(getting even or odd number)
Consider a set of n
independent Bernoullian trails (n being finite) in which the probability
‘p’ of success in any trial is constant , then q = 1–p ,
is the probability of failure. The probability of x successes and
consequently (n–x) failures in n independent trials, in a specified
order (say) SSFSFFFS….FSF is given in the compound probability theorem by the
expression
P(SSFSFFFS…..FSF) =
P(S)P(S)P(F)P(S)x…….xP(F)P(S)P(F)
p.p.qp………………q.p.q
p.p. p.p.
……q.q.q.q.q.q
{x factors}
{(n–x) factors}
pxq(n−x)
x successes in n trials
can occur in nCx ways and the probability for each of
these ways is same namely px qn−x .
The probability
distribution of the number of successes, so obtained is called the binomial
probability distribution and the binomial expansion is (q + p)n
Definition 7.1
A random variable X
is said to follow binomial distribution with parameter n and p,
if it assumes only non- negative value and its probability mass function in
given by
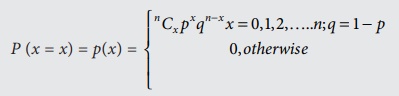
Note
Any random variable
which follows binomial distribution is known as binomial variate i.e X ~
B(n,p) is a binomial variate.
The Binomial
distribution can be used under the following conditions :
1. The number of trials
‘n’ finite
2. The trials are
independent of each other.
3. The probability of
success ‘p’ is constant for each trial.
4. In every trial there
are only two possible outcomes – success or failure.
Derivation of the Mean and Variance of Binomial distribution :

∴
Variance = E(X2) – E(X)2
= n2p2 – np2
+ np – n2p2
= np(1–p) = npq
Hence, mean of the BD is
np and the Variance is npq.
Properties of Binomial
distribution
1. Binomial distribution
is symmetrical if p = q = 0.5. It is skew symmetric if p ≠
q. It is positively skewed if p < 0.5 and it is negatively skewed
if p > 0.5
2. For Binomial
distribution, variance is less than mean
Variance npq = (np)q
< np
Example
7.1
A and B play a game
in which their chance of winning are in the ratio 3:2 Find A’s chance
of winning atleast three games out of five games played.
Soltion:
Let ‘p’ be the
probability that ‘A’ wins the game. Then we are given n = 5, p
= 3/5, q = 1 – 3/5 = 2/5 (since q =
1–p)
Hence by binomial
probability law, the probability that out of the 5 games played, A wins ‘x’
games is given by

The required probability
that ‘A’ wins atleast three games is given by
P ( X ≥ 3) = P(X = 3) + P(X = 4) + P(X = 5)
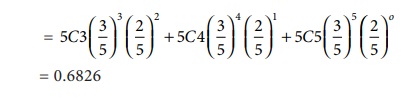
Example
7.2
A fair coin is tossed 6
times. Find the probability that exactly 2 heads occurs.
Solution :
Let X be a random variable
follows binomial distribution with probability value p = 1/2 and q = 1/2
Prob: that exactcy 2
heads occur are as follows
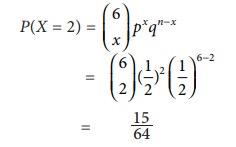
Example
7.3
Verify the following statement: The mean of a Binomial distribution is
12 and its standard deviation is 4.
Solution:
Mean: np = 12
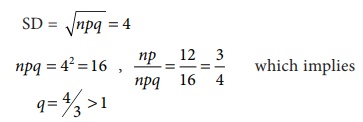
Since p + q cannot be
greater than unity, the Statement is wrong
Example
7.4
The probability that a
student get the degree is 0.4 Determine the probability that out of 5 students
(i) onewill be graduate (ii) atleast one will be graduate
Solution:
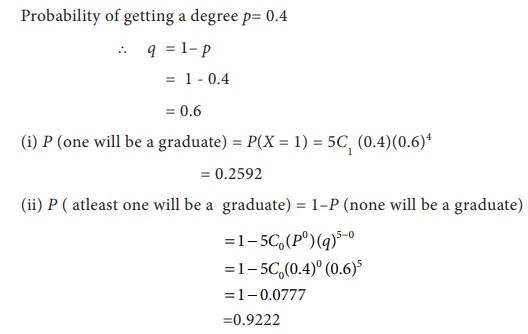
Example
7.5
In tossing of a five
fair coin, find the chance of getting exactly 3 heads.
Solution :
Let X be a random
variable follows binomial distribution with p = q = 1 /2
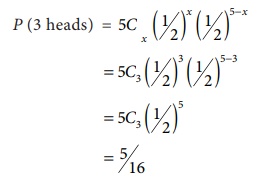
Example
7.6
The mean of Binomials
distribution is 20 and standard deviation is 4. Find the parameters of the
distribution.
Solution
The parameters of
Binomial distribution are n and p
For Binomial
distribution Mean = np =20
Standard deviation = √npq
= 4
∴ npq = 16
⇒ npq/np = 16/20 = 4/5
q = 4/5
⇒ p = 1–q = 1– (4/5) =
1/5
Since np = 20
n = 20/p
n= 100
Example
7.7
If x is a
binomially distributed random variable with E(x) =2 and van (x)
= 4/3 . Find P(x =
5)
Solution:
The p.m.f. Binomial
distribution is
p(x) = nCx
px qn−x
Given that E(x) =2
For the Binomial
distribution mean is given by np = 2 ... (1)
Given that var (x) = 4/3
For Binomial
distribution variance is given by npq= 4/3 ... (2)
(2)/(1) = 4/6 = 2/3
q = 2/3 and p = 1–2/3 = 1/3
Substitute is (1) we get
n = 6
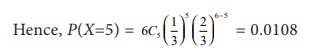
Example
7.8
If on the average rain
falls on 9 days in every thirty days, find the probability that rain will fall
on atleast two days of a given week.
Solution :
Probability of raining
on a particular day is given by p = 9/30 = 3/10 and
q = 1–p = 7/10.
The BD is P(X = x) = nCx
px qn−x
There are 7 days in a
week P(X = x) = 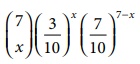
The probability of
raining for atleast 2 days is given by

Therefore the required probability =
1– [P(x = 0) +P(x = 1)]
= 1– {0.082+ 0.247]
= 0.6706
Example
7.9
What is the probability
of guessing correctly atleast six of the ten answers in a TRUE/ FALSE objective
test?
Solution :
Probability p of
guessing an answer correctly is p = 1/2
q = 1/2
Probability of guessing
correctly x answers in 10 questions
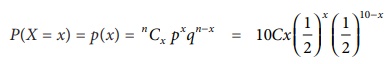
The required probability
P(X ≥ 6) = P(6) + P(7) + P(8) + P(9) + P(10)
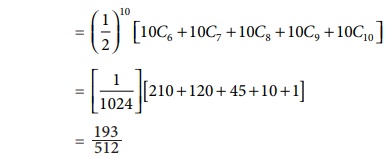
Example
7.10
If the chance of running
a bus service according to schedule is 0.8, calculate the probability on a day
schedule with 10 services : (i) exactly one is late (ii) atleast one is late
Solution :
Probability of bus
running late is denoted as p = 1-0.8 = 0.2
Probability of bus
running according to the schedule is q
= 0.8
Also given that n = 10
The binomial
distribution is p(x) = 10Cx (0.2)x (0.8)10-xt.
(i) probability that
exactly one is late P(y=1) = 10C1pq9
= 10C1 (0.2) (0.8)9
(ii) probability that at
least one is late
= 1 – probability that none is late
= 1 – p(x=0)
= 1– (0.8)10
Example
7.11
The sum and product of
the mean and variance of a binomial distribution are 24 and 128. Find the
distribution.
Solution :
For Binomial
Distribution the mean is np and
varaiance is npq
Given values are np +
npq = 24
np(1 + q) = 24 – (1)
Other term np × npq =
128
n2p2q=128 - (2)
From (1) we get np =
24/(1+q) which implies n2p2 = (24/(1+q))2
Substitute this value in
equation (2) we get
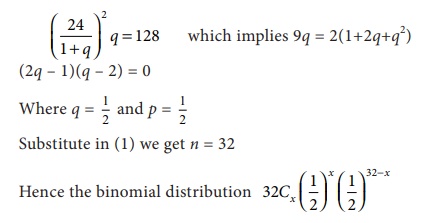
Example
7.12
Suppose A and B
are two equally strong table tennis players. Which of the following two events
is more probable:
(a) A beats B exactly in
3 games out of 4 or
(b) A beats B exactly in
5 games out of 8 ?
Solution :
Here p = q = 1/2
(a) probability of A
beating B in exactly 3 games out of 4

= 1/4 = 25%
(b) probability of A
beating B in exactly 5 games out of 8
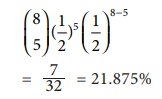
= 7/32 = 21.875%
Clearly, the first event is more probable.
Example
7.13
A pair of dice is thrown
4 times. If getting a doublet is considered a success, find the probability of
2 successes.
Solution :
In a throw of a pair of
dice the doublets are (1,1) (2,2) (3,3) (4,4) (5,5) (6,6)
Probability of getting a
doublet p = 6/36 = 1/6
⇒
q = 1 – p = 5/6 and also n = 4 is given
The probabitliy of
successes 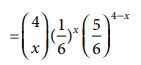
Therefore the
probability of 2 successes are
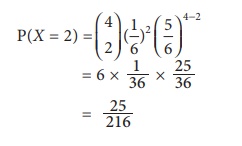
Related Topics