Sum to n/infinite terms of a G.P.(Geometric Progression)

Sum to n terms of a G.P.

A series whose terms are in Geometric progression is called Geometric series.

Let a, ar, ar² , ...ar^n-1 , ... be the Geometric Progression.

The sum of first n terms of the Geometric progression is

S_n  = a +ar + ar ² +  + ar^{n −2} +ar^n−1                                                       ... (1)

Multiplying both sides by r, we get rS_n  = ar +ar² + ar³ +  + ar^{n −1} +arⁿ           … (2)

(2)−(1) gives rS_n − S _n  = arⁿ –a

S_n (r −1) = a(rⁿ –1)

Thus, the sum to n terms is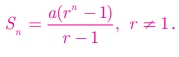 

Note

The above formula for sum of first n terms of a G.P. is not applicable when r = 1.

If r = 1 , then

S_n  = a + a + a + + a = na

Progress Check

1. A series whose terms are in Geometric progression is called _______.

2. Whenr = 1 , the formula for finding sum to n terms of a G.P. is ______.

3. Whenr ≠ 1 , the formula for finding sum to n terms of a G.P. is ______.

Sum to infinite terms of a G.P.

The sum of infinite terms of a G.P. is given by a + ar +ar ²  + ar ³ +….. =  a /(1-r), -1 < r < 1

Example 2.46 Find the sum of 8 terms of the G.P. 1, − 3, 9, −27…

Solutions

Here the first term a = 1 , common ratio r = -3/1 = -3 < 1, Here n = 8.

Sum to n terms of a G.P. is 

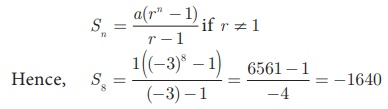
Example 2.47

Find the first term of a G.P. in which S₆ = 4095 and r = 4.

Solution

Common ratio = 4 > 1 , Sum of first 6 terms S₆  = 4095 

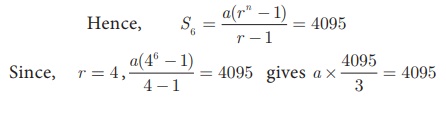
First term a = 3 .

Example 2.48

How many terms of the series 1 + 4 + 16 +   make the sum 1365 ?

Solution

Let n be the number of terms to be added to get the sum 1365

4ⁿ  = 4096 then 4ⁿ  = 4⁶

n = 6

Example 2.49 

Find the sum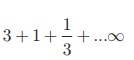 

Solution Here a = 3 ,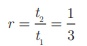 

Sum of infinite terms = 

Example 2.50 

Find the rational form of the number 0.6666¼

Solution

We can express the number 0.6666¼as follows

0.6666… = 0.6 + 0.06 + 0.006 + 0.0006 +

We now see that numbers 0.6, 0.06, 0.006 ... forms an G.P. whose first term a = 0.6

and common ration r = 0.06 / 0.6 = 0.1 . Also − 1 < r = 0.1 < 1

Using the infinite G.P. formula, we have

0.6666... = 0.6 + 0.06 + 0.006 + 0.0006 +  ...  =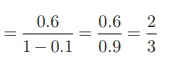 

Thus the rational number equivalent of 0.6666 is 2/3

Example 2.51

Find the sum to n terms of the series 5 + 55 + 555 + ...

Solution

The series is neither Arithmetic nor Geometric series. So it can be split into two series and then find the sum.

Example 2.52

Find the least positive integer n such that 1 + 6 + 6² + + 6ⁿ > 5000

Solution

We have to find the least number of terms for which the sum must be greater than 5000.

That is, to find the least value of n. such that     S_n > 5000

We have

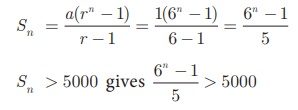
 6ⁿ -1  > 25000 gives 6ⁿ > 25001 

Since,       6⁵ = 7776 and 6⁶  =46656

The least positive value of n is 6 such that    1 + 6 + 6² +  + 6ⁿ > 5000.

Example 2.53

A person saved money every year, half as much as he could in the previous year. If he had totally saved ₹ 7875 in 6 years then how much did he save in the first year?

Solution

Total amount saved in 6 years is S₆ = 7875

Since he saved half as much money as every year he saved in the previous year,

We have r = ½ < 1

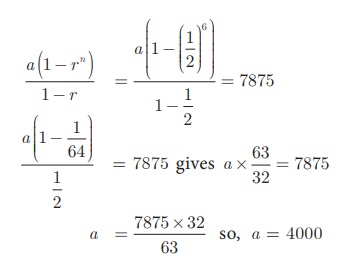
The amount saved in the first year is ₹ 4000.