Special Series

Special Series

There are some series whose sum can be expressed by explicit formulae. Such series are called special series.

Here we study some common special series like

(i) Sum of first ‘n’ natural numbers

(ii) Sum of first ‘n’ odd natural numbers.

(iii) Sum of squares of first ‘n’ natural numbers.

(iv) Sum of cubes of first ‘n’ natural numbers.

We can derive the formula for sum of any powers of first n natural numbers using the expression (x + 1)^{k +1} − x ^{k +1} . That is to find 1^k + 2^k + 3^k + ... + n^k we can use the expression (x + 1)^{k +1} − x ^{k +1} .

1. Sum of first n natural numbers

To find1 + 2 + 3 + + n , let us consider the identity (x + 1)² − x ² = 2x + 1

When x = 1 , 2² − 1² = 2(1) + 1

When x = 2 , 3² − 2²  = 2(2) + 1

When x = 3 , 4² − 3²  = 2(3) + 1

                       :     :         :

When x = n −1 , n ² − (n −1)² = 2(n −1) + 1

When x = n −1 , (n + 1)²  - n ²= 2(n) + 1

Adding all these equations and cancelling the terms on the Left Hand side, we get,

(n + 1)² −1² = 2(1 + 2 + 3 +  + n ) + n

n ² + 2n= 2(1 + 2 + 3 +  + n ) + n

2(1 + 2 + 3 +  + n) = n ²  + n = n (n + 1)

1 + 2 + 3 +  + n= [n (n + 1)] / 2

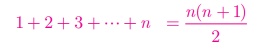
2. Sum of first n odd natural numbers

1 + 3 + 5 + + (2n −1)

It is an A.P. with a = 1 , d = 2 and l = 2n −1

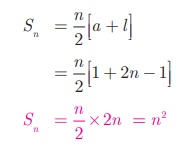
3. Sum of squares of first n natural numbers

To find1² + 2² + 3² + + n² , let us consider the identity (x + 1)³ − x ³  = 3x ²  + 3x + 1

When x = 1 , 2 ³ − 1³  = 3(1)²  + 3(1) + 1

When x = 2 , 3 ³ − 2 ³  = 3(2)²  + 3(2) + 1

When x = 3 , 4 ³ − 3 ³  = 3(3)² + 3(3) + 1

               :            :                     :

When x = n −1 , n ³ − (n −1)³ = 3(n −1)² + 3(n −1) + 1

When x = n , (n + 1)³ −n³ = 3n ² + 3n + 1

Adding all these equations and cancelling the terms on the Left Hand side, we get,

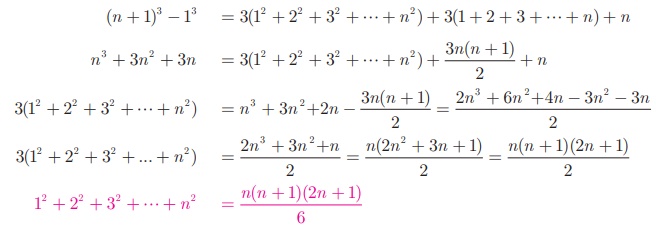
4. Sum of cubes of first n natural numbers

To find 1³ + 2³ + 3³ + + n³ , let us consider the identity 

(x + 1)⁴ − x ⁴  = 4x ³ + 6x ² + 4x + 1

When x = 1 , 2 ⁴ − 1⁴ = 4(1)² + 4(1) + 1

When x =2 , 3⁴ − 2 ⁴ = 4(2)³ + 4(2) + 1

When x = 3 , 4⁴ − 3 ⁴ = 4(3)³ + 6(3) + 1

               :                    :               :

When x = n −1 ,n⁴ − (n −1)⁴ = 4(n −1)³  + 4(n −1) + 1

When x = n , (n + 1)⁴ −n⁴  = 4n³ + 6n² + 4n + 1

Adding all these equations and cancelling the terms on the Left Hand side, we get,

(n+1)⁴–1⁴ = 4(1³ + 2³  + 3 ³ +  + n ³ ) + 6(1² + 2² + 3² +  + n² ) + 4(1 + 2 + 3 +  + n ) + n

n⁴ + 4n³ + 6n² + 4n = 4(1³ + 2³ + 3 ³ +  + n ³ ) + 6 ×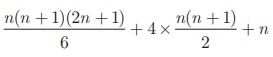 

4(1³ + 2³ + 3³ + â€¦ + n³ ) = n⁴    + 4n³ + 6n ² +4n − 2n³ −n² − 2n² − n − 2n² − 2n –n

4(1³ + 2³ + 3³ + â€¦ + n³ ) = n⁴    + 2n³ + n ² = n² (n² + 2n +1) = n²(n+1)²

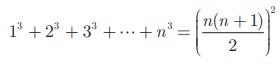
Ideal Friendship

Consider the numbers 220 and 284.

Sum of the divisors of 220 (excluding 220) = 1+2+4+5+10+11+20+22+44+55+110=284

Sum of the divisors of 284 (excluding 284) =1+2+4+71+142=220.

Thus, sum of divisors of one number excluding itself is the other. Such pair of numbers is called Amicable Numbers or Friendly Numbers.

220 and 284 are least pair of Amicable Numbers. They were discovered by Pythagoras. We now know more than 12 million amicable pair of Numbers.

Think Corner:  1. How many squares are there in a standard chess board? 2. How many rectangles are there in a standard chess board?

Here is a summary of list of some useful summation formulas which we discussed.

These formulas are used in solving summation problems with finite terms.

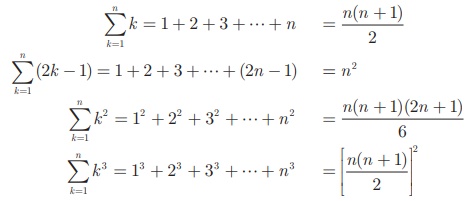
Example 2.54

Find the value of (i) 1 + 2 + 3 + ... + 50 (ii) 16 + 17 + 18 + ... + 75

Solution

(i) 1+ 2 + 3 +  + 50

Using, 1 + 2 + 3 +  + n =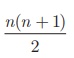 

 1+ 2 + 3 +  + 50  =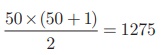 

(ii)  16 + 17 + 18 +  + 75  = (1 + 2 + 3 +  + 75) −(1 + 2 + 3 +  + 15) 

=75(75 + 1)/2 _− 15(15 + 1) / 2

=2850 −120 = 2730

Example 2.55

Find the sum of

(i) 1 + 3 + 5 + â€¦ + to 40 terms

(ii) 2 + 4 + 6 + â€¦ + 80

(iii) 1+3 + 5 + â€¦ + 55

Solution

(i) 1+3 + 5 +… 40 terms = 40²  = 1600

(ii) 2 + 4 + 6 + … + 80 = 2(1 + 2 + 3 + … + 40) = 2 × [40 × (40 + 1)]/2 = 1640

(iii) 1 + 3 + 5 + â€¦  + 55

Here the number of terms is not given. Now we have to find the number of terms using the formula, n = (l-a)/d + 1 gives n= [(55-1)/2] + 1 = 28

Therefore, 1 + 3 + 5 +  + 55 = (28)²  = 784

Example 2.56

Find the sum of  

(i) 1² + 2² +  + 19²

(ii) 5² + 1 0² + 15² +  + 105² 

(iii) 15² + 16² + 17 ² +  + 28²

Solution

Example 2.57

Find the sum of (i) 1³ + 2³ + 3³ +  + 16³ (ii) 9³ + 10³ +  + 21³ 

Solution

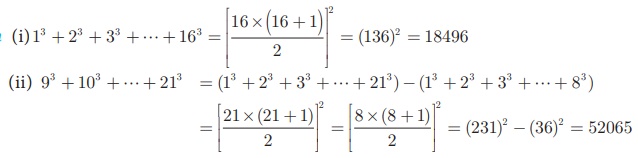
Example 2.58 If 1 + 2 + 3 + â€¦  + n = 666 then find n.

Solution 

Since, 1 + 2 + 3 + ... + n = 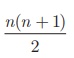, we have 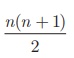= 666

n ² + n −1332 = 0  gives (n + 37 )(n − 36) = 0

So, n = −37 or n = 36

But n ≠ −37 (Since n is a natural number);

Hence n = 36.

Progress Check

Say True or False. Justify them.

·            The sum of first n odd natural numbers is always an odd number.

·            The sum of consecutive even numbers is always an even number.

·            The difference between the sum of squares of first n natural numbers and the sum of first n natural numbers is always divisible by 2.

·            The sum of cubes of the first n natural numbers is always a square number.