Example, Solution | Mathematics - Series: Sum to n terms of an A.P.(Arithmetic Progression) | 10th Mathematics : UNIT 2 : Numbers and Sequences
Chapter: 10th Mathematics : UNIT 2 : Numbers and Sequences
Series: Sum to n terms of an A.P.(Arithmetic Progression)
Series
The sum of the terms of
a sequence is called series. Leta1, a2, a3,...,
an ,... be the sequence of real numbers. Then the real number
a1 + a2 + a3 + is defined as the series of real numbers.
If a series has finite
number of terms then it is called a Finite series. If a series has infinite number of terms then
it is called an Infinite series. Let us focus our attention only on studying finite series
Sum to n terms of an A.P.
A series whose terms are
in Arithmetic progression is called Arithmetic series.
Let a , a
+ d , a + 2d , a + 3d,... be the Arithmetic
Progression.
The sum of first n
terms of a Arithmetic Progression denoted by Sn is given by,
Sn=a +(a + d )
+(a + 2d ) + + (a +(n −1)d )
…….(1)
Rewriting the above in
reverse order
Sn =(a +(n −
1)d) +(a + (n −2)d ) + +(a + d
) +a ..(2)
Adding (1) and (2) we
get,
2S n =[a +a + (n −1)d ]+[ a +d +a +(n − 2)d ] + … + [a +(n
− 2)d
+(a
+d )]+[a
+ (n
−1)d +a]
= [2a +(n
− 1)d
] +[2a + (n
−1)d
+ .. .. +[2a + (n −1)d
] (n
terms)
2Sn= n ×[2a + (n
−1)d
] gives Sn = n/2
[2a + (n − 1)d ]
Note
If the first term a,
and the last term l (nth term) are
given then

Example 2.31 Find the sum of first 15 terms of the A. P. 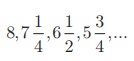
Solution
Here the first term a = 8, common difference d
= 
Sum of first n terms of an A.P.
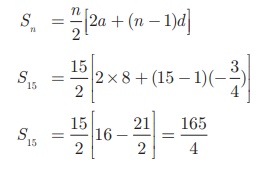
Example 2.32
Find the sum of 0. 40 + 0. 43 + 0. 46 + + 1 .
Solution
Here the value of n is not given. But the
last term is given. From this, we can find the value of n.
Given a = 0. 40
and l = 1 , we find d= 0. 43 −
0.40 = 0. 03 .
Therefore,

Sum of first n
terms of an A.P. Sn = 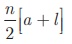
Here, n = 21
. Therefore, 
So, the sum of 21 terms
of the given series is 14.7.
Example 2.33
How many terms of the
series
1 + 5 + 9 + ... must be taken so that
their sum is 190?
Solution
Here we have to find the
value of
n, such that Sn = 190.
First term a = 1,
common difference d = 5 −1 = 4 .
Sum of first n
terms of an A.P.

But n = 10 as n
= −19/2 is impossible. Therefore, n = 10 .
State True or False.
Justify it.
1. The nth
term of any A.P. is of the form pn+q where p and q
are some constants.
2. The sum to nth
term of any A.P. is of the form pn2+qn + r
where p, q, r are some constants.
Example 2.34
The 13th term of an A.P. is 3 and the sum of first 13 terms is 234. Find the common difference and
the sum of first 21 terms.
Solution
Given the 13th term = 3 so, t13 = a + 12d = 3 .........
Sum of first 13 terms =
234 gives S 13 = 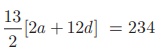
2a + 12d = 36 .........
Solving (1) and (2) we get, a = 33, d
= −5 /2
Therefore, common
difference is -5/2
Sum of first 21 terms = S21
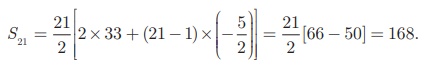
Example 2.35
In an A.P. the sum of
first n terms is 5n2/2 + 3n/2 . Find the 17th term.
Solution The 17th term can be obtained by
subtracting the sum of first 16 terms from the sum of first 17 terms.
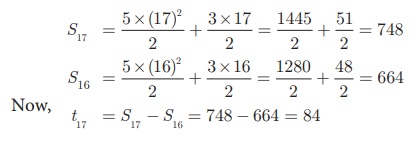
Example 2.36
Find the sum of all
natural numbers between 300 and 600 which are divisible by 7.
Solution
The natural numbers
between
300 and 600 which are divisible by 7 are 301, 308, 315, …, 595.
The sum of all natural
numbers between 300 and 600 is 301 + 308 + 315 + + 595.
The terms of the above
series are in A.P.
First term a =
301 ; common difference d = 7 ; Last term l = 595.
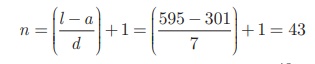
Since, Sn
= n/2 [a +l ] , we have S57 = 43/2
[ 301 + 595]= 19264.
Example 2.37
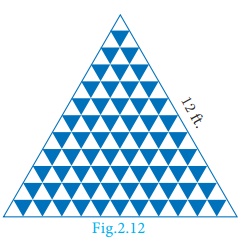
A mosaic is designed in
the shape of an equilateral triangle, 12 ft on each side. Each tile in the mosaic
is in the shape of an equilateral triangle of 12 inch side. The tiles are
alternate in colour as shown in the figure. Find the number of tiles of each
colour and total number of tiles in the mosaic.
Solution
Since the mosaic is in the shape of an equilateral triangle of 12 ft, and the tile is in the shape of an equilateral triangle of 12 inch (1 ft), there will be 12 rows in the mosaic
From the figure, it is
clear that number of white tiles in each row are 1, 2, 3, 4, …, 12 which
clearly forms an Arithmetic Progression.
Similarly the number of
blue tiles in each row are 0, 1, 2, 3, …, 11 which is also an Arithmetic
Progression.
Number of white tiles =
1 + 2 + 3 + … + 12 = 12/2
[1 + 12] = 78
Number of blue tiles = 0
+ 1 + 2 + 3 + … + 11 = 12/2 [0 + 11] = 66
The total number of
tiles in the mosaic = 78 + 66 = 144
Example 2.38
The houses of a street
are numbered from 1 to 49. Senthil’s house is numbered such that the sum of numbers of the
houses prior to Senthil’s house is equal to the sum of numbers of the houses
following Senthil’s house. Find Senthil’s house number?
Solution
Let Senthil’s house
number be x.
It is given that

x2 =2450 −x 2
− x ⇒ 2x 2 = 2450
x2 =1225 gives x =
35
Therefore, Senthil’s
house number is 35.
Example 2.39
The sum of first n, 2n and 3n terms of an A.P. are S1 ,S2 and S3 respectively.
Prove that S3
= 3(S2 −S1 ).
Solution
If S1 ,S2 and S3 are sum of first n, 2n and 3n terms of an A.P.
respectively then
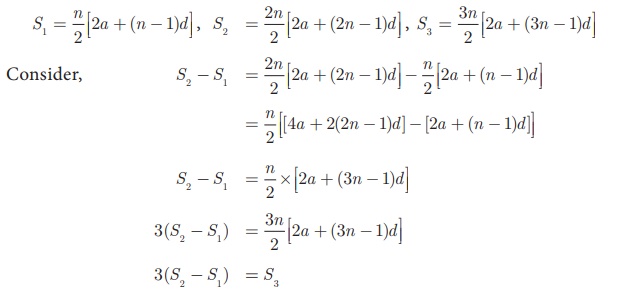
Related Topics