Structural Analysis: Flexibility Method

FLEXIBILITY METHOD

INTRODUCTION

These are the two basic methods by which an indeterminate skeletal structure is analyzed. In these methods flexibility and stiffness properties of members are employed. These methods have been developed in conventional and matrix forms. Here conventional methods are discussed.

suitable number of releases. The number of releases required is equal to staticalindeterminacy s. Introduction of releases results in displacement discontinuities at these releases under the externally applied loads. Pairs of unknown biactions (forces and moments) are applied at these releases in order to restore the continuity or compatibility of structure.

The computation of these unknown biactions involves solution of_? linear simultaneous equations. The number of these equations is equal to staticalindeterminacy s. After the unknown biactions are computed all the internal forces can be computed in the entires tructure using equations of equilibrium and free bodies of members. The required displacements can also be computed using methods of displacement computation.

Inflexibility methods inceunknowns are forces at the releases the method is also called force method. Since computation of displacement is also required at releases for imposing conditions of compatibility the method is also called compatibility method. In computation of displacements use is made of flexibility properties, hence, the method is also called flexibility method.

EQUILIBRIUM and COMPATABILITY CONDITIONS

Thethreeconditionsofequilibriumarethesumofhorizontalforces,verticalforcesandmom ents at anyjoint should beequal to zero.

i.e.?H=0;?V=0;?M=0

Forces should be in equilibrium

i.e.?F_X=0;?F_Y=0;?F_Z=0 i.e.?M_X=0;?M_Y=0;?M_Z=0

Displacement of a structure should be compatable

The compatibility conditions for the supports can be given as

1.Roller Support ?V=0 2.Hinged Support ?V=0, ?H=0

3.Fixed Support ?V=0, ?H=0, ??=0

DETERMINATE AND INDETERMINATE STRUCTURAL SYSTEMS

If skeletal structure is subjected to gradually increasing loads, without distorting the initial geometry of structure, that is, causing small displacements, the structure is said to be stable. Dynamic loads and buckling or instability of structural system are not considered here. Ifforthestable structure it is possible to find the internal forces in all the members constituting the structure and supporting reactions at all the supports provided from statically equations of equilibrium only, the structure is said to be determinate.

If it is possible to determine all the support reactions from equations of equilibrium alone the structure is said to be externally determinateelse externally indeterminate. If structure is externally determinatebutitis not possible to determine all internal forces then structure is said to be internally indeterminate. There foreastructural system may be:

(1)Externally indeterminate but internally determinate

(2)Externally determinate but internally indeterminate

(3)Externally and internally indeterminate

(4)Externally and internally determinate

 DETERMINATEVs INDETERMINATESTRUCTURES.

Determinate structures can be solving using conditions of equilibrium alone (?H=0;?V=0 ;?M=0). No other conditions are required.

Indeterminate structures cannot be solved using conditions of equilibrium because (?H?0; ?V?0;?M?0). Additional conditions are required for solving such structures. Usually matrix methods are adopted.

INDETERMINACYOF STRUCTURAL SYSTEM

The indeterminacy of a structure is measured as statically (?_s) or kinematical (?k) Indeterminacy.

?_s= P (M - N + 1) - r = PR- r ?_k= P (N - 1) + r - s+?k= PM -c P = 6 for space frames subjected to general loading

P = 3 for plane frames subjected to inplane or normal to plane loading. N = Numberof nodes in structural system.

M=Numberofmembersofcompletelystiffstructurewhichincludesfoundationas singly connected system of members.

Incompletely stiff structure thereisnorelease present. In singly connected system of rigid foundation members there is only one route between any two points  in which tracks are not retraced. The system is considered comprising of closed rings or loops.

R = Number of loops or rings in completely stiff structure. r = Number of releases in the system.

c = Number of constraints in the system. R = (M - N + 1)

For plane and space trusses ?_sr  educes ^to:?_s=M- (NDOF)N+ P

M= Number of members in completely stifftruss.

P = 6 and 3 for space and plane truss respectively

N= Number of nodes in truss.

NDOF = Degrees of freedomat node which is 2 for plane truss and 3 for space truss. For space truss?_s=M- 3N+ 6

For plane truss?_s= M- 2 N+ 3

Test for static indeterminacy of structural system

If ?_s> 0 Structure is statically indeterminate

If ?_s= 0 Structure is statically determinate

and if?_s<0 Structure is a mechanism.

It may be noted that structure may be mechanism even if ?_s >0 if thereleases are present in such away so as to cause collapse as mechanism. The situation of mechanism is unacceptable.

Statically Indeterminacy

It is difference of the unknown forces (internal forces plusexternal reactions) and the equations of equilibrium.

Kinematic Indeterminacy

It is the number of possible relative displacement softhenodes in the directions of stress resultants.

PRIMARY STRUCTURE

A structure formed by the removing the excess or redundant restraints from an indeterminate structure making it statically determinate is called primary structure. This is required for solving indeterminate structures by flexibility matrix method.

Indeterminate structure         Primary Structure

ANALYSIS OF INDETERMINATE STRUCTURES :BEAMS

1Introduction

·          Solve  statically indeterminate beams of degree more than one.

·          To solve the problem in matrix notation.

·          To compute reactions at all the supports.

·        To compute internal resisting bending moment at any section of the continuous beam.

Beams which are statically indeterminate to first degree, were considered. If the structure is statically indeterminate to a degree more than one, then the approach presented in the force method is suitable.

Problem 1.1

Calculate the support reactions in the continuous beam ABC due to loading as shown in Fig.1.1 Assume EI to be constant throughout.

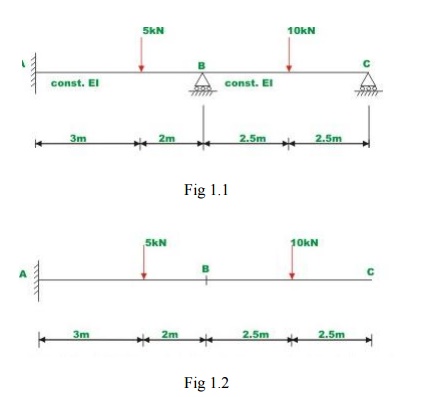
Select two reactions vise, at B(R1 ) and C(R2 ) as redundant, since the given beam is statically indeterminate to second degree. In this case the primary structure is a cantilever beam AC. The primary structure with a given loading is shown in Fig. 1.2

In the present case, the deflections (? L)1 and (? L) 2 of the released structure at B and C can be readily calculated by moment-area method. Thus

(? L) 1        = ? 819.16 / EI    

(? L) 2        = ? 2311.875/ EI  (1)

For the present problem the flexibility matrix is,

a11= 125/3EI ,a21= 625/6EI  

a12= 625/6EI , a22 = 1000/3EI        (2)

In    the   actual   problem   the   displacements   at B and Care  zero. Thus the

compatibility conditions for the problem may be written as, a11 R1+ a12 R2 + (? L) 1 = 0

a21 R1+ a22 R2+ (? L) 2  = 0(3)

Substituting the value of E and I in the above equation,

R1 = 10.609 KN and R2 = 3.620 KN

Using equations of static equilibrium, R3 = 0.771  KN m and R4  = ?0.755KN m

Problem 1.2

A Fixed beam AB of constant flexural rigidity is shown in Fig.1.3 The beam is subjected to auniform distributed load of w moment M=wL² kN.m. Draw Shear force and bending moment diagrams by force method.

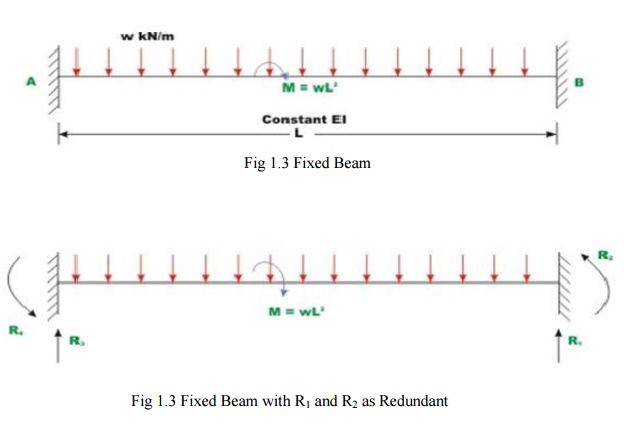
Fig 1.3 Fixed Beam with R1 and R2 as Redundant

Select vertical reaction (R1)and the support moment(R2) at    B as the redundant. The primary structure in this case is acantilever beam which could  be obtained by releasing the redundant  R1  andR2.  

The R1 is assumed to  positive in the upward direction and R2   is assumed to be positive in the counterclockwise direction. Now, calculate deflection at B duetoonly applied loading. Let (  L ) be the transverse deflection at1 B and(  L  2 bethe  slope at B  due to external loading. The positive directions of the selected redundant are shown in Fig.8.3b.

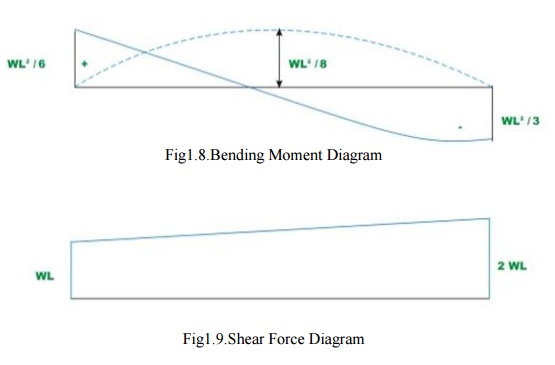
The deflection(? L₁)and(? L₂)of the released structure can be evaluated from unit load method. Thus,

(? L₁) =wL⁴/8EI - 3wL⁴/8EI = ?wL⁴/2EI - (1)

(? L₂) = wL³/6EI - wL³  /2EI = ? 2wL³/3EI   --- -(2)

The negative sign indicates that ( L )is downwards and rotation( is   1 L2) clockwise. 

Problem 1.3.

A continuous beam ABC is carrying a uniformly distributed load of 1 kN/m in addition to a concentrated load of 10kN as shown in Fig.7.5a, Draw bending moment and shear force diagram. Assume EI to be constant for all members.

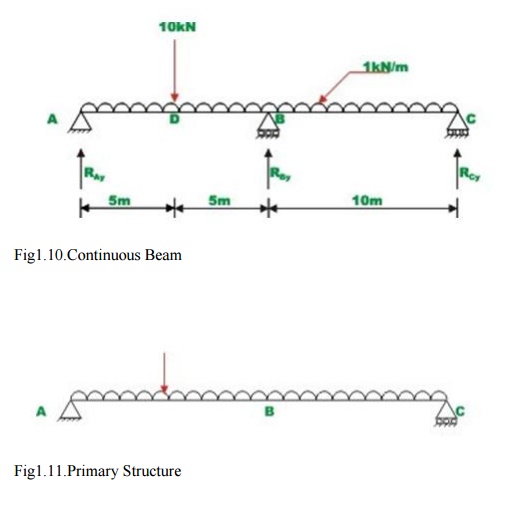
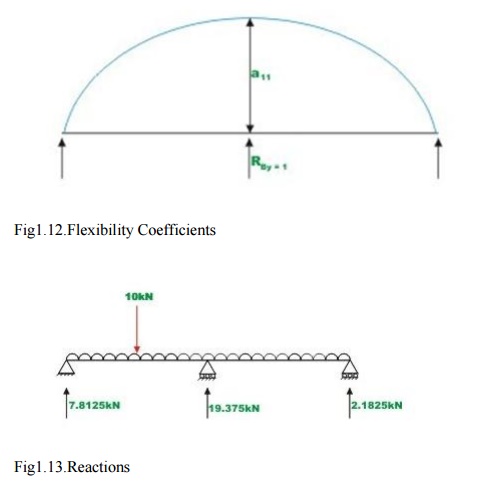
It is observed that the continuous beam is statically indeterminate to first degree. Choose the reaction at B, R_By as the redundant. The primary structure is a simply supported beam as shown in Fig.1.11. Now, compute the deflection at B, in the released structure due to uniformly distributed load and concentrated load. This is accomplished by unit load method. Thus,

In thenextstep, apply a unit load at B in the direction of

R_By(upwards)and

Calculate the deflection at B of the following structure. Thus(seeFig.7.5c),

Now, deflection at B in the primary structure due to redundant       R_B  is,

In the actual structure, the deflection at B is zero. Hence, the compatibility equation may be written as

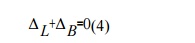
_L+  _B=0(4)

The other two reactions are calculated by static equilibrium equations (videFig.

1.13)

R_A =7.8125kN

R_B =2.8125kN