Chapter: Civil : Structural Analysis : Flexibility Method
Important Questions and Answers:Flexibility Matrix Method For Indeterminate Structures
FLEXIBILITYMATRIXMETHOD
FORINDETERMINATE STRUCTURES
1. What
is meant by indeterminate structures?
Structures that do not satisfy the conditions of equilibrium
are called indeterminate structure. These structures cannot be solved by ordinary
analysis techniques.
2. What are the
conditions of equilibrium?
The three conditions of equilibrium are the sum of horizontal forces,
vertical forces and moment sat any joint should be equal to zero.
i.e. ?H=0;?V=0;?M=0
3. Differentiate
between determinate and indeterminate structures.
Determinate structures can be solving using conditions of equilibrium
alone (?H=0;?V =0;?M=0). No
other conditions are required. Indeterminate structures cannot be solved using conditions
of equilibrium because (?H? 0;?V?0;?M?0). Additional
conditions are required for solving such structures. Usually matrix methods are
adopted.
4. Define degree
of indeterminacy (i).
The excess number of reactions that make a structure indeterminate
is called degree of indeterminacy, and is denoted by (i).Indeterminacy is also called
degree of redundancy. Indeterminacy consists of internal and external
indeterminacies.
i =II+EI
where II=internal indeterminacy
and EI=external indeterminacy.
5. Define internal
and external indeterminacies.
Internal indeterminacy(II) is the excess no of internal forces
present in a member that make a structure indeterminate.
External indeterminacy(EI) is excess no of external reactions in
the member that make the structure indeterminate.
i =II+EI;
EI=r- e;
Where r=no of support reactions and
e=equilibrium conditions II=i -EI
e=3 (plane frames) and
e=6 (space frames)
6. Write
the formulae for degree of indeterminacy for:
(a)Two
dimensional pin jointed truss(2D Truss)
i = (m+r) - 2j where m=no of members
r=no of reactions
j
=no of joints
(b)Two dimensional rigid frames/plane rigid frames (2DFrames)
i
=(3m+r)- 3j
where
m=no ofmembers
r=no of reactions
j =no ofjoints
(c)Three dimensional space truss (3D Truss)
i = (m+r)- 3j where
m=no of members
r=no of reactions
j
=no of joints
(d)Three dimensional space frames (3DFrame)
i =(6m+r)- 6j
where m=no of members
r=no of reactions
j
=no of joints
7. Determine the degree of indeterminacy for the
following 2D truss. i =(m+r)-2j
Where m=19
r=4
j =10 e=3
?i =(19+4)-2x10=3
External indeterminacy EI=r-e=4-3=1
?Internal indeterminacy II=i-EI=3-1=2

8. Determine the total, internal
and external degree of indeterminacy for the plane rigid frame below.
i =(3m + r)- 3j
where m=7
r=4 j =6 e=3
?i =(3x7+
4)-
(3x6)
=7
External indeterminacy EI=r-e=4-3=1
?Internal indeterminacy II=i-EI=7-1=6
9. Determine i, EI, II for the given plane
truss. i =(m + r)- 2j
Where
m=3 r=4 j =3 e=3
?i =(3+ 4)-(2x3) =1
External indeterminacy EI=r-e=4-3=1
?Internal indeterminacy II=i-EI=1-1=0
10. Find the indeterminacy for the beams given below.
For beams degree of indeterminacy is given by i
=r-e
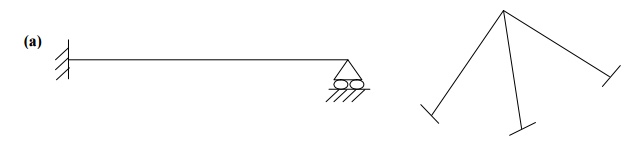
i =r-e
where
r=no of reactions, e=no of equilibrium conditions r=4 and e=3
?i =4-3=1

i =r-e
where
r=5 and e=3
?i =5-3=2
11. Find the indeterminacy for the given rigid
plane frame. i =(3m + r)- 3j
Where
m=3
r=4 j =4
?i =(3x3+
4)-
(3x4)
=1
External indeterminacy EI=r-e=4-3=1
?Internal indeterminacy II=i-EI=1-1=0
12. Find the indeterminacy of the space rigid
frame. i =(6m + r)- 6j
Where
m=8
r=24 (i. e. 6persupportx4) j =8 e=6
?i
=(6x8+24)- (6x 8) =24
External indeterminacy EI=r-e=24-6=18
?Internal
indeterminacy II=i-EI=24-18=6
13. Find the indeterminacy for the given space
truss. i =m +r-3j
Where m=3
r=18 (i. e. 6reactions persupport x3) j =4
?i =(3+18)-
(3x4)
=9
External indeterminacy EI=r-e=18-6=12
?Internal
indeterminacy II=i-EI=9-12=-3
14.
What are the different methods of analysis of
indeterminate structures.
The various methods adopted for the analysis of indeterminate structures
include:
(a) Flexibility
matrix method.
(b) Stiffness matrix method
(c)Finite Element method
15. Briefly mention the two types
of matrix methods of analysis of indeterminate structures.
The two matrix methods of analysis of indeterminate structures
are: (a) Flexibility matrix method- This
method is also called the force method in which the forces in the structure are
treated as unknowns. Then o of equations involved is equal to the degree of static
indeterminacy of the structure.
(b)Stiffness matrix method- This is
also called the displacement method in which the displacements that occur in
the structure are treated as unknowns. Then o of displacements involved is
equal to then o of degrees of freedom of the structure.
16.
Define a primary structure.
A structure formed by the removing the excess or redundant
restraints from an indeterminate structure making it statically determinate is
called primary structure. This is required for solving indeterminate structures
by flexibility matrix method.
17.
Give the primary structures for the following
indeterminate structures.
Indeterminate structure Primary Structure
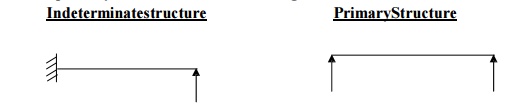
18. Define kinematic indeterminacy (Dk) or Degree of Freedom
(DOF)
Degrees of freedom is defined as the least no of independent
displacements required to define the deformed shape of a structure. There are two
types of DOF: (a)Nodal type DOF and (b)Joint type DOF.
19. Briefly explain the two types of DOF.
(a)Nodal type DOF- This
includes the DOF at the point of application of concentrated load or moment, at
a section where moment of inertia changes, hinge support, roller support and
junction of two or more members.
(b)Joint type DOF- This
includes the DOF at the point where moment of inertia changes, hinge and roller
support, and junction of two or more members.
20. For the various support conditions shown
below give the DOFs.
(a) No
DOF
(b) 1-
DOF
(c) 2-
DOF
(d) 1-
DOF
21. For the truss shown below, what
is the DOF?
Pin
jointed plane frame/truss
DOF/ Dk = 2j-r
where r=no of reactions
j = no of
joints
22.
Define compatibility in force method of analysis.
Compatibility is defined as the continuity condition on the displacements
of the structure after external loads are applied to the structure.
23.
Define the Force Transformation Matrix.
The connectivity matrix which relates the internal forces Q
and the external forces R is known as the force transformation matrix. Writing it
in a matrix form,
{Q} =[b]{R}
where Q=member force matrix/vector
b= force transformation
matrix
R =
external force/load matrix/ vector
24.
What are the requirements to be satisfied
while analyzing a structure?
The three conditions to be satisfied are:
(a)Equilibrium condition
(b)Compatibility condition
(c)Force displacement condition
25. Define flexibility influence coefficient(fij)
Flexibility influence coefficient (fij) is defined
as the displacement at joint 'i' due to a unit load at
joint 'j', while
all other joints are not load.
26.
Write theelementflexibility matrix(f)fora
truss member.
The element flexibility matrix(f) for a truss
member is given

Related Topics