Chapter: Civil : Structural Analysis : Stiffness Matrix Method
Structural Analysis: Stiffness Matrix Method
STIFFNESS MATRIX METHOD
INTRODUCTION
The given indeterminate structure is first made kinematic
ally determinate by introducing constraints atthenodes. The required number of constraints
is equal to degrees of freedom at the nodes that is kinematic indeterminacy ?k. The kinematic
ally determinate structure comprises of fixed ended members, hence, all nodal
displacements are zero. These results in stress resultant discontinuities at these
nodes under the action of applied loads or in other words the clamped joints are
not in equilibrium.
Inorder to restore the equilibrium of stress resultants
at the nodes the nodes are imparted suitable unknown displacements. The number of
simultaneous equations represen ting joint equilibrium of forces is equal to kinematic
indeterminacy ?k. Solution of these equations gives unknown nodal
displacements. Using stiffness properties of members the memberend forces are computed
and hence the internal forces through out the structure.
Since nodal displacements are unknowns, the method
is also called displacement method. Since equilibrium conditions are applied at the joints
the method is also called equilibrium method. Since stiffness properties of members
are used the method is also called stiffness method.
In the displacement method of
analysis the equilibrium equations are written by expressing the unknown joint displacements
in terms of loads by using load-displacement relations. The unknown joint displacements
(the degrees of freedom of the structure) are calculated by solving equilibrium
equations. The slope -deflection and moment - distribution methods were extensively
used before the high speed computing era. After the revolution in computer industry,
only direct stiffness method is used.
PROPERTIES OFTHESTIFFNESS MATRIX
The properties of the stiffness matrix are:
·
It is asymmetric matrix
·
The sum of elements in any column must be equal to
zero.
·
It is an unstable element therefore the determinant
is equal to zero.
ELEMENT AND GLOBAL STIFFNESS MATRICES
Local co ordinates
In the analysis for convenience
we fix the element coordinates coincident with the member axis called element
(or) local coordinates (coordinates defined along the individual member axis )
Global co ordinates
It is normally necessary to define a coordinate
system dealing with the entire structure is called system on global coordinates
(Common coordinate system dealing with the entire structure)
Transformation
matrix
The connectivity matrix which relates the internal forces Q
and the external forces R is known as the force transformation matrix. Writing it
in a matrix form,
{Q}
=[b]{R}
Where Q=member force matrix/vector, b=force transformation
matrix R = external force/load matrix/ vector
ANALYSIS OF CONTINUOUS BEAMS
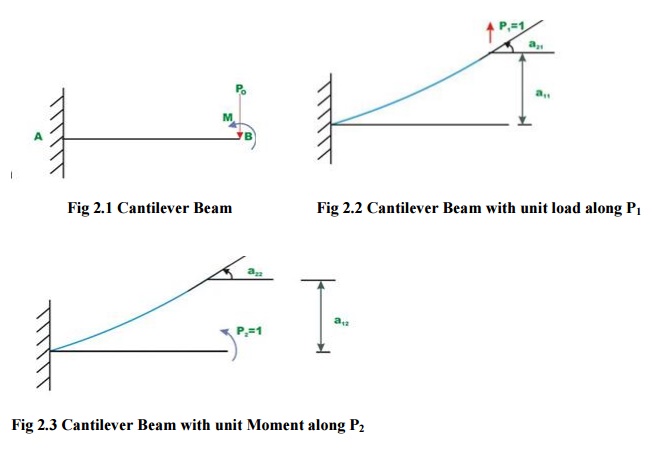





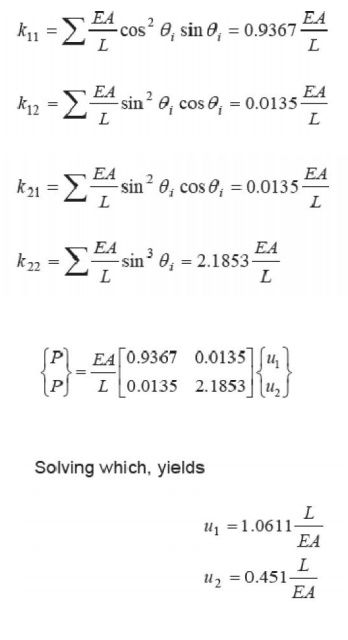
ANALYSIS OF PIN JOINTED PLANE FRAMES
An introduction to the stiffness method was given in
the previous Page. The basic principles involved in the analysis of beams, trusses
were discussed. The problems were solved with hand computation by the direct application
of the basic principles. The procedure discussed in the session (page) though enlighteningarenot suitable for computer
programming. It is necessary to keesphand computation to a minimum while implementing
this procedure on the computer.
In this session a formal approach has been discussed which may be readily
programmed on a computer. In this
less on the direct stiffness method as applied to planar truss structure is discussed.
Planetrusses are made up of short thin members inter connected
a thin gesto form triangulated patterns. Ahinge connection can only transmit forces
from one member to another member but not the moment. For analysis purpose, the truss is loaded at the joints. Hence,
a truss member is subjected to only axial forces and the forces remain
constant along the length of the member. The forces in the member at its two
ends must be of the same magnitude but actin the opposite directions for
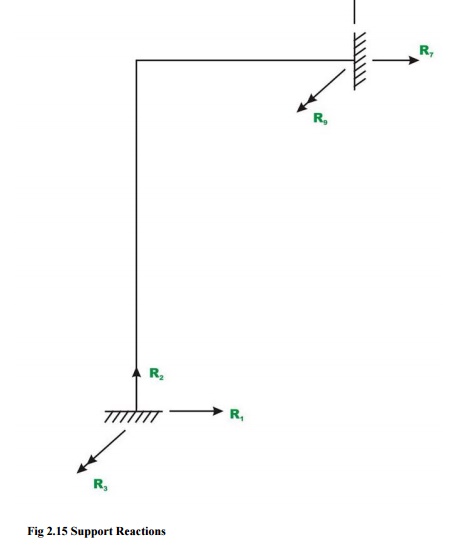
equilibrium as shown in Fig.2.8



STIFFNESS
MATRIX METHOD
1. What are
the basic unknowns in stiffness matrix method?
In the stiffness matrix method nodal displacements are treated
as the basic unknowns for the solution of indeterminate structures.
2. Define
stiffness coefficient kij.
Stiffness coefficient 'kij' is defined as
the force developed at joint 'i' due to unit
displacement at joint 'j' while all other joints are fixed.
3. What is
the basic aim of the stiffness method?
The aim of the stiffness method is to evaluate the values of generalized
coor dinates 'r' knowing the structure stiffness matrix 'k' and
nodal loads 'R' through the structure equilibrium
equation.
{R}
=[K]{r}
4. What is
the displacement transformation matrix?
The connectivity matrix which relates the internal displacement
'q'
and
the external displacement 'r'
is known
as the displacement transformation matrix 'a'.
{q}
=[a]{r}
5. How are
the basic equations of stiffness matrix obtained?
The basic equations of stiffness matrix are obtained
as:
·Equilibrium forces
·Compatibility
of displacements
·Force displacement
relationships
6. What is
the equilibrium condition used in the stiffness method?
The external loads and the internal member forces must be in
equilibrium at the nodal points.
7. What is
meant by generalized coordinates?
For specifying a configuration of a system, a certain minimum
no of indepen dent coordinates are necessary. The least no of independent
coordinates that are needed to specify the configuration is known as
generalized coordinates.
8. What is
the compatibility condition used in the flexibility method?
The deformed elements fit together at nodal points.
9. Write about
the force displacement relationship.
The relationship of each element must satisfy the stress-strain
relationship of the element material.
10.
Write the element stiffness for a truss
element.
The element stiffness matrix for a truss element
is given by

11.
Write the element stiffness matrix for a beam
element.
The element stiffness matrix for a beam element is
given by
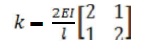
12.
Compare flexibility method and stiffness
method.
Flexibility matrix method
·The redundant forces are treated as basic unknowns.
·The number of equations involved
is equal to the degree of static indete rminacy of the structure.
·The method is the generalization
of consistent deformation method. ·Different
procedures are used for determinate and indeterminate structures
Stiffness
matrix method
·The joint displacements are treated
as basic unknowns
·The number of displacements
involved is equal to the no of degrees of freedom of the structure
·The method is the generalization
of the slope deflection method.
·The same procedure is used for both determinate and
indeterminate structures.
13.
Is it possible to develop the flexibility
matrix for an unstable structure?
In order to develop the flexibility matrix for a structure, it
has to be stable and determinate.
14.
What is the relation between flexibility and
stiffness matrix?
The element stiffness matrix 'k' is the inverse of the
element flexibility matrix 'f' and is given by f=1/k or k
=1/f.
15.
What are the type of structtures that can be solved
using stiffness matrix method?
Structures such as simply supported, fixed beams and portal
frames can be solved using stiffness matrix method.
16.
Give the formula for the size of the Global
stiffness matrix.
The size of the global stiffness matrix (GSM) =No: of nodes x Degrees
of free dom per node.
17.
List the properties of the stiffness matrix
The properties of the stiffness matrix are:
· It is a symmetric
matrix
· The sum
of elements in any column must be equal to zero.
· It is an
unstable element there fore the determinant is equal to zero.
18Why is
the stiffness matrix method also called equilibrium method or displacement
method?
Stiffness method is based on the superposition of displacements
and hence is also known as the dispalcement method. And since it leads to the
equilibrium equations the method is also known as equilibrium method.
19 If the flexibility matrix is given as

20 Write the n stiffness matrix for a 2D beam
element. The stiffness matrix for a 2 D beam element is given by

Related Topics