Solved Problems: Structural Analysis- Flexibility Method

Problem 1.1

Calculate the support reactions in the continuous beam ABC due to loading as shown in Fig.1.1 Assume EI to be constant throughout.

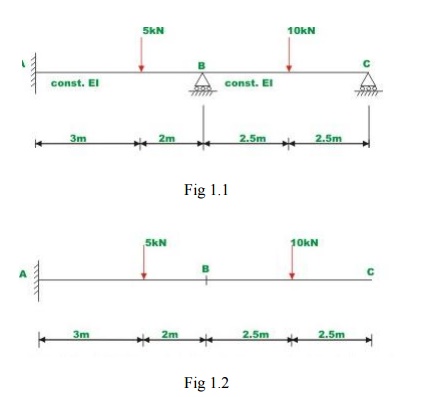
Select two reactions vise, at B(R1 ) and C(R2 ) as redundant, since the given beam is statically indeterminate to second degree. In this case the primary structure is a cantilever beam AC. The primary structure with a given loading is shown in Fig. 1.2

In the present case, the deflections (? L)1 and (? L) 2 of the released structure at B and C can be readily calculated by moment-area method. Thus

(? L) 1        = ? 819.16 / EI    

(? L) 2        = ? 2311.875/ EI  (1)

For the present problem the flexibility matrix is,

a11= 125/3EI ,a21= 625/6EI  

a12= 625/6EI , a22 = 1000/3EI        (2)

In    the   actual   problem   the   displacements   at B and Care  zero. Thus the

compatibility conditions for the problem may be written as, a11 R1+ a12 R2 + (? L) 1 = 0

a21 R1+ a22 R2+ (? L) 2  = 0(3)

Substituting the value of E and I in the above equation,

R1 = 10.609 KN and R2 = 3.620 KN

Using equations of static equilibrium, R3 = 0.771  KN m and R4  = ?0.755KN m

Problem 1.2

A Fixed beam AB of constant flexural rigidity is shown in Fig.1.3 The beam is subjected to auniform distributed load of w moment M=wL2 kN.m. Draw Shear force and bending moment diagrams by force method.

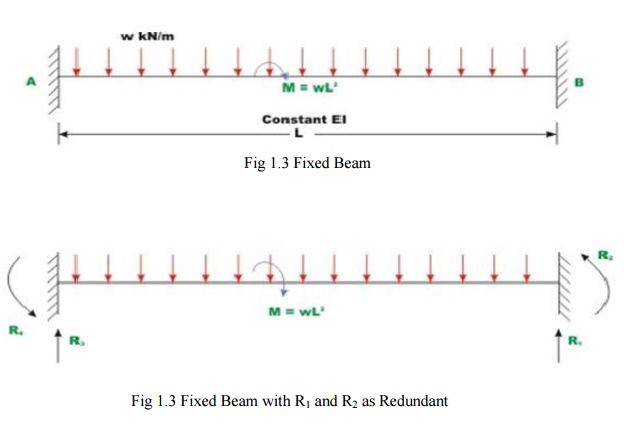
Fig 1.3 Fixed Beam with R1 and R2 as Redundant

Select vertical reaction (R1)and the support moment(R2) at    B as the redundant. The primary structure in this case is acantilever beam which could  be obtained by releasing the redundant  R1  andR2.  

The R1 is assumed to  positive in the upward direction and R2   is assumed to be positive in the counterclockwise direction. Now, calculate deflection at B duetoonly applied loading. Let (  L ) be the transverse deflection at1 B and(  L  2 bethe  slope at B  due to external loading. The positive directions of the selected redundant are shown in Fig.8.3b.

The deflection(? L1)and(? L2)of the released structure can be evaluated from unit load method. Thus,

(? L1) =wL4/8EI - 3wL4/8EI = ?wL4/2EI - (1)

(? L2) = wL3/6EI - wL3  /2EI = ? 2wL3/3EI   --- -(2)

The negative sign indicates that ( L )is downwards and rotation( is   1 L2) clockwise. 

Problem 1.3.

A continuous beam ABC is carrying a uniformly distributed load of 1 kN/m in addition to a concentrated load of 10kN as shown in Fig.7.5a, Draw bending moment and shear force diagram. Assume EI to be constant for all members.

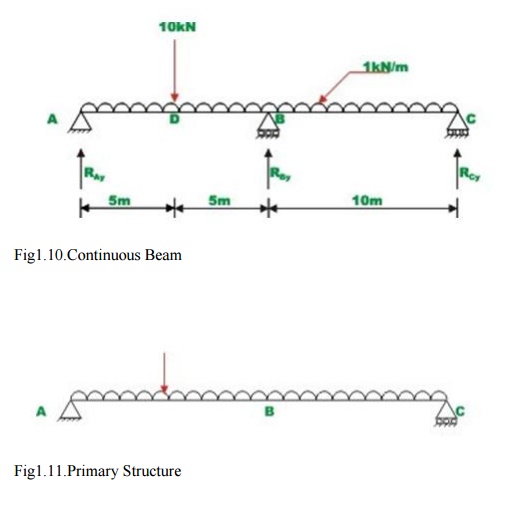
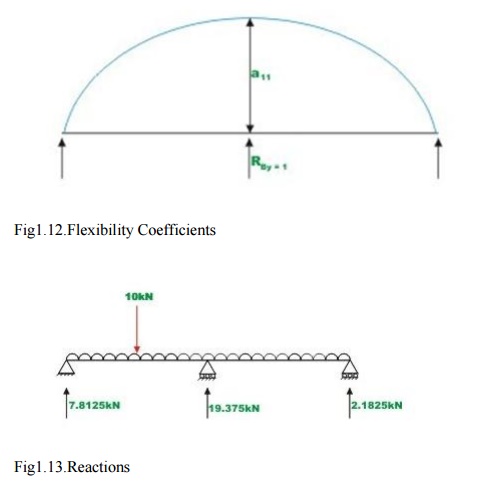
It is observed that the continuous beam is statically indeterminate to first degree. Choose the reaction at B, RBy as the redundant. The primary structure is a simply supported beam as shown in Fig.1.11. Now, compute the deflection at B, in the released structure due to uniformly distributed load and concentrated load. This is accomplished by unit load method. Thus,

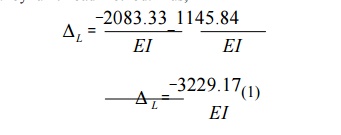
In thenextstep, apply a unit load at B in the direction of

RBy(upwards)and

Calculate the deflection at B of the following structure. Thus(seeFig.7.5c),

Now, deflection at B in the primary structure due to redundant       RB  is,

In the actual structure, the deflection at B is zero. Hence, the compatibility equation may be written as

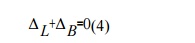
L+  B=0(4)

The other two reactions are calculated by static equilibrium equations (videFig.

1.13)

RA =7.8125kN

RB =2.8125kN