Chapter: Civil : Structural Analysis : Moment Distribution Method
Structural Analysis - Moment Distribution Method with Solved Problems
MOMENT DISTRIBUTION METHOD
INTRODUCTION
AND BASIC PRINCIPLES
Introduction
(Method
developed by Prof. Hardy Cross in 1932)
The method solves for the joint mo ments in continuous beams and rigid frames by successive approxi mation
Statement
of Basic Principles
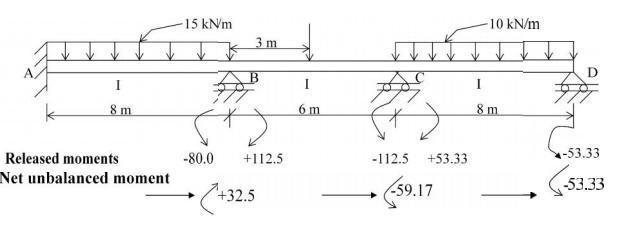
Consider
the continuous beam ABC D, subjected to the given loads,
as shown
in Figure below. Assume that only rotation of joints occur
at B, C
and D, and that no support d isplacements occur at B, C and
D. Due to the applied loads in spans AB, BC and
CD, rotations occur at B, C and D

In order to solve the problem in a su ccessively approximating
manner,
it can be visualized to be made up of a continued two-stage
problems
viz., that of locking and releasing the joints in a continuous
sequence.
The joints B, C and D are locked
in position before any load is applied on the b eam ABCD; then given loads are
applied on the bea m. Since the joints of beam ABCD are locke d in position,
beams AB, BC and CD acts as ind ividual and separate fixed beams, subjected to
the applied loads; these loads develop fixed ennd moments.
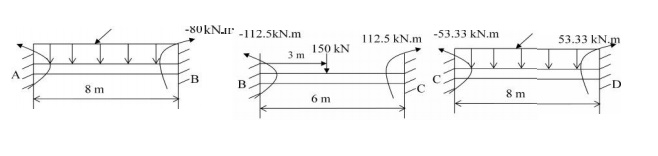
In beam AB
Fixed end moment at A = -wl2/12 = - (15)(8)(8)/12 =
- 80 kN.m
Fixed end moment at B = +wl2/12 = +(15)(8)(8)/12 =
+ 80 kN.m
In beam BC
Fixed end moment at B = - (Pab2)/l2 = -
(150)(3)(3)2/62
= -112.5
kN.m
Fixed end moment at C = + (Pab2)/l2 = +
(150)(3)(3)2/62
= + 112.5
In beam AB
Fixed end moment at C = -wl2/12 = - (10)(8)(8)/12 =
- 53.33 kN.m
Fixed end moment at D = +wl2/12 = +(10)(8)(8)/12
= + 53.33kN.m
Since the
joints B, C and D were fix ed artificially (to compute the the fixed-end
moments), now the joints B, C and D are released and allowed to rotate. Due to
the joint release, the joints rotate
maintaining the continuous nature of the beam. Due to the joint release, the
fixed en d moments on either side of joints B, C and D act in the opposite
direction now, and cause a net un balanced moment to occur at the joint.
These unbalanced moments act at th e joints and modify the
joint moments at B, C a nd D, according to their relative stiffnesses at the
respective joints. The joint moments are distributed t o either side of the
joint B, C or D, according to their reelative stiffnesses. These distributed
moments al so modify the moments at the opposite side of the beam span, viz.,
at joint A in span AB, at joints B and C in span BC and at joints C and D in
span CD. This modification is dependent on the carry-over factor (which is
equal to 0.5 in this case);
The carry-over moment becomes the unbalanced
moment at the joints to whic h they are carried over. Steps 3 and 4 are
repeated t ill the carry-over or distributed moment beco mes small.
Sum up
all the moments at each of the joint to obtain the joint moments.
SOME BASIC
DEFINITIONS
In order to understand the five steps mentioned in section
7.3, some words need to be defined and relevant derivations made.
1Stiffness
and Carry-over Factors
Stiffness
= Resistance offered by m ember to a unit displacement or rotation at a point,
for given support constraint conditions
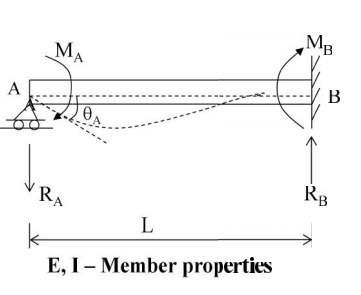
A clockwise moment MA is applied at A to produce a
+ve bending in beam AB. Fin d qA and MB.
Using
method of consistent defor mations

Considering moment MB,
MB
+ MA + RAL = 0
\MB = MA/2= (1/2)MA
Carry - over Factor = 1/2
2 Distribution Factor
Distribution
factor is the ratio according to which an externally applied unbalanced moment
M at a joint is apportioned to the various m embers mating at the joint
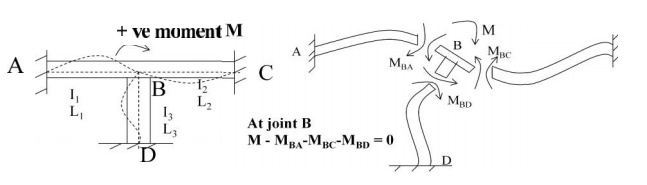
M = MBA
+ MBC + MBD
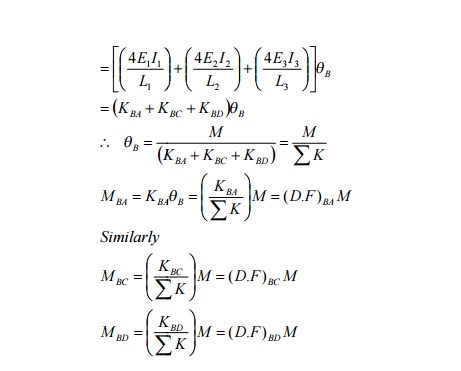
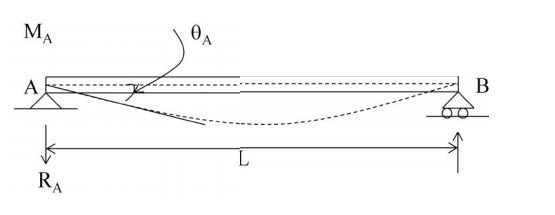
Modified Stiffness Factor
The
stiffness factor changes when t he far end of the beam is simply-supported.
As per
earlier equations for deforma tion, given in Mechanics of Solids text-books.
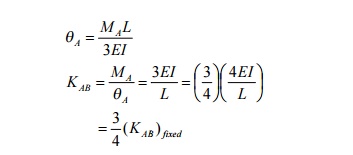
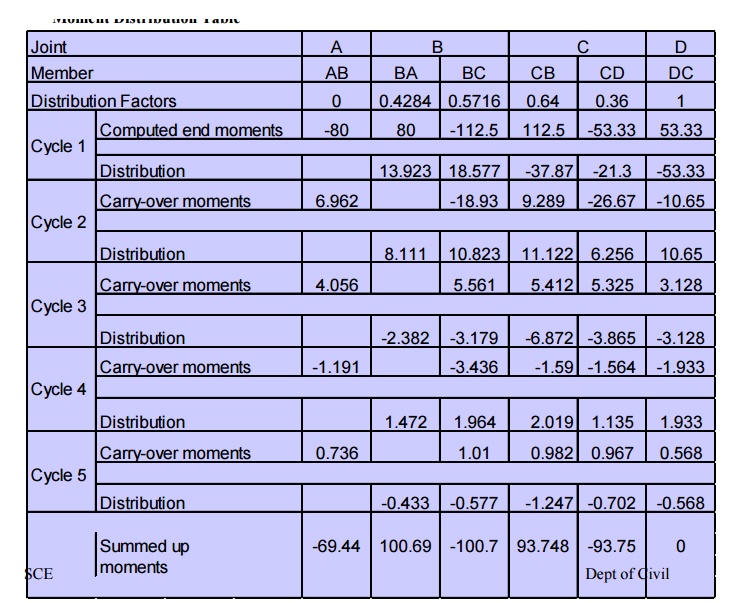
Solve the previously given proble m by the moment
distribution method
Fixed end
moments

Stiffness
Factors (Unmodified Stifffness
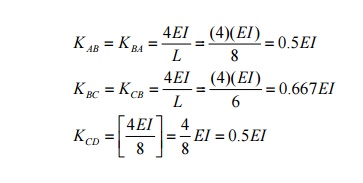
Distribution
Factors

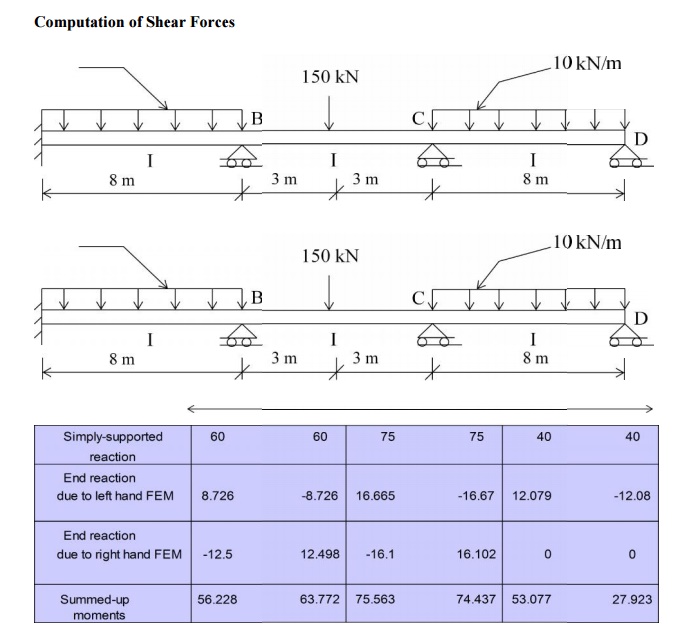
Computation
of Shear Forces
Related Topics