Chapter: Civil : Structural Analysis : Slope Deflection Method
Solved Problems: Slope Deflection Method- Structural Analysis
SLOPE DEFLECTION METHOD
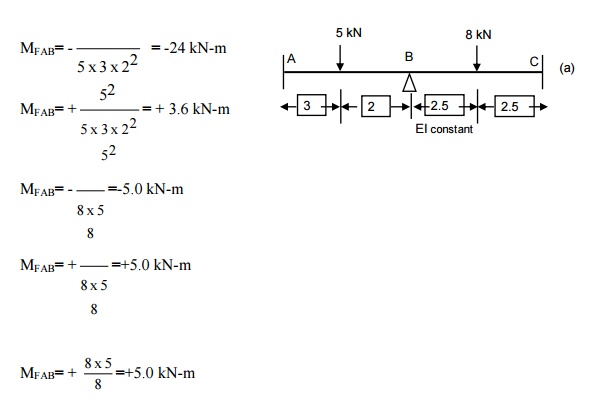
(1). A beam ABC, 10m
long, fixed at ends A and B is continuous over joint B and is loaded as shown
in Fig. Using the slope deflection method, compute the end moments and plot the
bending moment diagram. Also, sketch the deflected shape of the beam. The beam
has constant EI for both the spans.
Solution.
(a)
Fixed end moments
Treating each span as a fixed beam, the
fixed end moments are as follows:
(b)
Slope deflection equations
The end rotations qA and qC are zero since the
beam is fixed at A and C. hence there is only o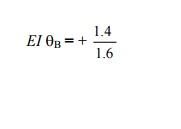 ne unknown, qB. the ends do not
settle and hence dfor each span is
zero. Let us assume qB
to be positive. The result will indicate the correct sign. The slope deflection
equations are as follows:
ne unknown, qB. the ends do not
settle and hence dfor each span is
zero. Let us assume qB
to be positive. The result will indicate the correct sign. The slope deflection
equations are as follows:
For span AB,
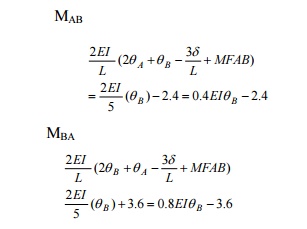
For span BC,
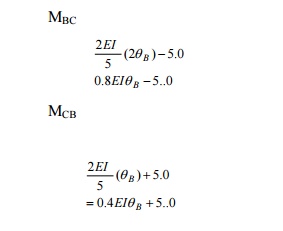
(c)
Equilibrium equation
Since there is only one
un known, i.e. qB,
one equilibrium equation is sufficient. For the joint B, we have
MBA + MBC = 0
\(0.8 EI qB + 3.6) + (0.8 EI
qB
+ 5.0) = 0 1.6 EI qB
= 1.4
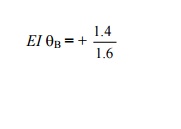
The plus sign indicates that qB is positive (i.e.
rotation of tangent at B is clockwise).
(d)
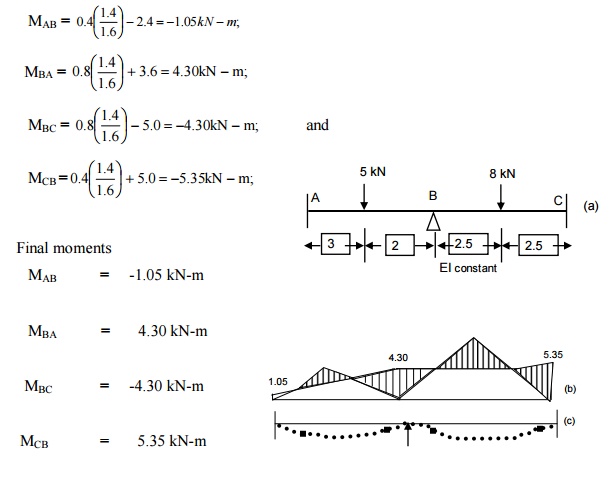
Final moments
Substituting the values of EI qB in Eqa. (1) to (4), we
get
(2) A beam ABC, 10m long, hinged at ends
A and B is continuous over joint B and is loaded as shown in Fig. Using the
slope deflection method, compute the end moments and plot the bending moment
diagram. Also, sketch the deflected shape of the beam. The beam has constant EI
for both the spans.
SOLUTIONS
(a) Fixed end moments
These are the same as calculated in the
previous problem:
MFAB =
-2.4 KN-m ; MFBA = +3.6 KN-m
MFBC =
-5.0 KN-m ; MFCB = +5.0 KN-m
(b)
Slope deflection equations.

(c) Equilibrium equations
Since end A is freely supported,
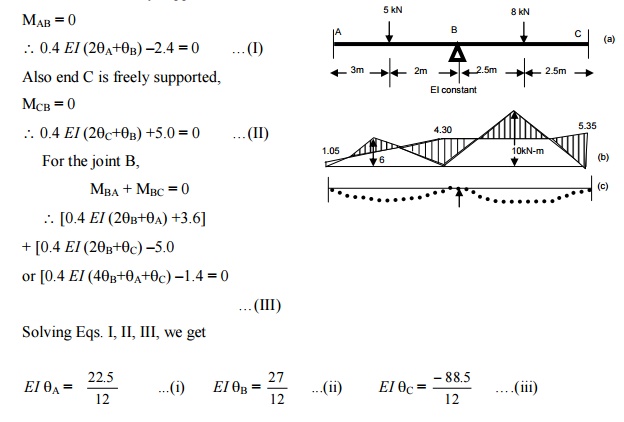
(d) Final moments : Substituting
the values of EI qA
and EI qB
inEq. (2), we get
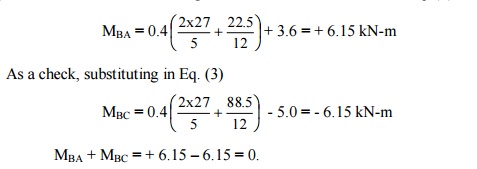
The bending moment diagram and the
deflected shape of the beam are shown in the Fig. Note. The beam is statically
indeterminate to single degree only. This problem has also been solved by the
moment distribution method (example 10.2) treating the moment at B as unknown.
However, in the4 slope- deflection method, the slope or rotations are taken as
unknowns, and due to this the problem involves three unknown rotations qA, qB and qC. hence the method of
slope deflection is not recommended for such a problem.
(3) A continuous
beam ABCD consists of three spans and is loaded as shown in fig. ends A
and D are fixed. Determine the bending moments at the supports and plot the
bending moment diagram.
a)Fixed end moments
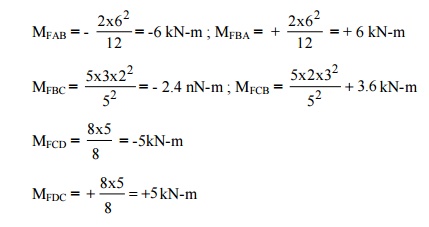
(b) Slope deflection equation
qA
and qD
are zero since ends A and D are fixed.
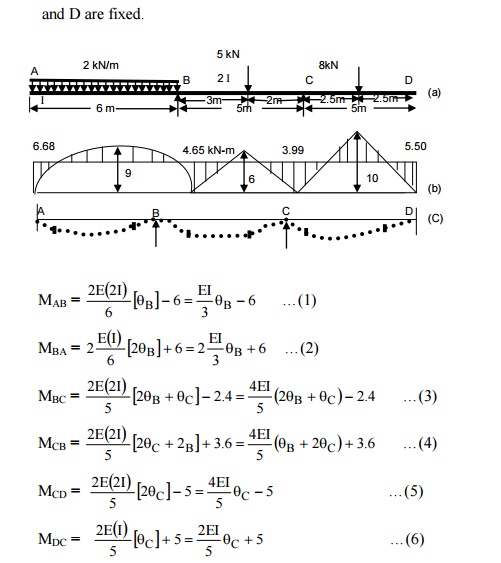
(c)
Equilibrium equations
At join B, MBA + MBC
= 0

At join C, MCB + MCD
= 0
From (I) and (II), we get EI qB
= -2.03 kN-m and EI qC
= + 1.26kN-m
(d)
Final moments
Substituting this values in Eqs. (1) to
(6), we get
The bending moment diagram and the deflected shape
are shown in Figure.
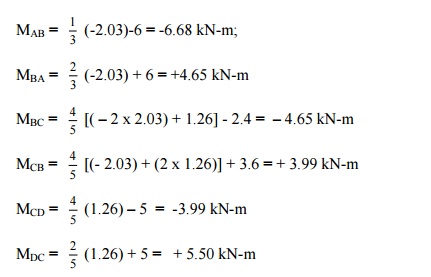
4) A continuous beam
ABC is supported on an elastic column BD and is loaded as shown in
figure . Treating joint B as rigid, analyze the frame and plot the bending
moment diagram and the deflected shape of the structure.
(a)Fixed end moments

MFBD = MFDB = 0
(b)Slope deflection equations.
The slopes qA
and qD
are zero since ends A and D are fixed.
For span AB
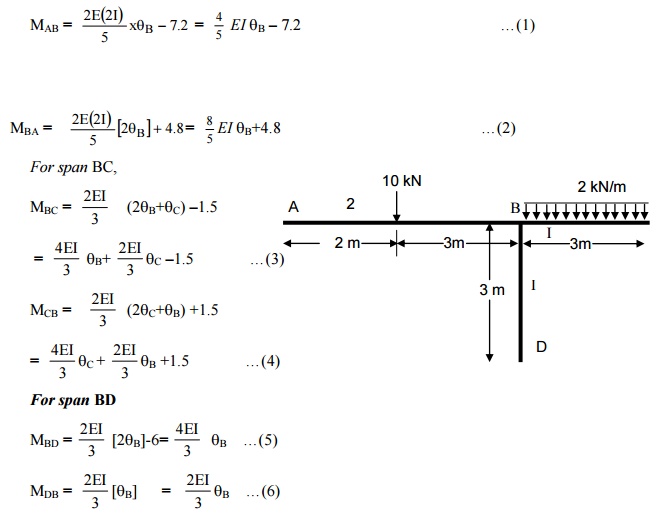
(c) Equilibrium equations
At join B, MBA + MBC
+ MBD = 0
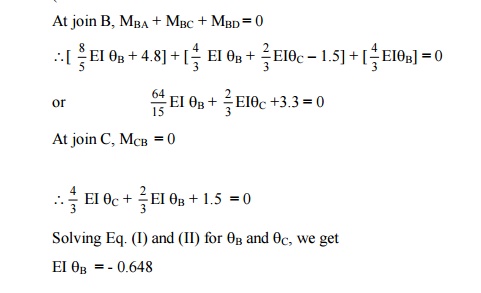
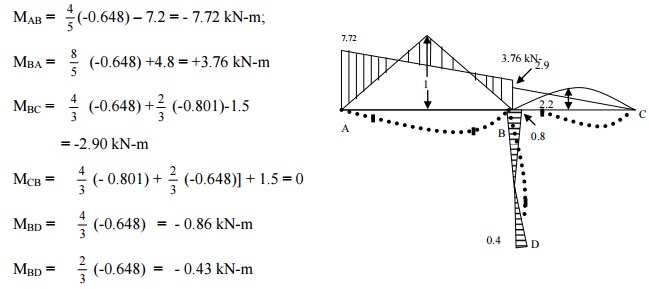
(d) Final moments
Substituting this values in Eqs. (1) to (6), we get
The bending moment diagram and the deflected shape
are shown in Figure.
(5) Analyze the rigid frame shown in
figure
(a) Fixed end moments

(b) Slope deflection equations.

(c)
Equilibrium equations
For the equilibrium
joint B, MBA + MBD
+ MBC = 0
\(2EIqB + 2.67) + (EIqB -2) + (-4) = 0
3EIqB
=
3.33
EIqB
=
1.11
(d)
Final moments
Substituting this value of EIqB in Eqs. (1) to (4), we
get
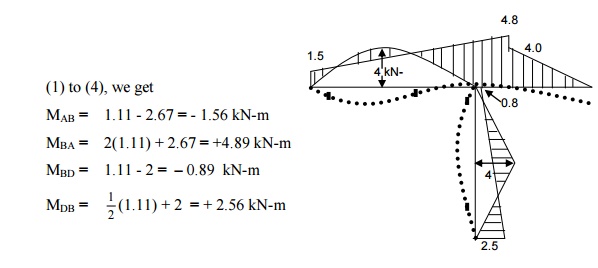
The bending moment diagram and
The deflected shapes are shown in
Figure.
(6) A portal frame
ABCD is fixed at A and D, and has rigid joints at B and C. The column AB
is 3m long. The beam BC is 2m long, and is loaded with uniformly distributed
load of intensity 6 kN/m. The moment of inertia is 2.1 and that of BC and CD is
I (Fig). Plot B.M. diagram and sketch the deflected shape of the frame.
(a)
Fixed end moments
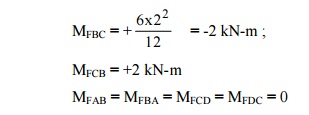
Let the joints B and C move horizontally by d
(b)Slope
deflection equations.
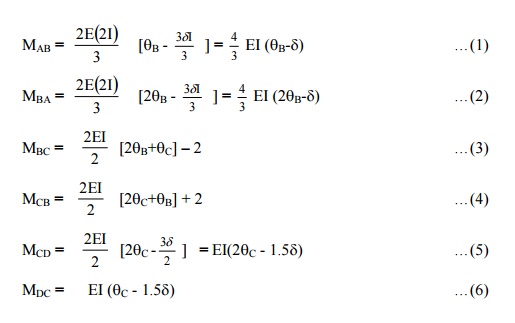
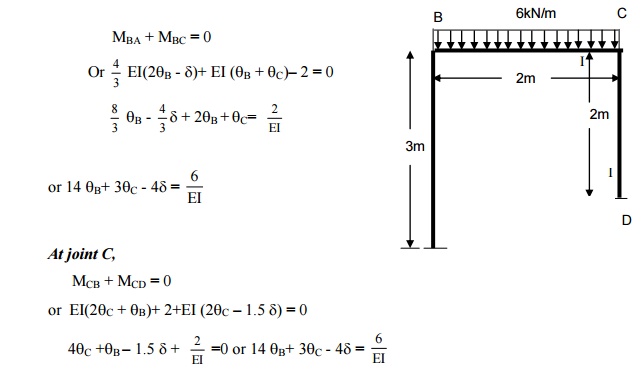
(c) Equilibrium equations.
At joint B,
d )Shear equation


e)
Final moments
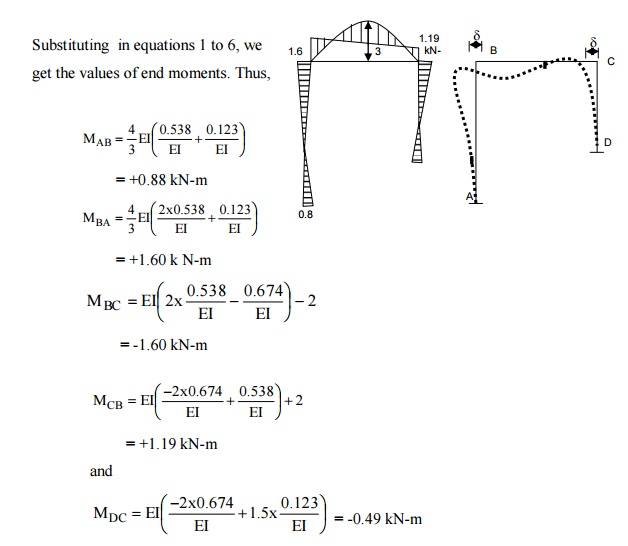
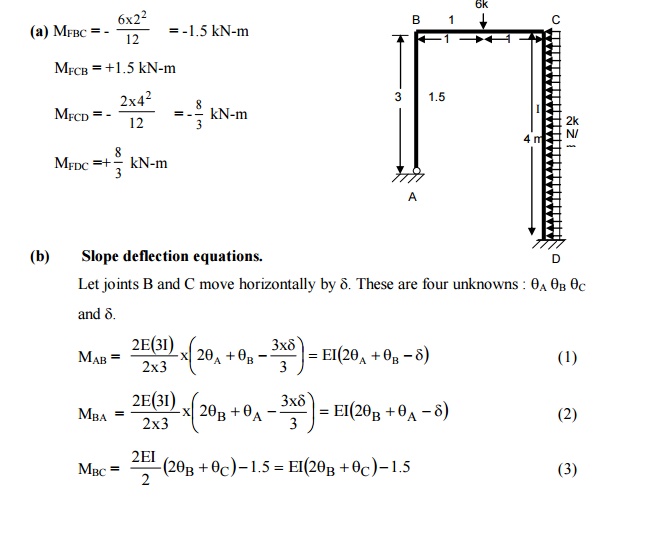
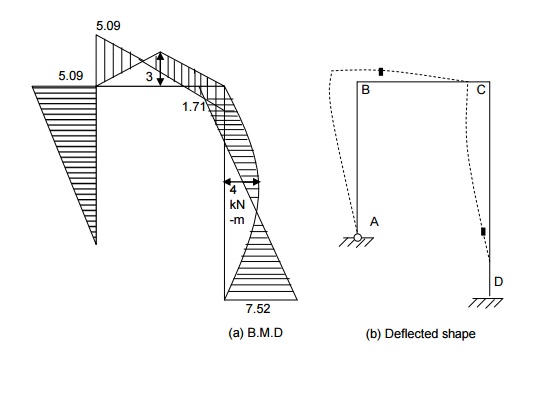
(7) A portal frame
ABCD is hinged at A and fixed at D and has stiff joints at B and C. the
loading is as shown in figure. Draw the bending moment diagram and deflected
shape of the frame.


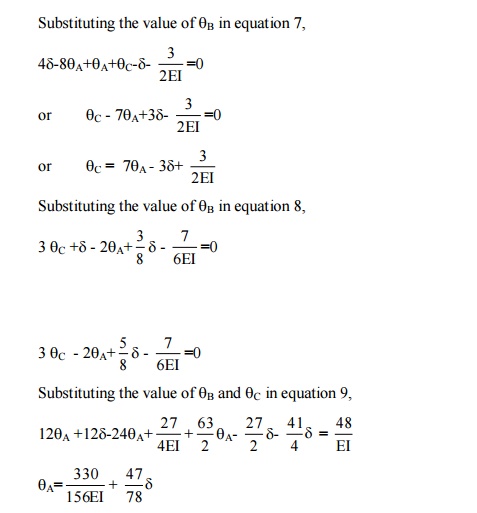

Related Topics