Statistical techniques - Measures of central tendency

Statistical techniques - Measures of central tendency

One of the most important objectives of statistical analysis is to get one single value that describes the characteristics of the entire data. A common word used for measures of central tendency is average. For example, if we collect the  heights of 5000 students of a college, we will have 5000 figures. The persons mind is not capable of registering all the data at a time. So we need a single figure which represents the whole data. This single figure is known as average.

Since an average represents the entire data, its value lies somewhere in between the two extremes i.e. the largest observation and the smallest observation. For this reason the average is frequently referred as measure of central tendency.

Mean

Mean is defined as the value obtained by dividing sum of values of all the given items by the number of items. It is also called as arithmetic mean.

Formula

Mean = Sum of the values of all items / Total number of items

Mathematically it can be shown as

 X=X₁+X₂+X₃+………….X_N / N

X= ∑X/N

X=Menu

∑X = Sum of the Values of all items

N = Total number of items

Example

The following are the monthly average temperature data of Cuddalore District. Find the mean annual temperature

Cuddalore

Solution:

Formula:

=∑X/N

= 25.3+26.58+28.46+30.61+31.32+30.75+30+29.34 +29.03+27.89+26.45+25.36/ 12

= 341.09 12

=28.42

Answer:

The Mean annual temperature of Cuddalore district is 28.42

Calculation of Mean for Grouped Data or Continuous Series

Formula:

 = A + ∑ fd/N × i

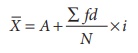
Where

A = Assumed mean

f = frequency

i = class size

d = deviation from assumed mean

N = Total

d = [x – A] / i

Example

Calculate the mean for the following data of heights of the plants in a garden

Solution:

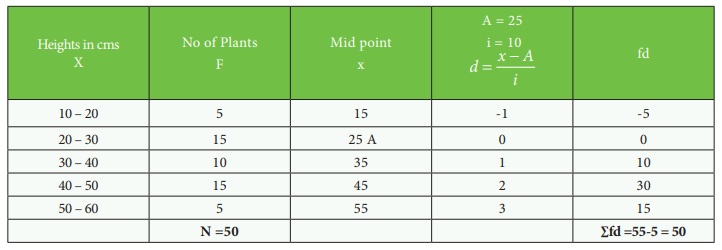
A = 25 , ∑ fd = 50 , N = 50, i = 10

Formula:

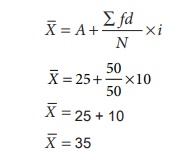
Median:

Median is the middle value of a series arranged in any order – ascending or descending. Median divides the series in to two equal parts.

Calculation of Median

Example

The following are the monthly minimum temperature of Chennai District. Find the median.

Chennai

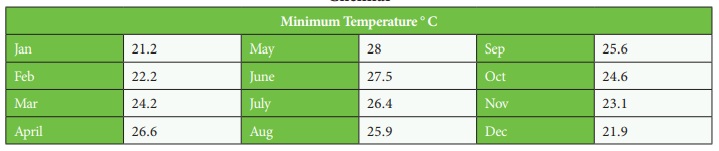
Solution:

Step 1:

Arrange the data in Ascending Order

Step 2:

Formula

M = Value of the ([N+1]/2)^th item

M = Value of the ([12 +1]/2)^th item

M = Value of the (13/2)^th item

M = Value of the 6.5 th item

M = (Size of 6^th  item + size of 7 item)/2

M = (24.6+25.6) / 2.

Answer: M = 25.1 

Calculation of Median for Grouped Data or Continuous Series

Example

Calculate the median for the following data

Literates by age in 2001

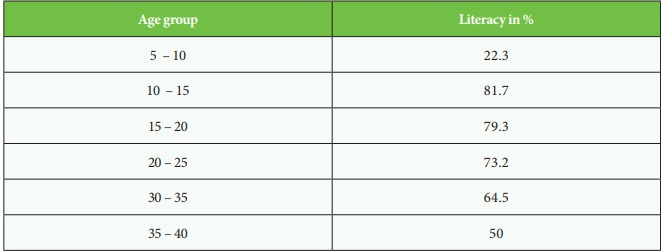
Solution:

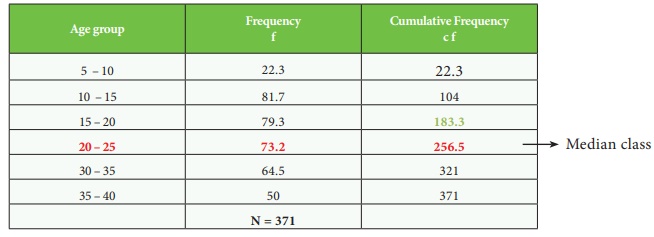
Calculation of Median Class

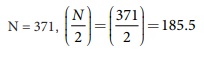
 Class corresponding to 185.5 is 20-25 i.e. the Median Class

Formula

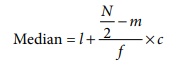
where

I = Lower limit of the median class

N = Total Numbers of frequeny

f = Frequeny of the median class

m = Cumulative frequency of the class preceding the median class

c = The class interval of the median class.

Formula

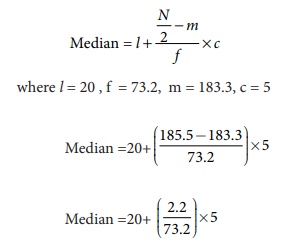
Median = 20 + (0.03 × 5)

Median = 20 + 0.15

Answer: Median = 20.15

Mode

Mode is that value which occurs most frequently in a set of observation or the item which repeats itself the greatest number of times

Calculation of mode

Example

Calculate mode for the following data

Station: Cochin

Solution:

From the data 25 is repeated 3 times. Hence the Mode is 25

Answer: Mode = 25

Calculation of mode for Grouped Data

Example

Calculate the mode for following data

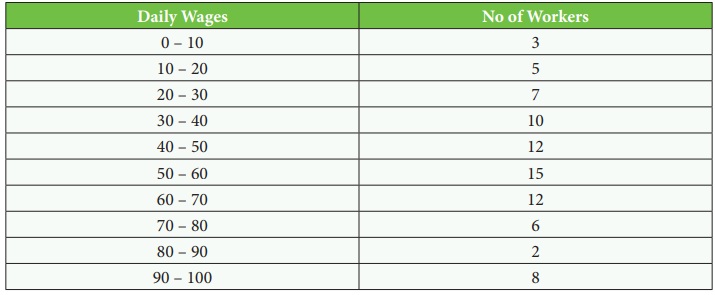
Solution

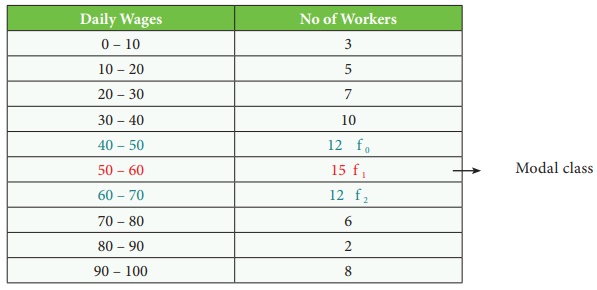
Highest Frequency = 15

Therefore 50 – 60 is the modal class

Formula

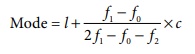
Modal class is the class which has maximum frequency.

f1 = frequency of the modal class

f0 = frequency of the class preceding the modal class

f2 = frequency of the class succeeding the modal class

c= width of the class limits

I = lower limit of mode interval

l = 50, f₀ = 12, f₁ = 15, f₂ = 12

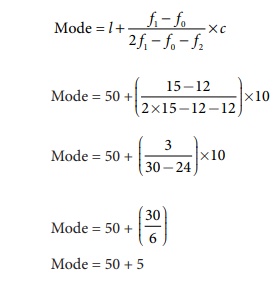
Answer: Mode = 55