Space and Cable Structures

SPACE AND CABLE STRUCTURES

1 ANALYSIS OF SPACE TRUSSES USING METHOD OF TENSION COEFFICIENTS

1.1. Tension Co-efficient Method

The tension co efficient for a member of a frame is defined as the pull or tension in that member is divided by its length.

t = T/l Where t = tension co efficient for the member

T= Pull in the member

l = Length

1.2. Analysis Procedure Using Tension Co-efficient - 2D Frames

1. List the coordinates of each joint (node)of the truss.

2. Determine the projected lengths X_ij and Y_ij of each member of the truss. Determine the support lengths l_ij of each member using the equation l_ij =?X_ij²+Y_ij²

3. Resolve the the applied the forces at the joint in the X and Y directions. Determine the support reactions and their X and Y components.

4. Identify a node with only two unknown member forces and apply the equations of equilibrium. The solution yields the tension co efficient for the members at the node.

5. Select the next joint with only two unknown member forces and apply the equations of equilibrium and apply the tension co efficient.

6. Repeat step 5 till the tension co efficient of all the members are obtained. 7. Compute the member forces from the tension co efficient obtained as above using

Tij= tijx lij

1.3. Analysis Procedure Using Tension Co-efficient - Space Frames

1. In step 2 above the projected lengths Zij in the directions are also computed. Determine the support lengths l_ij of each member using the equation l_ij =?X_ij²+Y_ij² +Z_ij²

2. In step 3 above the components of forces and reactions in the Z directions are also to be determined.

3. In step 4 and 5,each time, nodes with not more than three unknown member forces are to be considered.

Tetrahedron: simplest element of stablespacetruss  ( six members, four joints) expand by adding 3members and1jointeachtime

Determinacy and Stability b+r <3j unstable

b+r=3j statically determinate (check stability)

b+r>3j statically indeterminate (check stability)

Internal Forces

In order to obtain the internal forces at a specified point, we should make section cut perpendicular to the axis of the member at this point. This section cut divides the structure in two parts. The portion of the structure removed from the part in to consideration should be replaced  by the internal forces. The internal forces ensure the equilibrium of the isolated part subjected to the action of external loads and support reactions. A free body diagram of either segment of the  cut member is isolated and the internal loads could be derived by the six equations of equilibrium applied to the segment in to consideration.

5.1. Example

In the following example we shall construct the internal forces diagrams for the given in Fig. space frame structure. The introduced global coordinate system is  shown in the same figure.

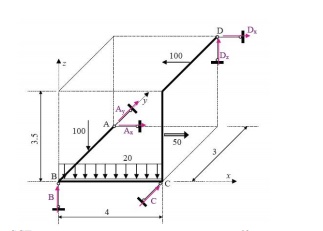
The introduced local coordinate systems of the different elements of the space frame are presented in Fig. The typical  sections where the internal forces must be calculated, in order to construct the relevant diagrams, are numbered from 1 to 8 in the same figure. The typical  sections are placed atleast at the beginning and at the end of each element (segment) of the frame. The internal forces diagrams, in the limits of each element, could be derived by using the corresponding reference and base diagrams.

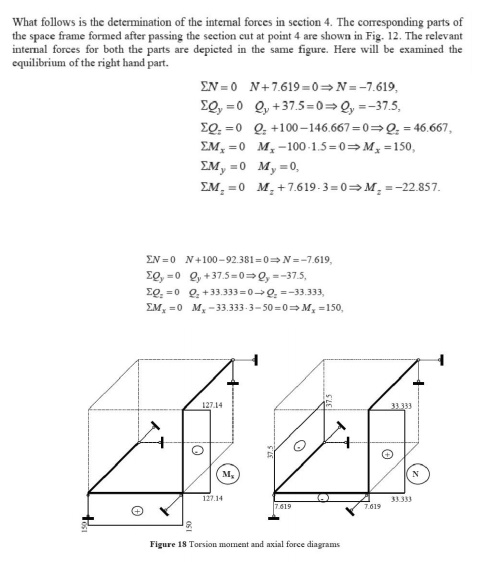
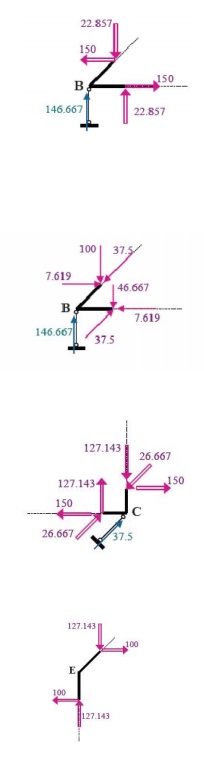
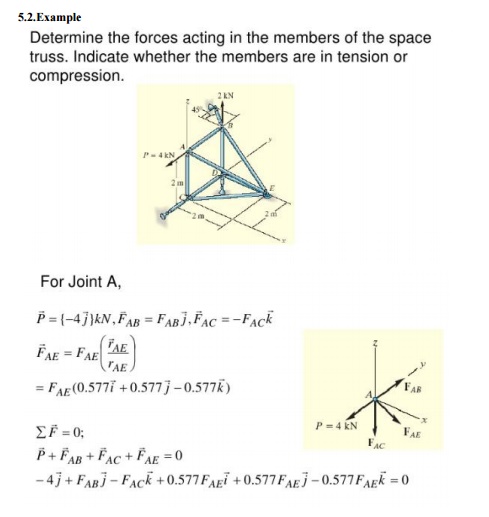
2 BEAMS CURVED IN PLAN

2.1Introduction

Arches are in fact beams with an initial curvature. The curvature is visible only in elevation. In plan they they would appear in straight. the other cases of curved beams are ring beams supporting water tanks, Silos etc., beams supporting corner lintels and curved balconies etc., Ramps in traffic interchanges invariably have curved in plan beams.

Curved beams in addition to the bending moments and shears would also develop torsional moments.

2.2. Moment, Shear and Torsion

The three diverse force components have one thing in common - the strain energy stored in a beam due to each type of force. Among the 3 we normally ignore the strain energy due to shear forces as negligible.

U = ?M²ds/2EI+?T²ds/2GJ

3. SUSPENSION CABLE

3.1. Indroduction

Cables and archesareclosely related to each other and hence they are grouped in this course in the same module. For long span structures (fore.g.in case bridges) engineers commonly use cable or arch construction due to their efficiency. In the few previous pages, cables subjected to  uniform and concentrated loads are discussed. In the few previous pages, arches in general and threehingedarchesin particular along with illustrative examples are explained.

In the last few pages, two hinged arch and hinge less arches are considered. Structure may be classified into rigid and deformable structures depending on change in geometry of the structure while supporting the load. Rigid structures support externally applied loads without appreciable change in their shape (geometry). Beams trusses and frames are examples of rigid structures.

Unlike rigid structures, deformable structures undergo changes in their shape according to externally applied loads. However, it should be noted that deformations are stillsma ll. Cables and fabric structures are deformable structures. Cables are mainly used to support suspension roofs, bridges and cable car system. They are also used in electrical transmission lines and for structure supporting radio antennas. In the following sections, cables subjected to concentrated load and cables subjected to uniform loads are considered.

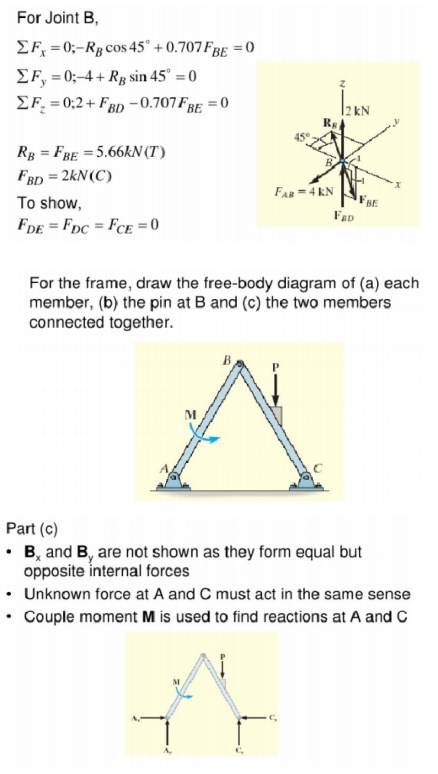
The shape assumed by aropeorachain (with no stiffness) under the action of external loads when hung from two supports is known as a funicular shape. Cable is a funicular structure. It is easy to visualize that a cable hung from two supports subjected to external load must be intens cable. A cable may be defined as the structure inpure tension having the funicular shape of the load. (vide Fig.5.1and 5.2).

As stated earlier, the cables are considered to be perfectly flexible (no flexural stiffness) and in extensible. As they are flexible they donot resistshear force and bending moment. It is subjected to axial tension only and it is always acting tangential to the cable at any point along the length. If the weight of the cable is negligible as compared with the externally applied loads then its self weight is neglected in the analysis. In the present analysis self weight is not considered.

Consider a cable as loaded in Fig.5.3. Let us assume that the cable lengths and sagat() are known. The four reaction component sat ACDEB and B, cable tensions in each of the four segments and three sag values: a total of eleven unknown quantities are to be determined. From the geometry, one could write two force equilibrium equations (0,0==??yxFF) at each of the point and DCBA,,,Ei.e. a total of ten equations and the required one more equation may be written from the geometry of the cable. For example, if one of the sag is given then the problem can be solved easily. Otherwise if the total length of the cable is given then the required equation may be written as

Fig 5.3Cable in Tension                   

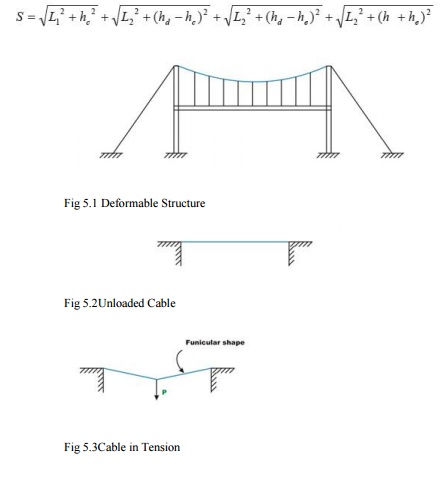
Cable subjected to uniform load.                         

Cables are used to support the dead weight and live loads of the bridge decks having long spans.

The bridge decks are suspended from the cable using the hangers. The stiffened deck prevents the supporting cable from       changing its shape by distributing the live load moving over it, for a longer length of cable. In          such cases   cable is assumed to be uniformly loaded.

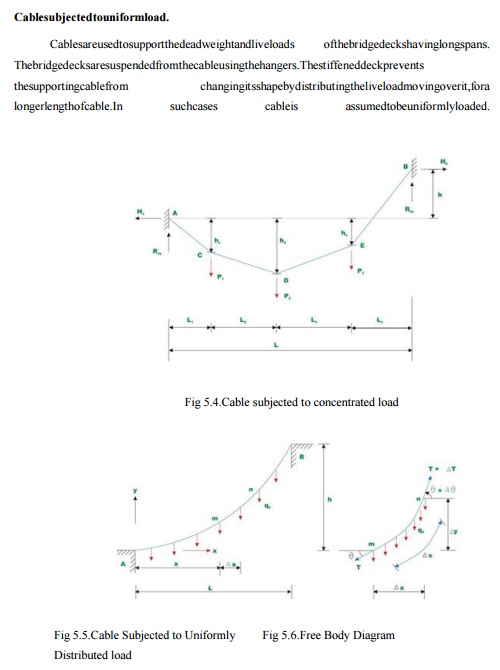
Consider a cable which is uniformly loaded as shown in Fig 5.4.

Due to uniformly distributed load, the cable takes a parabolic shape. However due to its own dead weight it takes a shape of acatenary. However dead weight of the cable is neglected in the present analysis.

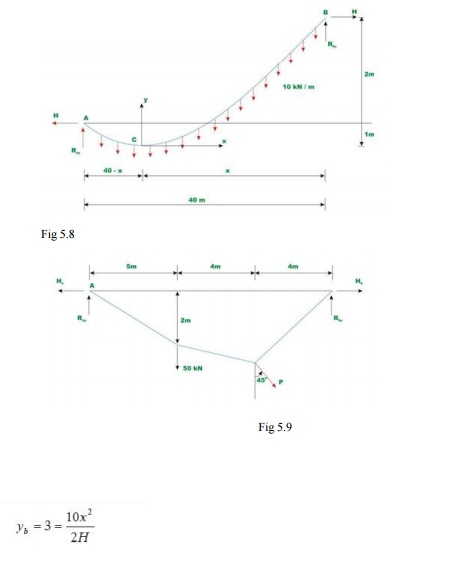
5.3. Example

Determine reaction components at A and B, tension in the cable and the sag of the cable shown inFig.5.7. Neglect the self weight of the cable in the analysis.

Since there are no horizontal loads, horizontal reactions at A and B should be the same. Taking moment about E, yields

CABLE AND SPACE STRUCTURES

1. What are cable structures?

Long span structures subjected to tension and uses suspension cables for supports. Examples of cable structures are suspension bridges, cable stayed roof.

Suspension bridge- cable structure

2. What is the true shape of cable structures?

Cable structures especially the cable of a suspension bridge is in the form of a catenary. Catenary is the shape assumed by astring/cable freely suspended between two points.

3. What is the nature of force in the cables?

Cables of cable structures have only tension and no compression or bending.

4. What is a catenary?

Catenary is the shape taken up by a cable or rope freely suspended between two supports and under its own self weight.

5. Mention the different types of cable structures.

Cable structures are mainly of two types: (a) Cable over a guide pulley (b)Cable over a saddle

6. Briefly explain cable over a guide pulley.

Cable over a guide pulley has the following properties:

·       Tension in the suspension cable=Tension in the anchor cable

·       The supporting tower will be subjected to vertical pressure and bending due to net horizontal cable tension.

7. Briefly explain cable over saddle.

Cable over saddle has the following properties:

·        Horizontal component of tension in the suspension cable=Horizontal component of tension in the anchor cable

·        The supporting tower will be subjected to only vertical pressure due to cable tension.

8. What is the degree of indeterminacy of a suspension bridge with two hinged

stiffening girder?

The two hinged stiffening girder has one degree of indeterminacy.

9. What are the main functions of stiffening girders in suspension bridges?

Stiffening girders have the following functions.

·They help in keeping the cables in shape

·They resist part of shear force and bending moment due to live loads.

10.            Differentiate between planetruss and spacetruss.

Planetruss

·       All members liein one plane

·       All joints are assumed to be hinged.

Spacetruss

·       This is a three dimensional truss

·       All joints are assumed to be ball and socketed.

11.            Define tension coefficient of a truss member.

The tension coefficient for a member of a truss is defined as the pull or tension in the member divided by its length, i. e. the force in the member per unit length.

12.            Give some examples of beams curved in plan.

Curved beams are found in the following structures.

Beams in a bridge negotiating a curve

·       Ring beams supporting a water tank

·       Beams supporting cornerlintels

·       Beams in ramps

13.            What are the forces developed in beams curved in plan?

Beams curved in plan will have the following forces developed in them:

·       Bending moments

·       Shear forces

·       Torsional moments

14.            What are the significant features of circular beams on equally spaced supports?

·       Slope on either side of any support will be zero.

·       Torsional moment on every support will be zero

15.            Give the expression for calculating equivalent UDL on a girder.

Equivalent UDL on a girder is given by We:

16.            Give the range of central  dip of a cable.

The central dip of acablera nges from 1/10 to 1/12 of the span.

17.            Give the horizontal and vertical components of a cable structure subjected to UDL.

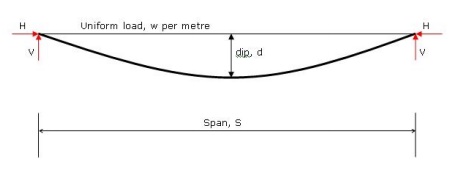
18. Give the expression for determining the tension T in the cable.

The tension developed in the cable is given by 

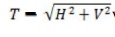
Where H=horizontal component and V=vertical component.

19.            Give the types of significant cable structures

Linear structures

·       Suspension bridge s

·       Draped cables

·       Cable-stayed beams or trusses

·       Cable trusses

·       Straight tensioned cables

Three-dimensional structures

·       Bicycle wheel roof

·       3D cable trusses

·       Tensegrity structures

·       Tensairity structures

20.            What are cables made of?

Cables can be of mild steel, high strength steel, stainless steel, or polyest er fibres. Structural cables are made of a series of small strandstwistedor bound together to form a much larger cable. Steel cables are either spiral strand, where circular rodsaretwisted together or locked coil strand, where individual interlocking steel strands form the cable (often with aspiral strand core).

Spiral strand is slightly weaker than locked coil strand. Steel spiral strand cables have a Young's modulus, Eof150 ± 10kN/mm² and come in sizes from 3 to 90 mm diameter. Spiral strand suffers from construction stretch, where the strands compact when the cable is loaded.