Suspension Cable Structural Analysis

SUSPENSION CABLE

1. Indroduction

Cables and archesareclosely related to each other and hence they are grouped in this course in the same module. For long span structures (fore.g.in case bridges) engineers commonly use cable or arch construction due to their efficiency. In the few previous pages, cables subjected to  uniform and concentrated loads are discussed. In the few previous pages, arches in general and threehingedarchesin particular along with illustrative examples are explained.

In the last few pages, two hinged arch and hinge less arches are considered. Structure may be classified into rigid and deformable structures depending on change in geometry of the structure while supporting the load. Rigid structures support externally applied loads without appreciable change in their shape (geometry). Beams trusses and frames are examples of rigid structures.

Unlike rigid structures, deformable structures undergo changes in their shape according to externally applied loads. However, it should be noted that deformations are stillsma ll. Cables and fabric structures are deformable structures. Cables are mainly used to support suspension roofs, bridges and cable car system. They are also used in electrical transmission lines and for structure supporting radio antennas. In the following sections, cables subjected to concentrated load and cables subjected to uniform loads are considered.

The shape assumed by aropeorachain (with no stiffness) under the action of external loads when hung from two supports is known as a funicular shape. Cable is a funicular structure. It is easy to visualize that a cable hung from two supports subjected to external load must be intens cable. A cable may be defined as the structure inpure tension having the funicular shape of the load. (vide Fig.5.1and 5.2).

As stated earlier, the cables are considered to be perfectly flexible (no flexural stiffness) and in extensible. As they are flexible they donot resistshear force and bending moment. It is subjected to axial tension only and it is always acting tangential to the cable at any point along the length. If the weight of the cable is negligible as compared with the externally applied loads then its self weight is neglected in the analysis. In the present analysis self weight is not considered.

Consider a cable as loaded in Fig.5.3. Let us assume that the cable lengths and sagat() are known. The four reaction component sat ACDEB and B, cable tensions in each of the four segments and three sag values: a total of eleven unknown quantities are to be determined. From the geometry, one could write two force equilibrium equations (0,0==??yxFF) at each of the point and DCBA,,,Ei.e. a total of ten equations and the required one more equation may be written from the geometry of the cable. For example, if one of the sag is given then the problem can be solved easily. Otherwise if the total length of the cable is given then the required equation may be written as

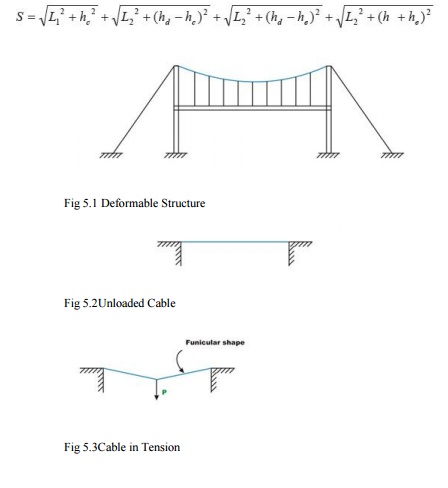
Fig 5.3Cable in Tension                   

Cable subjected to uniform load.                         

Cables are used to support the dead weight and live loads of the bridge decks having long spans.

The bridge decks are suspended from the cable using the hangers. The stiffened deck prevents the supporting cable from       changing its shape by distributing the live load moving over it, for a longer length of cable. In          such cases   cable is assumed to be uniformly loaded.

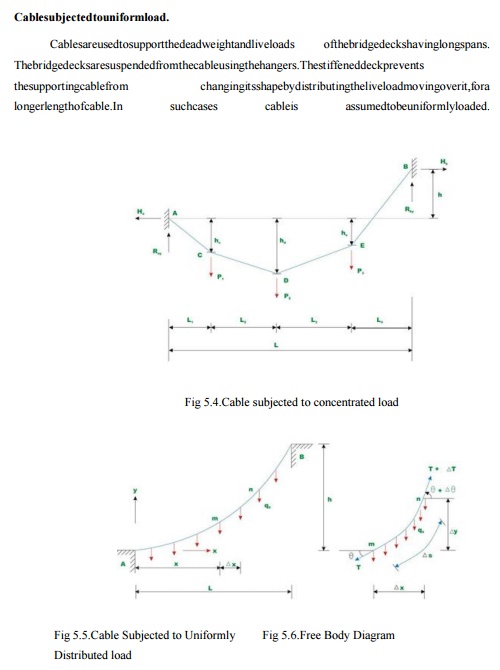
Consider a cable which is uniformly loaded as shown in Fig 5.4.

Due to uniformly distributed load, the cable takes a parabolic shape. However due to its own dead weight it takes a shape of acatenary. However dead weight of the cable is neglected in the present analysis.

Example

Determine reaction components at A and B, tension in the cable and the sag of the cable shown inFig.5.7. Neglect the self weight of the cable in the analysis.

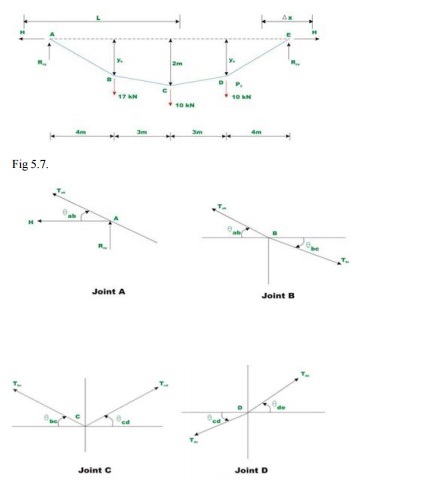
Since there are no horizontal loads, horizontal reactions at A and B should be the same. Taking moment about E, yields