Solved Problems: Optics

Optics Science

SOLVED PROBLEMS

Problem 1

Light rays travel from vacuum into a glass whose refractive index is 1.5. If the angle of incidence is 30°, calculate the angle of refraction inside the glass.

Solution:

accorting to Snell’s law,

sin i / sin r = µ2/ µ1

µ1 sin i = µ2 sin r

Here µ1 = 1.0,

µ2 = 1.5, i = 30°

(1.0) sin 30° = 1.5 sin r

1× 1/2 = 1.5 sin r

sin r = 1/(2×1.5) = 1/3 = (0.333)

r= sin–1 (0.333)

r = 19.45°

Problem-2

A beam of light passing through a diverging lens of focal length 0.3m appear to be focused at a distance 0.2m behind the lens. Find the position of the object.

Solution:

f = −0.3 m, v = −0.2 m

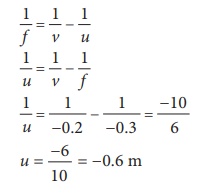
Problem-3

A person with myopia can see objects placed at a distance of 4m. If he wants to see objects at a distance of 20m, what should be the focal length and power of the concave lens he must wear?

Solution:

Given that x = 4m and y = 20m.

Focal length of the correction lens is

f =    xy /  x−y  (Refer eqn.2.7)

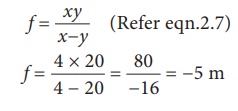
Power of the correction lens

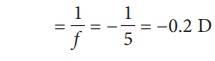
Problem-4

For a person with hypermeteropia, the near point has moved to 1.5m. Calculate the focal length of the correction lens in order to make his eyes normal.

Solution:

Given that, d = 1.5m; D = 25cm = 0.25m (For a normal eye).

From equation (2.8), the focal length of the correction lens is

f =  d × D /  d − D =  1.5 × 0.25 / 1.5 − 0.25 =  0.375 / 1.25 = 0.3 m