Solved Problems: Heat and Mass Transfer - Mass Transfer

1. A vessel contains a mixture of2 kmol of CO2 and 4.5 kmol of air at 1 bar and 25°C.ifair contains 21 % oxygen and 79% nitrogen by volume, calculate for themixture:

(i) The mass of CO₂, O₂ and N₂, and the total mass;

(ii) The percentage carbon content by mass;

(iii) The molar mass and the gas constant for the mixture;

(iv)The specific volume of the mixture.

Solution: (1) Number of moles of O₂ = 0.21 × 4.5 = 0.945 kmol, Number of moles of N₂ = 0.79 × 4.5 = 3.55 kmol

Mass of CO₂ = 2 × 44 = 88kg; Mass of O₂ = 0.945 × 32 = 30.24 kg Mass of N₂ = 3.55 × 28 = 99.54 kg

The total mass = 88 + 30.24 + 99.54 = 217.48 kg

(ii) Percentage of carbon in the mixture; (24/217.48) × 100 = 11.035% by mass.

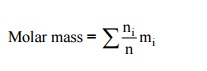
= (2/6.5) × 44 + (0.945; 6.5) × 32 + (3.555/6.5) × 28

= 33.5 kg/kmol

And the gas constant of the mixture; 8314/33.5 = 248.18 J/kgK (iv)Specific volume of the mixture, v = RT/p = 248.18 × 298/ (l × 10⁵) = 0.7395 m³/kg.

2. The air pressure inside a synthetic rubber ball (400 mm inside diameter and 15 thick decreases from 3.5bar to 3.45bar in seven days. Estimate the coefficient of diffusion of air in synthetic rubber if the temperature is 25°C and the solubility of air in the rubber is 1.8 ×

10^-3 kmol/m³ bar.

Solution: Since the pressure change is very small during a period of seven days, the problem can be treated as quasi-steady. The initial mass of air inside the ball

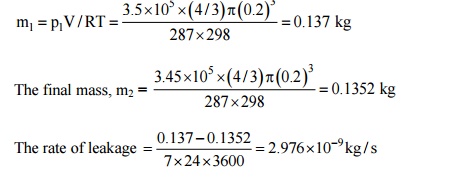
The average pressure inside the ball = (3.45 + 3.5)/2 = 3.475 bar

Concentration inside the ball = = 0.1814 kg/m³

3.Estimate the rate of burning of a pulverized carbon particle in a furnace if the diameter of the particle is 4 mm, pressure 1 bar. The oxygen is available at 1100 K. Assume that fairly large layer of CO₂ surrounds the carbon particle. Take D = 1 cm²/s.

Solution: The combustion equation is C + O₂® CO₂, i.e., there will be an Equimolal counter-diffusion between O₂ and CO₂,

Since a fairly large blanket of carbon dioxide surrounds the carbon particle, the partial pressure of carbon dioxide at the surface of the carbon particle will be 1 bar and the partial pressure of oxygen will be zero. Similarly, the partial pressure of carbon dioxide far outside will be zero and the partial pressure of oxygen will be 1 bar.

4. Carbon dioxide at 30°C and at a pressure of 2.5bar is flowing through a rubber pipe, inside diameter 25 mm and thickness 5 mm. The coefficient of diffusion of carbon dioxide-rubber combination is 0.11 × 10^-9 m²/s and the solubility of carbondioxide 4 × 10^-2 k mol/m³ bar. Calculate the loss of CO₂ by diffusion per unit length of the pipe.

Solution: The species concentration at the gas-solid interface is obtained in terms of the partial pressure of the gas adjacent to the solid surface and a solubility factor, S.

Or, Concentration = Partial pressure × S

The carbon dioxide is flowing through the rubber tube at 2.5bar. As such, the partial pressure of CO, at the rubber-gas interface is 2.5bar and the concentration is then,

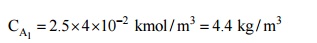
Assuming that at the outer surface of the rubber pipe, the partial pressure of carbon dioxide is zero, the concentration at the outer surface is zero. Further, the diffusion mass transfer is analogous to conduction heat transfer, the diffusion resistance in cylindrical system can be written as,

R_D =ln (r₂ / r₁ )/(2 pLD)

=ln (17.5 /12.5 )/(2 ´3.142  1´0.´11  10^-´⁹)= 4.867 × 10⁸

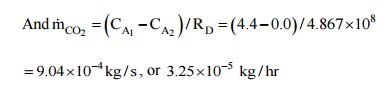
5.       The air pressure inside a synthetic rubber ball (400 mm inside diameter and 15 mm thick) decreases from 3.5bar to 3.45bar in seven days. Estimate the coefficient of diffusion of air in synthetic rubber if the temperature is 25°C and the solubility of air in the rubber is 1.8 × 10^-3 kmol/m³ bar. (AU2011)

Solution: Since the pressure change is very small during a period of seven days, the problem can be treated as quasi-steady. The initial mass of air inside the ball