Mass Transfer

MASS TRANSFER

BASIC CONCEPTS

Air is a mixture of various gases. Whenever we have a multicomponent system with a concentration gradient, one constituent of the mixture gets transported from the region of higher concentration to the region of lower concentration till the concentration gradient reduces to zero. This phenomenon of the transport of mass as a result of concentration gradient is called 'Mass Transfer'.

The mass transfer phenomenon is analogous to heat transfer phenomenon. In heat transfer - heat energy flows in a direction of decreasing temperature gradient and ceases when the temperature gradient reduces to zero. In mass transfer - the transfer of mass takes place in the direction of decreasing concentration gradient and ceases when the concentration gradient is zero.

The. common examples of mass transfer in our everyday life and in many

industries are:

-  diffusion of smoke discharged by tall chimney into the atmosphere,

-  a drop of ink diffusing in a glass of still water,

-  evaporation of a drop of perfume in a room,

-  humidification of air flowing over a spray pond or cooling tower,

-  mixing of diesel or petrol with air inside an internal combustion engine,

-  diffusion welding of metals,

-  diffusion of neutron in a nuclear reactor.

Different Modes of Mass Transfer

There are basically two modes of mass transfer:

(i)  Mass Transfer by Diffusion - the transport of mass by random molecular motion in quiescent or laminar flowing fluids is known as mass transfer by 'diffusion' and is analogous to heat transfer by conduction. Mass transfer by diffusion occurs due to (a) concentration gradient,

(b) temperature gradient, and (c) hydrostatic pressure difference.

(ii)    Convective Mass Transfer - the rate of molecular diffusion of mass can be accelerated by the bulk motion of the fluid. Mass can be transported between the boundary of a surface and a moving fluid (drying of clothes, molecular diffusion of a sugar cube in a cup of coffee by stirring, moist air flowing over the surface of an ocean and precipitation on a dry land etc.), or between two moving fluids which are relatively immiscible (formation of clouds, vapourisation of water in a tea kettle). This mechanism of mass transfer is called 'convectIve mass transfer' and is analogous to heat transfer by convection (free or forced).

Dalton's Law of Partial Pressure

Each constituent of a multicomponent system contributes to the total pressure by an amount which is known as the 'partial pressure' of the constituent. The relationship between the partial pressures of the constituents is expressed by Dalton's Law:

The pressure of a mixture of gases is equal to the sum of the partial pressure of the constituents. The partial pressure of each constituent is that pressure which the gas would exert if it occupied alone that volume occupied by the mixture at the same temperature.

For a mixture of ideal gases, we have

P = P_A + P_B + ...... + P_K;

where P_A is the partial pressure of the species A and so on.

=  P_D                       ……….(5.1)

Dalton's law was reformulated by Gibbs to include a second statement on the properties of mixtures. The combined statement is Gibbs-Dalton law:

The internal energy. enthalpy and entropy of a gaseous mixture are respectively equal to the sum of the internal energies, enthalpies, and entropies of the constituents. The internal energy, enthalpy and entropy which a constituent would have if it occupied alone that volume occupied by the mixture at the temperature of the mixture.

Molar Density, Mass Density, Mass Fraction and Mole Fraction

There are a number of ways by which the concentration for a species in a multicomponent mixture can be defined:

(i) Molar Density or Molar Concentration, C_A = number of moles of the species A per unit volume of mixture, kg-mol/m³

A = mass of the species A per unit volume of the mixture, kg/m³.

(iii) Mass Fraction, m_A = mass concentration of component A / total mass density of the

mixture.

(iv) Mole Fraction, X_A = number of moles of species A / total number of moles of the mixture. = C_A/C

Therefore, the following summation rules hold true:

C_A + C_B + .... + C_K = C

CA + CB + .... + CK = C

X_A + X_B + ..... + X_K = I1

rn_A + m_B + ..... + m_K  = I                    (5.2)

Since the number of moles = mass of species/molecular weight, we have

C _AA  = r/ M_A

For a perfect gas, we have:

P_A V =n _A R _oT , where Ro is the universal gas constant,

and,  C_A =n _A / V  =P_A / R _oT

X _A =C_A / C  =P_A / P and C =p / R _oT

 Mass Average and Molar Average Velocities and Different Types of Fluxes Velocity

In a multicomponent mixture, the bulk velocity of the mixture can be defined on the basis of mass average or molar average velocity. Let VA       A is the mass density of the species A, then the mass average velocity would be:

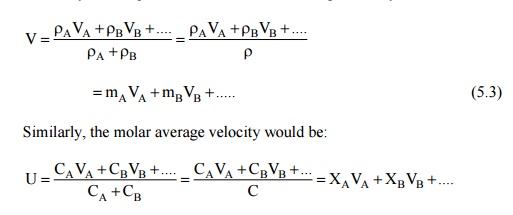
Since mass transfer requires the diffusion of a species with respect to a plane moving with an average velocity, diffusion will take place when the diffusion velocity is in excess of the average velocity. Thus

        Mass diffusion velocity of the species A : VA –V         (5.4)

        Molar diffusion velocity of the species A : VA - U        (5.5)

Fluxes: The mass flux of species A can be expressed relative to either a fixed observer or an observer moving with the bulk velocity. For a stationary observer, the absolute flux of any species A will be equal to the sum of the flux due to the molecular diffusion and that due to the bulk motion.

Similarly, molar diffusion flux = C_A(V_A –V)

Fick's Law of Diffusion

The fundamental equation (one-dimensional) of molecular diffusion is known as Fick's law. It has been derived from the kinetic theory of gases, and can be written for a binary mixture as

J_A = –D_AB (d C_A/dx)                                                            (5.8)

where  D_AB   =  diffusion  coefficient  of  species  A  with  respect  to  species  B,

J_A = molar flux in the X-direction relative to the molar average velocity,

dC_A/dx = Concentration gradient in X-direction.

Let us consider a two compartment tank as shown in Fig. 5.1. One compartment contains gas A and the other compartment contains gas B and both the compartments are initially at a uniform pressure and temperature throughout. When the partition between the compartments is removed, the two gases will diffuse through each other until equilibrium is established and the concentration of the gases is uniform throughout the tank.

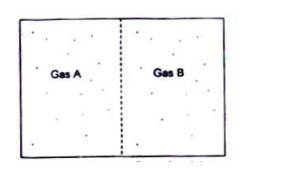
Fig. 5.1 Diffusion of species A in to species B

Fig 5.2 illustrates the dependence of diffusion on the concentration profile. The concentration of the species A on the left side of the imaginary plane is greater than that on the right side. As such, more molecules will cross the plane per unit time from left to right. This would lead to a net transfer of mass from the region of higher concentration to the region of lower concentration.

Fig. 5.2 Dependence of diffusion on concentration profile

* This law assumes that fluxes are measured relative to the coordinates that move with the average velocity of the mixture.

CONVECTIVE MASS TRANSFER :

(i) Diffusion in Gases - the diffusion rates in gases are dependent on the molecular speed which is a function of temperature and therefore, the diffusion coefficient depends upon the temperature of gases.

Gilliland has proposed a semi-empirical equation for diffusion coefficient in a binary gas mixture –

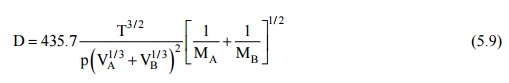
where D is in square centimeters per second, T is in Kelvin, p is the total pressure of the system in pascals, V_A and V_B are the molecular volumes of the species A and R as calculated from the atomic volumes in Table 12.1, M_A and M_B are the molecular weights of species A and B.

Diffusion coefficients for gases depend upon pressure, temperature and other molecular properties of diffusing gases. At two different pressure and temperature, we have

Table 5.1 Atomic volumes*

Air   29.9   In secondary amines      1.2

Bromine    27.0   Oxygen, molecule (O2)  7.4

Carbon      14.8   Coupled to two other elements:       

Carbon dioxide   34.0   In aldehydes and ketones        7.4

Chlorine             In methyl esters    9.1

Terminal as in R-Cl      21.6   In ethyl esters       9.9

Medial as in R-CHCl-R         24.6   In higher esters & ethers          11.0

Flourine    8.7     In acids       12.0

Hydrogen, molecule (H2)       14.3   In union with S, P, N     8.3

in compounds     3.7     Phosphorous        27.0

Iodine        37.0   Sulphur      25.6

Nitrogen, molecule (N2)        15.6   Water          18.8

in primary amines        10.5           

*(For three numbered ring like ethylene oxide, deduct 6.0, for four numbered ring like cyclobutane, deduct 8.5, for six numbered ring like benzene, deduct 15.6, for napthelene ring, deduct 30.0.)

(ii) Diffusion in Liquids and Solids - Diffusion in liquids occurs at much slower rate than in gases. Since kinetic theory of liquids is not as much developed as that of gases, it is usually assumed as a first approximation that equations of the same general form are applicable to the diffusion of a solute in a solvel1t as to the diffusion in gases, i.e., Fick's law is assumed valid for liquids.

Diffusion coefficient for most of the common organic and inorganic materials in the

usual solvents such as water, alcohol and benzene at room temperature lie m the range of 1.79 × 10^-3 to 1.075 × 10^-7 cm²/s.

Diffusion in solids is much slower than in liquids. Diffusion of solids in solid has limited engineering applications but diffusion of fluids in solids have extensive applications. Fick's law is sometimes used, with an empirically determined effective diffusivity which takes care of the structure of solid. A typical problem of liquid transfer in a solid, of interest, is drying of solids.

HEAT AND MASS TRANSFER ANALOGY:

Fick's law (Eq. 5.8) can also be expressed in terms of mass flux per unit area or mass concentration or in terms of molal concentrations and fluxes. For gases, the law may be expressed in terms of partial pressures by making use of the perfect gas equation of state:

Since the characteristic gas constant of a gas is: R_A = R_o/M_A

When we have equimolal counter diffusion, shown in Fig. 12.3 (a, b), the steady state molal diffusion rates of the species A and B, represented by N_A and N_B will be given by

The total pressure of the system remains constant at steady state,

or, p = p_A + p_B ;  and dp_A/dx + dp_B/dx = 0

as  dp_A/dx = –dp_B/dx

Since each molecule of A is replaced by a molecule of B, the molal diffusion rates must be equal. Thus: N_A = –N_B, and

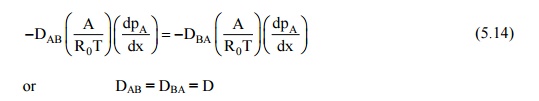
Or D_AB = D_BA = D

This fact is known as the equivalence of diffusion coefficients or diffusivities in binary mixtures, and is a property of the binary mixture.

By integrating Eq. (12.10), we can obtain the mass flux of the species A as;

corresponding to the nomenclature used in Fig. 5.3 (a, b). Table 5.2 gives the values of the binary diffusion coefficients.

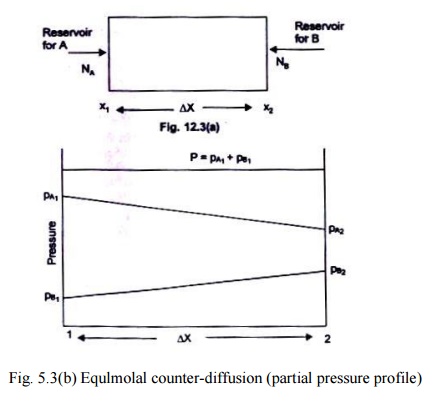
Fig. 5.3(b) Equlmolal counter-diffusion (partial pressure profile)

(iv) It does not tell about diffusion due to temperature or pressure gradient or due to external forces.

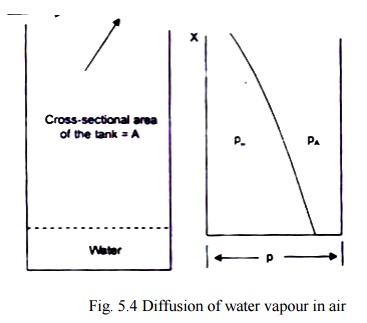
CONVECTIVE MASS TRANSFER CORRELATIONS :

Let us consider a tank containing water which is exposed to air in the tank as shown in Fig. 5.4. We assume that:

(i) the system is isothermal,

(ii) the total pressure remains constant,

(iii) the system is in steady state. Since there has to be a little movement of air over the top of the tank to remove the water vapour that diffuses to that point, the air movement does not create any turbulence to alter the concentration profile in the tank, and

air and water vapour both behave like ideal gases.

From Eq. (5.10), the downward diffusion of air can be written as

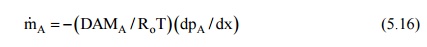
and this has to be balanced by the bulk mass transfer upward. Therefore,