Dalton's Law of Partial Pressure

Dalton's Law of Partial Pressure

Each constituent of a multicomponent system contributes to the total pressure by an amount which is known as the 'partial pressure' of the constituent. The relationship between the partial pressures of the constituents is expressed by Dalton's Law:

The pressure of a mixture of gases is equal to the sum of the partial pressure of the constituents. The partial pressure of each constituent is that pressure which the gas would exert if it occupied alone that volume occupied by the mixture at the same temperature.

For a mixture of ideal gases, we have

P = PA + PB + ...... + PK;

where PA is the partial pressure of the species A and so on.

=  PD                       ……….(5.1)

Dalton's law was reformulated by Gibbs to include a second statement on the properties of mixtures. The combined statement is Gibbs-Dalton law:

The internal energy. enthalpy and entropy of a gaseous mixture are respectively equal to the sum of the internal energies, enthalpies, and entropies of the constituents. The internal energy, enthalpy and entropy which a constituent would have if it occupied alone that volume occupied by the mixture at the temperature of the mixture.

Molar Density, Mass Density, Mass Fraction and Mole Fraction

There are a number of ways by which the concentration for a species in a multicomponent mixture can be defined:

(i) Molar Density or Molar Concentration, CA = number of moles of the species A per unit volume of mixture, kg-mol/m3

A = mass of the species A per unit volume of the mixture, kg/m3.

(iii) Mass Fraction, mA = mass concentration of component A / total mass density of the

mixture.

(iv) Mole Fraction, XA = number of moles of species A / total number of moles of the mixture. = CA/C

Therefore, the following summation rules hold true:

CA + CB + .... + CK = C

CA + CB + .... + CK = C

XA + XB + ..... + XK = I1

rnA + mB + ..... + mK  = I                    (5.2)

Since the number of moles = mass of species/molecular weight, we have

C AA  = r/ MA

For a perfect gas, we have:

PA V =n A R oT , where Ro is the universal gas constant,

and,  CA =n A / V  =PA / R oT

X A =CA / C  =PA / P and C =p / R oT

 Mass Average and Molar Average Velocities and Different Types of Fluxes Velocity

In a multicomponent mixture, the bulk velocity of the mixture can be defined on the basis of mass average or molar average velocity. Let VA       A is the mass density of the species A, then the mass average velocity would be:

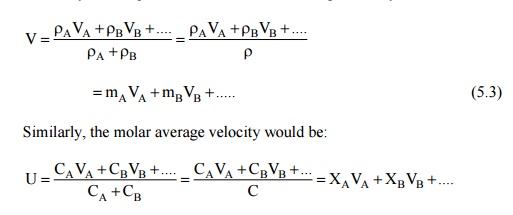
Since mass transfer requires the diffusion of a species with respect to a plane moving with an average velocity, diffusion will take place when the diffusion velocity is in excess of the average velocity. Thus

        Mass diffusion velocity of the species A : VA –V         (5.4)

        Molar diffusion velocity of the species A : VA - U        (5.5)

Fluxes: The mass flux of species A can be expressed relative to either a fixed observer or an observer moving with the bulk velocity. For a stationary observer, the absolute flux of any species A will be equal to the sum of the flux due to the molecular diffusion and that due to the bulk motion.

Similarly, molar diffusion flux = CA(VA –V)