Solved Problems: Dynamics of Machines - Balancing

SOLVED PROBLEMS

1. A shaft has three eccentrics, each 75 mm diameter and 25 mm thick, machined in one piece with the shaft. The central planes of the eccentric are 60 mm apart. The distance of the centres from the axis of rotation are 12 mm, 18 mm and 12 mm and their angular positions are 120° apart. The density of metal is 7000 kg/m³. Find the amount of out-of-balance force and couple at 600 r.p.m. If the shaft is balanced by adding two masses at a radius 75 mm and at distances of 100 mm from the central plane of the middle eccentric, find the amount of the masses and their angular positions.

Let L and M be the planes at distances of 100 mm from the central plane of middle eccentric. The position of the planes and the angular position of the three eccentrics is shown in Fig. 21.12 (a) and (b) respectively. Assuming L as the reference plane and mass of the eccentric A in the vertical direction, the data may be tabulated as below :

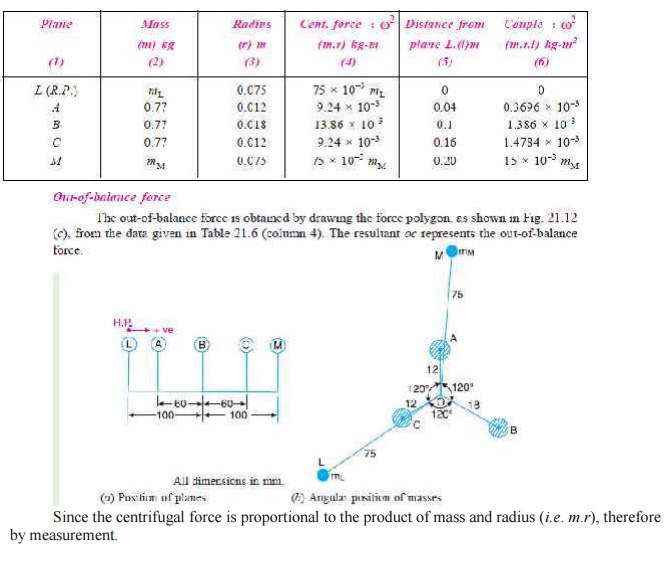
Out-of-balance force = vector oc = 4.75 × 10^–3 kg-m

= 4.75 × 10^–3 × ω ²  = 4.75 × 10^–3 (62.84)² = 18.76 N Ans.

Out-of-balance couple

The out-of-balance couple is obtained by drawing the couple polygon from the data given in Table 21.6 (column 6), as shown in Fig. 21.12 (d). The resultant o ′ c′ represents the out-of- balance couple. Since the couple is proportional to the product of force and distance (m.r.l), there-fore by measurement,

Amount of balancing masses and their angular positions

The vector c ′ o′ (in the direction from c′ to o′ ), as shown in Fig. 21.12 (d) represents the balancing couple and is proportional to 15 × 10^–3 m_M, i.e.

15 × 10^–3 m_M = vector c ′  o′  = 1.1 × 10^–3 kg-m²

m_M = 0.073 kg Ans.

Draw OM in Fig. 21.12 (b) parallel to vector c ′ o′ . By measurement, we find that the angular position of balancing mass (m_M) is 5° from mass A in the clockwise direction. Ans.

In order to find the balancing mass (m_L), a force polygon as shown in Fig. 21.12 (e) is drawn. The closing side of the polygon i.e. vector do (in the direction from d to o) represents the balancing force and is proportional to 75 × 10^–3 m_L. By measurement, we find that,

75 × 10^–3 m_L = vector do = 5.2 × 10^–3 kg-m or m_L = 0.0693 kg Ans. Draw OL in Fig. 21.12 (b), parallel to vector do.

By measurement, we find that the angular position of mass (m_L) is 124° from mass A in the clockwise direction. Ans.

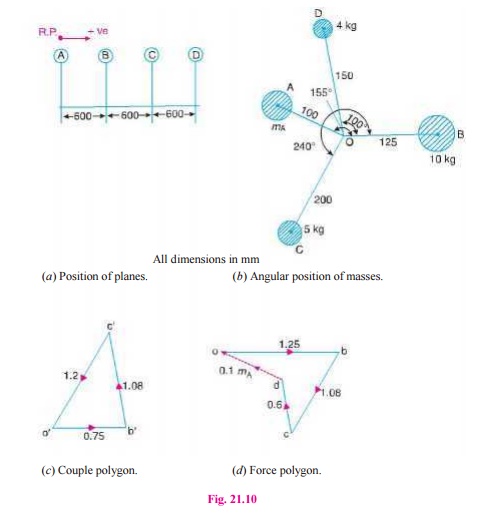
2.(i) A, B, C and D are four masses carried by a rotating shaft at radii 100, 125, 200 and 150 mm respectively. The planes in which the masses revolve are spaced 600 mm apart and the mass of B, C and D are 10 kg, 5 kg, and 4 kg respectively.Find the required mass A and the relative angular settings of the four masses so that the shaft shall be in complete balance.

Solution. Given : r_A = 100 mm = 0.1 m ; r_B = 125 mm = 0.125 m ; r_C = 200 mm = 0.2 m ; r_D = 150 mm = 0.15 m ; m_B = 10 kg ; m_C = 5 kg ; m_D = 4 kg

1. The position of planes is shown in Fig. 21.10 (a). Assuming the plane of mass A as the reference plane (R.P.), the data may be tabulated as below :

First of all, the angular setting of masses C and D is obtained by drawing the couple polygon from the data given in Table 21.4 (column 6). Assume the position of mass B in the horizontal direction OB as shown in Fig. 21.10 (b). Now the couple polygon as shown in Fig.(c) is drawn as discussed below :

direction, i.e. ∠     BOC = 240° Ans.

and angular setting of mass D from mass B in the anticlockwise direction, i.e. ∠ BOD = 100°

Ans.

In order to find the required mass A (m_A) and its angular setting, draw the force polygon to some suitable scale, as shown in Fig. 21.10 (d), from the data given in Table 21.4 (column 4).

Since the closing side of the force polygon (vector do) is proportional to 0.1 m_A, therefore

by measurement,

0.1 m  = 0.7 kg-m²           or  mA= 7 kg Ans.

Now draw OA in Fig. 21.10 (b ), parallel to vector do. By measurement, we find that the angular setting of mass A from mass B in the anticlockwise direction, i.e.

∠       BOA = 155° Ans.

2(ii) Derives the expressions for the following: (i) Variation in tractive force and (ii) Swaying couple. (8) (AU-NOV/DEC-2009)

Variation in tractive force

The resultant unbalanced force due to the two cylinders, along the line of stroke, is known as tractive force. Let the crank for the first cylinder be inclined at an angle θ with the line of stroke, as shown in Fig. 22.4.

Since the crank for the second cylinder is at right angle to the first crank, therefore the angle of inclination for the second crank will be (90° + θ ).

Let m = Mass of the reciprocating parts per cylinder, and 

c = Fraction of the reciprocating parts to be balanced.

We know that unbalanced force along the line of stroke for cylinder 1

The unbalanced forces along the line of stroke for the two cylinders constitute a couple about the centre line YY between the cylinders as shown in Fig. 22.5.

This couple has swaying effect about a vertical axis, and tends to sway the engine alternately in clockwise and anticlockwise directions. Hence the couple is known as swaying couple.

a = Distance between the centre lines of the two cylinders.

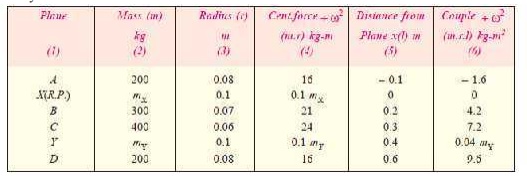
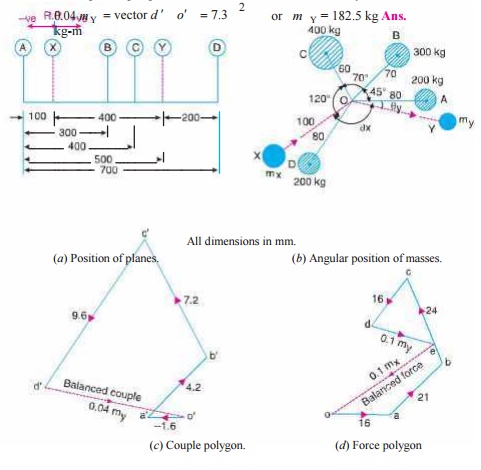
3. A shaft carries four masses A, B, C and D of magnitude 200 kg, 300 kg, 400 kg and 200 kg respectively and revolving at radii 80 mm, 70 mm, 60 mm and 80 mm in planes measured from A at 300 mm, 400 mm and 700 mm. The angles between the cranks measured anticlockwise are A to B 45°, B to C 70° and C to D 120°. The balancing masses are to be placed in planes X and Y. The distance between the planes A and X is 100 mm, between X and Y is 400 mm and between Y and D is 200 mm. If the balancing masses revolve at a radius of 100 mm, find their magnitudes and angular positions.

Solution. Given : m_A = 200 kg ; m_B = 300 kg ; m_C = 400 kg ; m_D = 200 kg ; r_A = 80 mm =0.08m

;

r_B = 70 mm = 0.07 m ; r_C = 60 mm = 0.06 m ; r_D = 80 mm = 0.08 m ; r_X = r_Y = 100 mm = 0.1 m Let m_X = Balancing mass placed in plane X, and m_Y = Balancing mass placed in plane Y.

The position of planes and angular position of the masses (assuming the mass A as horizontal) are shown in Fig. 21.8 (a) and (b) respectively.

Assume the plane X as the reference plane (R.P.). The distances of the planes to the right of plane X are taken as + ve while the distances of the planes to the left of plane X are taken as – ve. The data may be tabulated as shown in Table 21.2.

The balancing masses m_X and m_Y and their angular positions may be determined graphi-cally as discussed below :

1. First of all, draw the couple polygon from the data given in Table 21.2 (column 6) as shown in Fig. 21.8 (c) to some suitable scale. The vector d ′ o′ represents the balanced couple. Since the balanced couple is proportional to 0.04 m_Y, therefore by measurement,

The angular position of the mass m_Y is obtained by drawing Om_Y in Fig. 21.8 (b), parallel to vector d ′ o′ . By measurement, the angular position of m_Y is θ _Y = 12^oin the clockwise direction from mass m_A

(i.e. 200 kg ). Ans.

2. Now draw the force polygon from the data given in Table 21.2 (column 4) as shown in Fig. 21.8 (d). The vector eo represents the balanced force. Since the balanced force is proportional to 0.1 m_X, therefore by measurement,

0.1 m_X = vector eo = 35.5 kg-m      or      m_X = 355 kg Ans.

The angular position of the mass m_X is obtained by drawing Om_X in Fig. 21.8 (b), parallel to vector eo. By measurement, the angular position of m_X is θ _X = 145o in the clockwise direction from mass m_A

(i.e. 200 kg ). Ans.

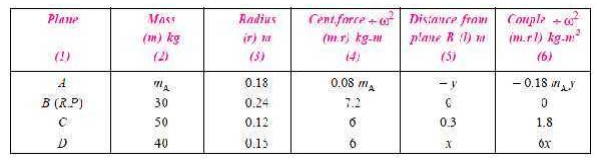
4. Four masses A, B, C and D as shown below are to be completely balanced.

The planes containing masses B and C are 300 mm apart. The angle between planes containing B and C is 90°. B and C make angles of 210° and 120° respectively with D in the same sense. Find :

1.           The magnitude and the angular position of mass A ; and

2.           The position of planes A and D.

Solution. Given : r_A = 180 mm = 0.18 m ; m_B = 30 kg ; r_B = 240 mm = 0.24 m ; m_C = 50 kg ; r_C = 120 mm = 0.12 m ; m_D = 40 kg ; r_D = 150 mm = 0.15 m ;

∠ BOC = 90° ; ∠ BOD = 210° ; ∠ COD = 120°

1. The magnitude and the angular position of mass A

Let m_A = Magnitude of Mass A,

x = Distance between the planes B and D, and y = Distance between the planes A and B.

The position of the planes and the angular position of the masses is shown in Fig. 21.9 (a) and (b) respectively.

Assuming the plane B as the reference plane (R.P.) and the mass B (m_B) along the horizon-tal line as shown in Fig. 21.9 (b), the data may be tabulated as below :

The magnitude and angular position of mass A may be determined by drawing the force polygon from the data given in Table 21.3 (Column 4), as shown in Fig. 21.9 (c), to some suitable scale. Since the masses are to be completely balanced, therefore the force polygon must be a closed figure. The closing side (i.e. vector do) is proportional to 0.18 m_A. By measurement,

0.18 m_A = Vector do = 3.6 kg-m  or  m_A = 20 kg Ans.

In order to find the angular position of mass A, draw OA in Fig. 21.9 (b) parallel to vector do. By measurement, we find that the angular position of mass A from mass B in the anticlockwise direction is  ∠       AOB = 236° Ans.

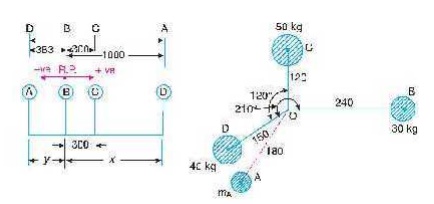
All dimensions in mm.

(c) Force polygon.                        (d) Couple polygon.

Fig. 21.9.

2. Position of planes A and D

The position of planes A and D may be obtained by drawing the couple polygon, as shown in Fig. 21.9 (d), from the data given in Table 21.3 (column 6). The couple polygon is drawn as discussed below :

1.Draw vector o′  c′   parallel to OC and equal to 1.8 kg-m², to some suitable scale.

2.From points c′ and o′ , draw lines parallel to OD and OA respectively, such that they intersect at point d′ . By measurement, we find that

6 x = vector c′     d′         = 2.3 kg-m² or x = 0.383 m

We see from the couple polygon that the direction of vector  c ′       d′       is opposite to the

direction of mass D. Therefore the plane of mass D is 0.383 m or 383 mm towards left of plane B and not towards right of plane B as already assumed. Ans.

Again by measurement from couple polygon,

– 0.18 m_A.y = vector o′  d′  = 3.6 kg-m²

– 0.18 × 20 y = 3.6  or  y = – 1 m

The negative sign indicates that the plane A is not towards left of B as assumed but it is 1 m or 1000 mm towards right of plane B. Ans.

5. An inside cylinder locomotive has its cylinder centre lines 0.7 m apart and has a stroke of 0.6 m. The rotating masses per cylinder are equivalent to 150 kg at the crank pin, and the reciprocating masses per cylinder to 180 kg. The wheel centre lines are 1.5 m apart. The cranks are at right angles.

The whole of the rotating and 2/3 of the recipro-cating masses are to be balanced by masses placed at a radius of 0.6 m. Find the magnitude and direction of the balancing masses.

Find the fluctuation in rail pressure under one wheel, variation of tractive effort and the magnitude of swaying couple at a crank speed of 300 r.p.m. (AU-NOV/DEC-2008)

Solution. Given : a = 0.7 m; l_B = l_C = 0.6 m or

r_B = r_C = 0.3 m; m₁ = 150 kg; m₂ = 180 kg; c = 2/3; r_A = r_D = 0.6 m; N = 300 r.p.m. or ω  2 300 / 60 = 31.42 rad/s

We know that the equivalent mass of the rotating parts to be balanced per cylinder at the crank

pin,

m = m_B = m_C = m₁ + c.m₂ = 150 + ^2/₃ × 180 = 270 kg

Magnitude and direction of the balancing masses

Let m_A and m_D = Magnitude of the balancing masses

θ  _A and θ  _D = Angular position of the balancing masses m_A and m_D from the first crank B.

The magnitude and direction of the balancing masses may be determined graphically as discussed below :

1. First of all, draw the space diagram to show the positions of the planes of the wheels and the cylinders, as shown in Fig. 22.7 (a). Since the cranks of the cylinders are at right angles, therefore assuming the position of crank of the cylinder B in the horizontal direc-tion, draw OC and OB at right angles to each other as shown in Fig. 22.7 (b).

Tabulate the data as given in the following table. Assume the plane of wheel A as the reference plane.

3. Now, draw the couple polygon from the data given in Table 22.1 (column 6), to some suitable

scale, as shown in Fig 22.7 (c). The closing side c ′o′ represents the balancing couple and it is proportional to 0.9 m_D. Therefore, by measurement,

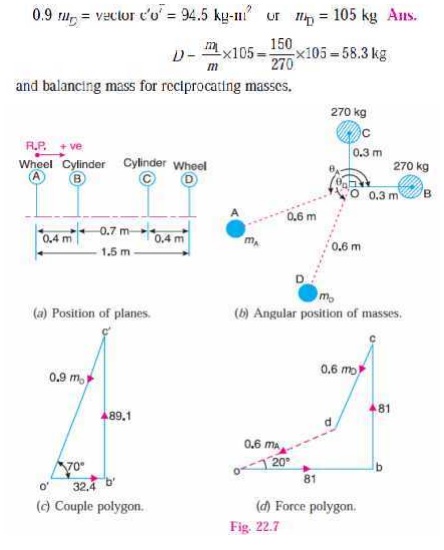
4. To determine the angular position of the balancing mass D, draw OD in Fig. 22.7 (b) parallel to vector c ′ o′ . By measurement,

θ      _D  = 250°

Ans.

5. In order to find the balancing mass A, draw the force polygon from the data given in

Table 22.1 (column 4), to some suitable scale, as shown in Fig. 22.7 (d), The vector do represents the balancing force and it is proportional to 0.6 m_A. Therefore by measurement,

0.6        m_A = vector do = 63 kg-m or m_A = 105 kg Ans.

6. To determine the angular position of the balancing mass A, draw OA in Fig. 22.7 (b) parallel to vector do. By measurement,

θ     _A  = 200°

Ans.

Fluctuation in rail pressure

We know that each balancing mass105 kg

∴       Balancing mass for rotating masses,

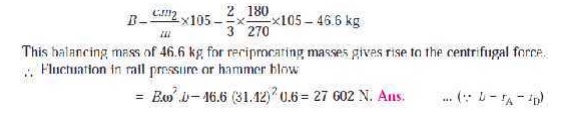
Variation of tractive effort

We know that maximum variation of tractive effort

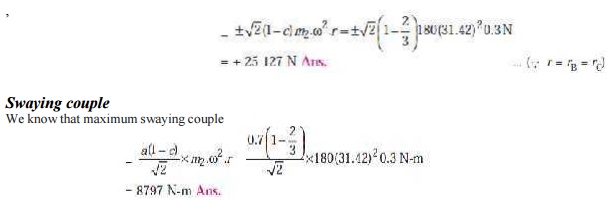
6. The following data apply to an outside cylinder uncoupled locomotive :

Mass of rotating parts per cylinder = 360 kg ; Mass of reciprocating parts per cylinder = 300 kg ; Angle between cranks = 90° ; Crank radius = 0.3 m ; Cylinder centres = 1.75 m ; Radius of balance masses = 0.75 m ; Wheel centres = 1.45 m. If whole of the rotating and two-thirds of reciprocating parts are to be balanced in planes of the driving wheels, find :

1.                   Magnitude and angular positions of balance masses,

2.                   Speed in kilometres per hour at which the wheel will lift off the rails when the load on each driving wheel is 30 kN and the diameter of tread of driving wheels is 1.8 m, and

3. Swaying couple at speed arrived at in (2) above.

Solution : Given : m₁ = 360 kg ; m₂ = 300 kg ; ∠ AOD = 90° ; r_A = r_D = 0.3 m ; a = 1.75 m ; r_B = r_C = 0.75 m ; c = 2 / 3.

We know that the equivalent mass of the rotating parts to be balanced per cylinder,

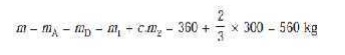
1. Magnitude and angular position of balance masses

Let    m_B and m_C = Magnitude of the balance masses, and θ_B and θ _C = angular position of the balance masses m_B and m_C from the crank A.

The magnitude and direction of the balance masses may be determined, graphically, as discussed below :

First of all, draw the positions of the planes of the wheels and the cylinders as shown in Fig. 22.11 (a). Since the cranks of the two cylinders are at right angles, therefore assum-ing the position of the cylinder A in the horizontal direction, draw OA and OD at right angles to each other as shown in Fig. 22.11 (b).

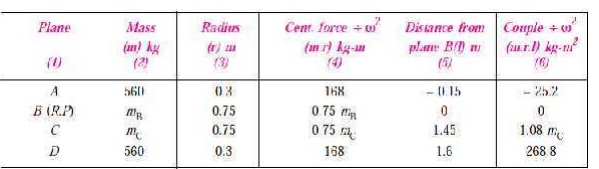
2. Assuming the plane of wheel B as the reference plane, the data may be tabulated as be-low:

3. Now draw the couple polygon with the data given in Table 22.4 column (6), to some suitable scale as shown in Fig. 22.11(c). The closing side d ′ o′ represents thebalancing couple and it is proportional to 1.08 m_C. Therefore, by measurement,

4. To determine the angular     position of the balancing mass C, draw OC parallel to vector d′  o′  as shown in Fig. 22.11       (b). By measurement, θ C = 275° Ans.

5. In order to find the balancing mass B, draw the force polygon with the data given in Tablecolumn (4), to some suitable scale, as shown in Fig. 22.11 (d). The vector co represents

the balancing force and it is proportional to 0.75 m_B. Therefore, by measurement, 0.75 m_B = 186.75 kg-m or m_B = 249 kg Ans.

4.           To determine the angular position of the balancing mass B, draw OB parallel to vector oc as shown Fig. 22.11 (b). By measurement, θ        _B = 174.5° Ans.

2. Speed at which the wheel will lift off the rails

Given :      P = 30 kN = 30 × 10³ N ; D = 1.8 m

Let ω = Angular speed at which the wheels will lift off the rails in rad/s, and v = Corresponding linear speed in km/h.

We know that each balancing mass, m_B = m_C = 249 kg

∴       Balancing mass for reciprocating parts,

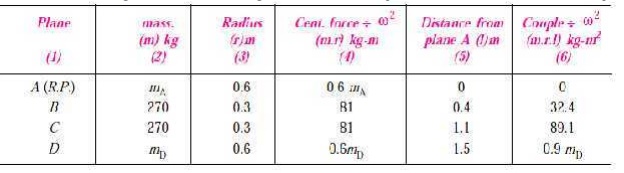
7.       The three cranks of a three cylinder locomotive are all on the same axle and are set at 120°. The pitch of the cylinders is 1 meter and the stroke of each piston is 0.6 m. The reciprocating  masses are 300 kg for inside cylinder and 260 kg for each outside cylinder and the planes of rotation of the balance masses are 0.8 m from the inside crank. If 40% of the reciprocating parts are to be balanced, find :

1. the magnitude and the position of the balancing masses required at a radius of 0.6 m ;

And

2.       the hammer blow per wheel when the axle makes 6 r.p.s.

Solution. Given : ∠          AOB = ∠  BOC = ∠    COA = 120° ; l_A = l_B = l_C = 0.6 m or r_A = r_B

= r_C = 0.3 m ; m_I = 300 kg ; m_O = 260 kg ; c = 40% = 0.4 ; b₁ = b₂ = 0.6 m ; N = 6 r.p.s.

= 6 × 2 π  = 37.7 rad/s

Since 40% of the reciprocating masses are to be balanced, therefore mass of the reciprocat-ing parts to be balanced for each outside cylinder,

m_A = m_C = c × m_O = 0.4 × 260 = 104 kg and mass of the reciprocating parts to be balanced for inside cylinder,

m_B = c × m₁ = 0.4 × 300 = 120 kg

1. Magnitude and position of the balancing masses

Let    B₁ and B₂ = Magnitude of the balancing masses in kg,

θ₁ and θ₂ = Angular position of the balancing masses B₁ and B₂ from crank A.

The magnitude and position of the balancing masses may be determined graphically as discussed below :

1. First of all, draw the position of planes and cranks as shown in Fig. 22.8 (a) and (b) respectively. The position of crank A is assumed in the horizontal direction.

Tabulate the data as given in the following table. Assume the plane of balancing mass B₁ (i.e. plane 1) as the reference plane.

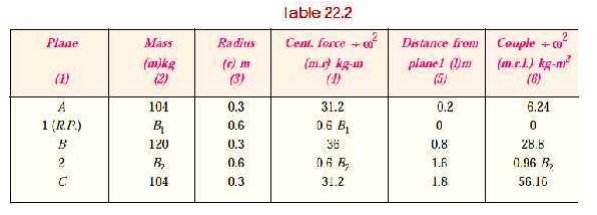
3. Now draw the couple polygon with the data given in Table 22.2 (column 6), to some suitable scale, as shown in Fig. 22.8 (c). The closing side c ′ o′ represents the balancing couple

and it is proportional to 0.96 B₂. Therefore, by measurement,

0.96  B₂ = vector c ′  o′          = 55.2 kg-m² or B₂ = 57.5 kg Ans.

4. To determine the angular position of the balancing mass B₂, draw OB₂ parallel to vector c

′       o′  as shown in Fig. 22.8 (b). By measurement,

θ₂= 24° Ans.

5. In order to find the balance mass B₁, draw the force polygon with the data given in Table 22.2(column 4 ), to some suitable scale, as shown in Fig. 22.8 (d). The closing side co represents the balancing force and it is proportional to 0.6 B₁. Therefore, by measurement,

0.6B₁ = vector co = 34.5 kg-m  or  B₁ = 57.5 kg Ans.

6.To determine the angular position of the balancing mass B₁, draw OB₁ parallel to vector co, as shown in Fig. 22.8 (b). By measurement, θ₁ = 215° Ans.

2. Hammer blow per wheel

We know that hammer blow per wheel

= B₁.ω ².b₁  = 57.5 (37.7)² 20.6 = 49 035 N Ans.

8. The following data refer to two cylinder locomotive with cranks at 90° :

Reciprocating mass per cylinder = 300 kg ; Crank radius = 0.3 m ; Driving wheel diameter = 1.8 m ; Distance between cylinder centre lines = 0.65 m ; Distance between the driving wheel central planes = 1.55 m.

Determine : 1. the fraction of the reciprocating masses to be balanced, if the hammer blow is not to exceed 46 kN at 96.5 km. p.h. ; 2. the variation in tractive effort ; and 3. the maximum swaying couple

Solution. Given : m = 300 kg ; r = 0.3 m ; D = 1.8 m or R = 0.9 m ; a = 0.65 m ; Hammer blow = 46 kN = 46 × 10³ N ; v = 96.5 km/h = 26.8 m/s

1. Fraction of the reciprocating masses to be balanced

Let c = Fraction of the reciprocating masses to be balanced, and

B = Magnitude of balancing mass placed at each of the driving wheels at radius b. We know that the mass of the reciprocating parts to be balanced = c.m = 300c kg

Fig. 22.9

The position of planes of the wheels and cylinders is shown in Fig. 22.9 (a), and the position of

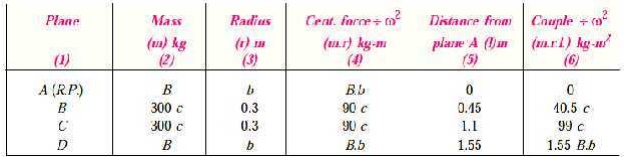
cranks is shown in Fig 22.9 (b). Assuming the plane of wheel A as the reference plane, the data may be tabulated as below :

Now the couple polygon, to some suitable scale, may be drawn with the data given in Table 22.3 (column 6), as shown in Fig. 22.10. The closing side of the polygon (vector c′ o′ ) represents the balancing couple and is proportional to 1.55 B.b. From the couple polygon,

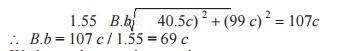
We know that angular speed,

ω  = v/R = 26.8/0.9 = 29.8 rad/s ∴        Hammer

blow,

46 × 10³ = B. ω ² .b

=  69 c (29.8)² = 61 275 c

∴                                            c = 46 × 10³/61 275 = 0.751

Ans.

2. Variation in tractive effort

We know that variation in tractive effort,

3.Maximum swaying couple

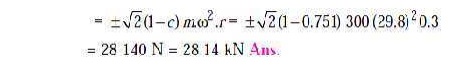
 We know the maximum swaying couple

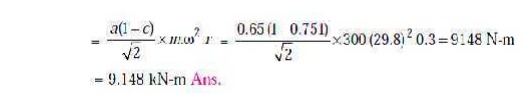
TUTORIAL PROBLEMS:

1.         Four masses A, B, C and D revolve at equal radii and are equally spaced along a shaft. The mass B is 7 kg and the radii of C and D make angles of 90° and 240° respectively with the radius of B. Find the magnitude of the masses A, C and D and the angular position of A so that the system may be completely balanced.

[Ans. 5 kg ; 6 kg ; 4.67 kg ; 205° from mass B in anticlockwise direction]

2. A rotating shaft carries four masses A, B, C and D which are radially attached to it. The mass centres are 30 mm, 38 mm, 40 mm and 35 mm respectively from the axis of rotation. The masses A, C and D are 7.5 kg, 5 kg and 4 kg respectively. The axial distances between the planes of rotation of A and B is 400 mm and between B and C is 500 mm. The masses A and C are at right angles to each other. Find for a complete balance,

1.       the angles between the masses B and D from mass A,

2.       the axial distance between the planes of rotation of C and D,

3.       the magnitude of mass B.[Ans. 162.5°, 47.5° ; 511 mm : 9.24 kg]

3.     A three cylinder radial engine driven by a common crank has the cylinders spaced at 120°. The stroke is 125 mm, length of the connecting rod 225 mm and the mass of the reciprocating parts per cylinder 2 kg. Calculate the primary and secondary forces at crank shaft speed of 1200 r.p.m.

[Ans. 3000 N ; 830 N]

4.     The pistons of a 60° twin V-engine has strokes of 120 mm. The connecting rods driving a common crank has a length of 200 mm. The mass of the reciprocating parts per cylinder is 1 kg and the

speed of the crank shaft is 2500 r.p.m. Determine the magnitude of the primary and secondary forces. [Ans.

6.3            kN ; 1.1 kN]

5.     A twin cylinder V-engine has the cylinders set at an angle of 45°, with both pistons connected to the single crank. The crank radius is 62.5 mm and the connecting rods are 275 mm long. The reciprocating mass per line is 1.5 kg and the total rotating mass is equivalent to 2 kg at the crank radius. A balance mass fitted opposite to the crank, is equivalent to 2.25 kg at a radius of 87.5 mm. Determine for an engine speed of 1800 r.p.m. ; the maximum and minimum values of the primary and secondary forces due to the inertia of reciprocating and rotating masses.

[ Ans. Primary forces : 3240 N (max.) and 1830 N (min.) Secondary forces : 1020 N (max.) and 470 N (min.)]