Single Degree Free Vibration

SINGLE DEGREE FREE VIBRATION

1 INTRODUCTION:

When a system is subjected to an initial disturbance and then left free to vibrate on its own, the resulting vibrations are referred to as free vibrations . Free vibration occurs when a mechanical system is set off with an initial input and then allowed to vibrate freely. Examples of this type of vibration are pulling a child back on a swing and then letting go or hitting a tuning fork and letting it ring. The mechanical system will then vibrate at one or more of its "natural frequencies" and damp down to zero.

2 BASIC ELEMENTS OF VIBRATION SYSTEM:

Mass or Inertia

Springiness or Restoring element

Dissipative element (often called damper)

External excitation

3 CAUSES OF VIBRATION:

Unbalance: This is basically in reference to the rotating bodies. The uneven distribution of mass in a rotating body contributes to the unbalance. A good example of unbalance related vibration would be the ―vibrating alert‖ in our mobile phones. Here a small amount of unbalanced weight is rotated by a motor causing the vibration which makes the mobile phone to vibrate. You would have experienced the same sort of vibration occurring in your front loaded washing machines that tend to vibrate during the ―spinning‖ mode.

Misalignment: This is an other major cause of vibration particularly in machines that are driven by motors or any other prime movers.

Bent Shaft: A rotating shaft that is bent also produces the the vibrating effect since it losses it rotation capability about its center.

Gears in the machine: The gears in the machine always tend to produce vibration, mainly due to their meshing. Though this may be controlled to some extent, any problem in the gearbox tends to get enhanced with ease.

Bearings: Last but not the least, here is a major contributor for vibration. In majority of the cases every initial problem starts in the bearings and propagates to the rest of the members of the machine. A bearing devoid of lubrication tends to wear out fast and fails quickly, but before this is noticed it damages the remaining components in the machine and an initial look would seem as if something had gone wrong with the other components leading to the bearing failure.

Effects of vibration:

(a)Bad Effects:

The presence of vibration in any mechanical system produces unwanted noise, high stresses, poor reliability, wear and premature failure of parts. Vibrations are a great source of human discomfort in the form of physical and mental strains.

(b)Good Effects:

A vibration does useful work in musical instruments, vibrating screens, shakers, relive pain in physiotherapy.

4 METHODS OF REDUCTION OF VIBRATION:

¨     -unbalance is its main cause, so balancing of parts is necessary.

¨     -using shock absorbers.

¨     -using dynamic vibration absorbers.

¨     -providing the screens (if noise is to be reduced)

5 TYPES OF VIBRATORY MOTION:

¨     Free Vibration

¨     Forced Vibration

6 TERMS USED VIBRATORY MOTION:

(a)Time period (or)period of vibration:

It is the time taken by a vibrating body to repeat the motion itself.time period is usually expressed in seconds.

(b) Cycle:

It is the motion completed in one time period.

(c) Periodic motion:

A motion which repeats itself after equal interval of time.

(d)Amplitude (X)

The maximum displacement of a vibrating body from the mean position.it is usually expressed in millimeter.

(e) Frequency (f)

The number of cycles completed in one second is called frequency

7 DEGREES OF FREEDOM:

The minimum number of independent coordinates required to specify the motion of a system at any instant is known as D.O.F of the system.

Single degree of freedom system:

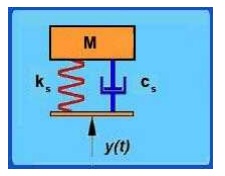
The system shown in this figure is what is known as a Single Degree of Freedom system. We use the term degree of freedom to refer to the number of coordinates that are required to specify completely the configuration of the system. Here, if the position of the mass of the system is specified then accordingly the position of the spring and damper are also identified. Thus we need just one coordinate (that of the mass) to specify the system completely and hence it is known as a single degree of freedom system.

Two degree of freedom system:

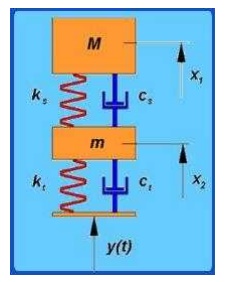
A two degree of freedom system With reference to automobile applications, this is referred as ―quarter car‖ model. The bottom mass refers to mass of axle, wheel etc components which are below the suspension spring and the top mass refers to the mass of the portion of the car and

passenger. Since we need to specify both the top and bottom mass positions to completely specify the system, this becomes a two degree of freedom system.

8 TYPES OF VIBRATORY MOTION:

Types of Vibration:

(a)Longitudinal vibration       (b)Transverse Vibration      ( c)Torsional Vibration.

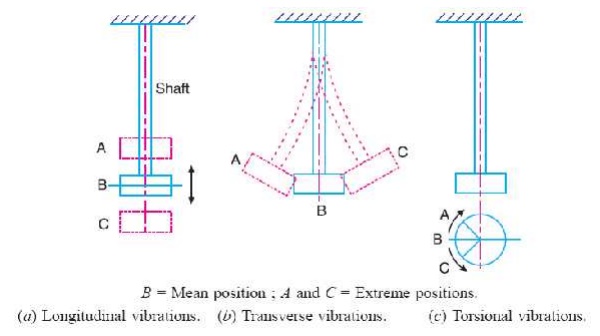
Longitudinal Vibration:

When the particles of the shaft or disc moves parallel to the axis of the shaft, then the vibrations known as longitudinal vibrations.

Free undamped longitudinal vibrations;

When a body is allowed to vibrate on its own, after giving it an initial displacement, then the ensuring vibrations are known as free or natural vibrations. When the vibrations take place parallel to the axis of constraint and no damping is provided, then it is called free undamped longitudinal vibrations.

9 NATURAL FREQUENCY OF FREE UNDAMPED LONGITUDINAL VIBRATION:

Equilibrium method  or Newton ’ s  method :

Energy Method

In free vibrations, no energy is transferred into the system or from the system. Therefore, the total energy (sum of KE and PE)is constant and is same all the times.

3 Rayleigh’s method

In this method, the maximum kinetic energy at mean position is made equal to the maximum potential energy at the extreme position.

10 EQUIVALENT STIFFNESS OF SPRING.

(1) Springs in series

(2) Springs in parallel

(3) Combined springs

(4) Inclined springs

11 DAMPING:

It is the resistance to the motion of a vibrating body. The vibrations associated with this resistance are known as damped vibrations.

Types of damping:

(1) Viscous damping

(2) Dry friction or coulomb damping

(3) Solid damping or structural damping

(4) Slip or interfacial damping.

Damping Coefficient:

The damping force per unit velocity is known as damping coefficient.

Equivalent damping coefficient:

Dampers may be connected either in series or in parallel to provide required damping.

12 DAMPED VIBRATION:

The vibrations associated with this resistance are known as damped vibrations.

Damping factor:

Damping factor can be defined as the ratio of actual damping coefficient to critical damping coefficient.

Logarithmic decrement:

It is defined as the natural logarithm of ratio of any two successive amplitudes of an under damped system. It is a dimensionless quantity.

13 TRANSVERSE VIBRATION:

When the particles of the shaft or disc moves approximately perpendicular to the axis of the shaft, then the vibrations known as transverse vibrations.

Whirling speed of shaft:

The speed, at which the shaft runs so that the additional deflection of the shaft from the axis of rotation becomes infinite, is known as critical or whirling speed.

No shaft can ever be perfectly straight or perfectly balanced. When an element of mass is a distance from the axis of rotation, centrifugal force, will tend to pull the mass outward. The elastic properties of the shaft will act to restore the ―straightness‖. If the frequency of rotation is equal to one of the resonant frequencies of the shaft, whirling will occur. In order to save the machine from failure, operation at such whirling speeds must be avoided.

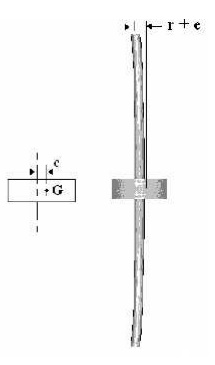
The whirling frequency of a symmetric cross section of a given length between two points is

given by:

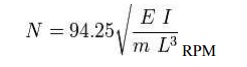
Where E = young's modulus, I = Second moment of area, m = mass of the shaft, L= length of the shaft between points

A shaft with weights added will have an angular velocity of N (rpm) equivalent as follows:

14 TORSIONAL VIBRATION:

When the particles of the shaft or disc move in a circle about the axis of the shaft, then the vibrations known as tensional vibration

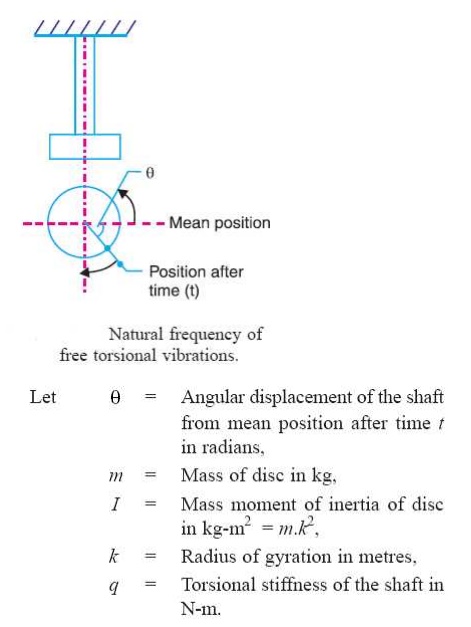
Torsional vibration of a single rotor system:

Torsional vibration of a two rotor system:

Torsionally equivalent shaft: