Solved Problems: Single Degree Free Vibration

SOLVED PROBLEMS

1. A machine of mass 75 kg is mounted on springs and is fitted with a dashpot to damp out vibrations. There are three springs each of stiffness 10 N/mm and it is found that the amplitude of vibration diminishes from 38.4 mm to 6.4 mm in two complete oscillations. Assuming that the damping force varies as the velocity, determine : 1. the resistance of the dash-pot at unit velocity ; 2. the ratio of the frequency of the damped vibration to the frequency of the undamped vibration ; and 3. the periodic time of the

damped vibration.

Solution. Given : m = 75 kg ; s = 10 N/mm = 10 ×10³ N/m ; x1 = 38.4 mm = 0.0384 m ; x3 = 6.4 mm = 0.0064 m

Since the stiffness of each spring is 10 × 10³ N/m and there are 3 springs, therefore total stiffness,

1.  Resistance of the dashpot at unit velocity

2. Ratio of the frequency of the damped vibration to the frequency of undamped vibration

2.     The mass of a single degree damped vibrating system is 7.5 kg and makes 24 free oscillations in 14 seconds when disturbed from its equilibrium position. The amplitude of vibration reduces to 0.25 of its initial value after five oscillations. Determine : 1. stiffness of the spring, 2. logarithmic decrement, and 3. damping factor, i.e. the ratio of the system damping to critical damping.

Solution. Given : m = 7.5 kg

Since 24 oscillations are made in 14 seconds, therefore frequency of free vibrations,

3(i) The measurements on a mechanical vibrating system show that it has a mass of 8 kg and that the springs can be combined to give an equivalent spring of stiffness 5.4 N/mm. If the vibrating system have a dashpot attached which exerts a force of 40 N when the mass has a velocity of 1 m/s, find : 1. critical damping coefficient, 2. damping factor, 3. logarithmic decrement, and 4. ratio of two consecutive amplitudes.

Solution. Given : m = 8 kg ; s = 5.4 N/mm = 5400 N/m

Since the force exerted by dashpot is 40 N, and the mass has a velocity of 1 m/s , therefore Damping coefficient (actual),

3 (ii) An instrument vibrates with a frequency of 1 Hz when there is no damping. When the damping is provided, the frequency of damped vibrations was observed to be 0.9 Hz. Find 1. the damping factor, and 2. logarithmic decrement.

Solution. Given : fn = 1 Hz ; fd = 0.9 Hz

1. Damping factor

Let  m =      Mass of the instrument in kg,

       c =       Damping coefficient or damping force per unit

       c_c=       velocity in N/m/s, and Critical damping coefficient in N/m/s.

We know that natural circular frequency of undamped vibrations,

4(i) A coil of spring stiffness 4 N/mm supports vertically a mass of 20 kg at the free end. The motion is resisted by the oil dashpot. It is found that the amplitude at the beginning of the fourth cycle is 0.8 times the amplitude of the previous vibration. Determine the damping force per unit velocity. Also find the ratio of the frequency of damped and undamped vibrations.

Solution. Given : s = 4 N/mm = 4000 N/m ; m = 20 kg

Damping force per unit velocity

Let c = Damping force in newtons per unit velocity i.e. in N/m/s

xn = Amplitude at the beginning of the third cycle,

xn+1 = Amplitude at the beginning of the fourth cycle = 0.8 xn We know that natural circular frequency of motion,

4(ii) Derive an expression for the natural frequency of single degrees of freedom system.

We know that the kinetic energy is due to the motion of the body and the potential energy is with respect to a certain datum position which is equal to the amount of work required to move the body from the datum position. In the case of vibrations, the datum position is the mean or equilibrium position at which the potential energy of the body or the system is zero.

In the free vibrations, no energy is transferred to the system or from the system. Therefore the summation of kinetic energy and potential energy must be a constant quantity which is same at all the times. In other words,

5. A vertical shaft of 5 mm diameter is 200 mm long and is supported in long bearings at its ends. A disc of mass 50 kg is attached to the centre of the shaft. Neglecting any increase in stiffness due to the attachment of the disc to the shaft, find the critical speed of rotation and the maximum bending stress when the shaft is rotating at 75% of the critical speed. The centre of the disc is 0.25 mm from the geometric axis of the shaft. E = 200 GN/m².

Solution. Given : d = 5 mm = 0.005 m ; l = 200 mm = 0.2 m ; m = 50 kg ; e = 0.25 mm = 0.25 × 10^–3 m ; E = 200 GN/m² = 200 × 10⁹ N/m²

Critical speed of rotation

We know that moment of inertia of the shaft,

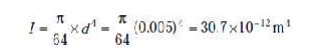
Since the shaft is supported in long bearings, it is assumed to be fixed at both ends. We know that the static deflection at the centre of the shaft due to a mass of 50 kg,

Maximum bending stress

Let σ = Maximum bending stress in N/m², and

N = Speed of the shaft = 75% of critical speed = 0.75 Nc . . . (Given)

When the shaft starts rotating, the additional dynamic load (W1) to which the shaft is subjected, may be obtained by using the bending equation,

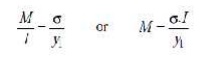
We know that for a shaft fixed at both ends and carrying a point load (W1) at the centre, the maximum bending moment

6.(i) A shaft 50 mm diameter and 3 metres long is simply supported at the ends and carries three loads of 1000 N, 1500 N and 750 N at 1 m, 2 m and 2.5 m from the left support. The Young's modulus for shaft material is 200 GN/m². Find the frequency of transverse vibration.

Solution. Given : d = 50 mm = 0.05 m ; l = 3 m, W1 = 1000 N ; W2 = 1500 N ; W3 = 750 N; E = 200 GN/m² = 200 × 10⁹ N/m²

The shaft carrying the loads is shown in Fig. 23.13 We know that moment of inertia of the shaft,

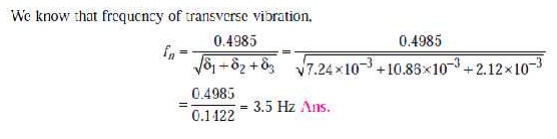
6.(ii) Calculate the whirling speed of a shaft 20 mm diameter and 0.6 m long carrying a mass of 1 kg at its mid-point. The density of the shaft material is 40 Mg/m³, and Young’s modulus is 200 GN/m². Assume the shaft to be freely supported.

TUTORIAL PROBLEMS

1.     A beam of length 10 m carries two loads of mass 200 kg at distances of 3 m from each end together with a central load of mass 1000 kg. Calculate the frequency of transverse vibrations. Neglect the mass of the beam and take I = 10⁹ mm⁴ and E = 205×10 ³ N/mm². [Ans. 13.8 Hz]

13.8             

2.          A vertical shaft 25 mm diameter and 0.75 m long is mounted in long bearings and carries

a pulley

of mass 10 kg midway between the bearings. The centre of pulley is 0.5 mm from the axis of the shaft. Find (a) the whirling speed, and (b) the bending stress in the shaft, when it is rotating at 1700 r.p.m. Neglect the mass of the shaft and E = 200 GN/m².

[Ans. 3996 r.p.m ; 12.1 MN/m²]

3. A shaft of 100 mm diameter and 1 metre long is fixed at one end and the other end carries a

flywheel of mass 1 tonne. The radius of gyration of the flywheel is 0.5 m. Find the frequency of torsional vibrations, if the modulus of rigidity for the shaft material is 80 GN/m². [Ans. 8.9 Hz]

4.The two rotors A and B are attached to the end of a shaft 500 mm long. The mass of the rotor A is 300 kg and its radius of gyration is 300 mm. The corresponding values of the rotor B are 500 kg and 450 mm respectively. The shaft is 70 mm in diameter for the first 250 mm ; 120 mm for the next 70 mm and 100 mm diameter for the remaining length. The modulus of rigidity for the shaft material is 80 GN/m². Find : 1. The position of the node, and 2. The frequency of torsional vibration. [Ans. 225 mm from A ; 27.3 Hz]