Important Short Questions and Answers: Single Degree Free Vibration

SINGLE DEGREE FREE VIBRATION

1.    How will you classify vibration? (Or) what are the different type f vibratory motions?

•      Free vibrations

•      Longitudinal vibration,

•      Transverse vibration, and

•      Torsional vibration.

•      Forced vibrations, and

•      Damped vibration.

2.    What are the causes and effect of vibration?

The causes of vibration are unbalanced forces, elastic nature of the system, self excitation, wind and earthquakes.

The existence of vibration elements in any mechanical system produces unwanted noise, high stress, poor reliability and premature failure of one or more of the parts.

3.    What do you mean by a degree of freedom or movability?

The number of independent coordinates required to completely define the motion of a system is known as degree of freedom of the system.

4.    What is the limit beyond which damping is detrimental and why?

When damping factor x > 1, the aperiodic motion is resulted. That is, aperiodic motion means the system cannot vibrate due to over damping. Once the system is disturbed, it will take infinite time to come back to equilibrium position.

5.    What is meant by critical damping?

The system is said to be critically damped when the damping factor Ϛ = 1. If the system is critically damped, the mass moves back very quickly to its equilibrium position within no time.

6.    Define critical or whirling or whipping speed of a shaft? Give one application of critical damping.

The speed at which resonance occurs is called critical speed of the shaft . In other words, the speed at which the shaft runs so that the additional deflection of the shaft from the axis of rotation becomes infinite is known as critical speed.

The property of critical damping is used in designing elecrical instruments, hydraulic door closers and large guns.

7.    What are the factors that affect the critical speed of a shaft?

The critical speed essentially depends on:

•      The eccentricity of the C.G of the rotating masses from the axis of rotation of the shaft,

•      Diameter of the disc,

•      Span of the shaft, and

•      Type of supports connections at its ends.

8.    What is the effect of inertia on the shaft in longitudinal and transverse vibrations?

In longitudinal vibrations, he inertia effect of the shaft is equal to the that of a mass one third of the mass of the shaft concentrated at its free end.

9.    Define logarithmic decrement.

Logarithmic decrement is defined as the natural logarithm of the amplitude reduction factor. The amplitude reduction factor is the ratio of any two successive amplitudes on the same side of the mean position.

10.  Define damping factor and damping co-efficient.

• The damping factor or damping ratio is defined as the ratio of actual damping coefficient (c) to the critical damping co-efficient(c_c).

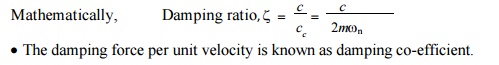
11.  Define node in torsional vibration. (or) what is nodal section in two rotor system.

Node is the point or the section of the shaft at which amplitude of the torsional vibration is zero. At nodes, the shaft remains unaffected by the vibration.

12.  What is difference between damping, viscous damping and Coloumb damping?

•      Damping: The resistance against the vibration is called damping.

•      Viscous Damping is the damping provided by fluid resistance.

•      Coloumb damping is the dampin results from two dry or unlubricated surfaces rubbing together.

13.  Define torsional equivalent shaft?

A shaft having diameter for different lengths can be theoretically replaced by an equivalent shaft of uniform diameter such that they have the same total angle of twist when equal opposing torques are applied at their ends. Such a theoretically replaced shaft is known as torsion ally equivalent shaft.

14.  Determine the natural frequency of mass of 10kgsuspended at the bottom of two springs of stiffness: 5 N/mm and 8 N/mm in series.

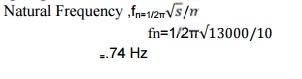
15.  State natural frequency of torsional vibration of a simple system?

Natural frequency of torsional vibration,

Where C = Rigidity modulus of shaft, I = Mass M.I. of rotor, J = polar M.I of shaft, and

l = Length of node from rotor.