Forced Vibration

FORCED VIBRATION

1 INTRODUCTION:

When a system is subjected continuously to time varying disturbances, the vibrations resulting under the presence of the external disturbance are referred to as forced vibrations.

Forced vibration is when an alternating force or motion is applied to a mechanical system. Examples of this type of vibration include a shaking washing machine due to an imbalance, transportation vibration (caused by truck engine, springs, road, etc), or the vibration of a building during an earthquake. In forced vibration the frequency of the vibration is the frequency of the force or motion applied, with order of magnitude being dependent on the actual mechanical system.

When a vehicle moves on a rough road, it is continuously subjected to road undulations causing the system to vibrate (pitch, bounce, roll etc). Thus the automobile is said to undergo forced vibrations. Similarly whenever the engine is turned on, there is a resultant residual unbalance force that is transmitted to the chassis of the vehicle through the engine mounts, causing again forced vibrations of the vehicle on its chassis. A building when subjected to time varying ground motion (earthquake) or wind loads, undergoes forced vibrations. Thus most of the practical examples of vibrations are indeed forced vibrations.

2 CAUSES RESONANCE:

Resonance is  simple to  understand  if  you  view the spring and  mass  as  energy storage

elements – with the mass storing kinetic energy and the spring storing potential energy. As discussed earlier, when the mass and spring have no force acting on them they transfer energy back and forth at a rate equal to the natural frequency. In other words, if energy is to be efficiently pumped into both the mass and spring the energy source needs to feed the energy in at a rate equal to the natural frequency. Applying a force to the mass and spring is similar to pushing a child on swing, you need to push at the correct moment if you want the swing to get higher and higher. As in the case of the swing, the force applied does not necessarily have to be high to get large motions; the pushes just need to keep adding energy into the system.

The damper, instead of storing energy, dissipates energy. Since the damping force is proportional to the velocity, the more the motion, the more the damper dissipates the energy. Therefore a point will come when the energy dissipated by the damper will equal the energy being fed in by the force. At this point, the system has reached its maximum amplitude and will continue to vibrate at this level as long as the force applied stays the same. If no damping exists, there is nothing to dissipate the energy and therefore theoretically the motion will continue to grow on into infinity.

3 FORCED VIBRATION OF A SINGLE DEGREE-OF-FREEDOM SYSTEM:

We saw that when a system is given an initial input of energy, either in the form of an initial displacement or an initial velocity, and then released it will, under the right conditions, vibrate freely. If there is damping in the system, then the oscillations die away. If a system is given a continuous input of energy in the form of a continuously applied force or a continuously applied displacement, then the consequent vibration is called forced vibration. The energy input can overcome that dissipated by damping mechanisms and the oscillations are sustained.

We will consider two types of forced vibration. The first is where the ground to which the system is attached is itself undergoing a periodic displacement, such as the vibration of a building in an earthquake. The second is where a periodic force is applied to the mass, or object performing the motion; an example might be the forces exerted on the body of a car by the forces produced in the engine. The simplest form of periodic force or displacement is sinusoidal, so we will begin by considering forced vibration due to sinusoidal motion of the ground. In all real systems, energy will be dissipated, i.e. the system will be damped, but often the damping is very small. So let us first analyze systems in which there is no damping.

4 STEADY STATE RESPONSE DUE TO HARMONIC OSCILLATION:

Consider a spring-mass-damper system as shown in figure 4.1. The equation of motion of this system subjected to a harmonic force Fsin(wt) can be given by

where, m , k and c are the mass, spring stiffness and damping coefficient of the system, F is the amplitude of the force, w is the excitation frequency or driving frequency.

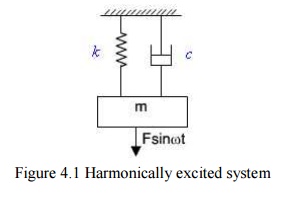
Figure 4.1 Harmonically excited system

Figure 4.2: Force polygon

The steady state response of the system can be determined by solving equation(4.1) in many different ways. Here a simpler graphical method is used which will give physical understanding to this dynamic problem. From solution of differential equations it is known that the steady state solution (particular integral) will be of the form

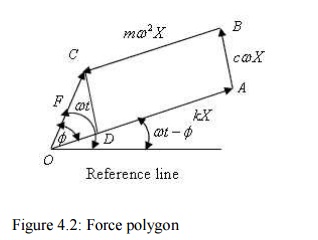
As each term of equation (4.1) represents a forcing term viz., first, second and third terms, represent the inertia force, spring force, and the damping forces. The term in the right hand side of equation (4.1) is the applied force. One may draw a close polygon as shown in figure 4.2 considering the equilibrium of the system under the action of these forces. Considering a reference line these forces can be presented as follows.

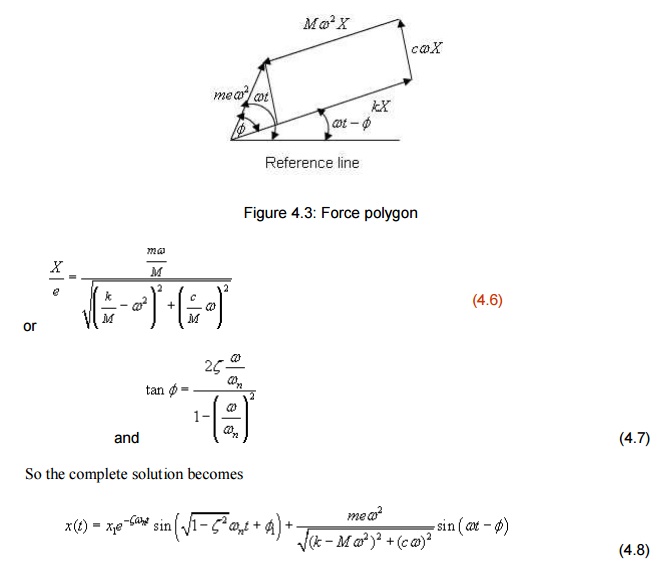
From equation (1), the resultant of the spring force, damping force and the inertia force will be the applied force, which is clearly shown in figure 4.2.

It may be noted that till now, we don't know about the magnitude of X and $  which can be easily computed from Figure 2. Drawing a line CD parallel to AB, from the triangle OCD of Figure 2,

5 FORCED VIBRATION WITH DAMPING:

In this section we will see the behaviour of the spring mass damper model when we add a harmonic force in the form below. A force of this type could, for example, be generated by a rotating imbalance.

If we again sum the forces on the mass we get the following ordinary differential equation:

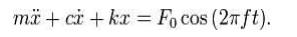
The steady state solution of this problem can be written as:

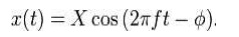
The result states that the mass will oscillate at the same frequency, f, of the applied force, but with a phase shift φ.

The amplitude of the vibration ―X‖ is defined by the following formula.

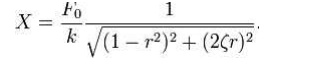
Where ―r‖ is defined as the ratio of the harmonic force frequency over the undamped natural frequency of the mass–spring–damper model.

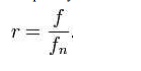
The phase shift , φ, is defined by the following formula.

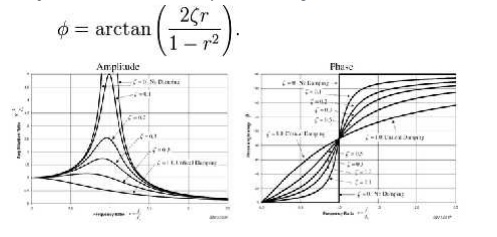
The plot of these functions, called "the frequency response of the system", presents one of the most important features in forced vibration. In a lightly damped system when the forcing frequency nears the natural frequency ( r ~= 1) the amplitude of the vibration can get extremely high. This phenomenon is called resonance (subsequently the natural frequency of a system is often referred to as the resonant frequency). In rotor bearing systems any rotational speed that excites a resonant frequency is referred to as a critical speed.

If  resonance  occurs  in  a  mechanical  system  it  can  be  very  harmful  – leading  to eventual failure of the system. Consequently, one of the major reasons for vibration analysis is to predict when this type of resonance may occur and then to determine what steps to take to prevent it from occurring. As the amplitude plot shows, adding damping can significantly reduce the magnitude of the vibration. Also, the magnitude can be reduced if the natural frequency can be shifted away from the forcing frequency by changing the stiffness or mass of the system. If the  system cannot  be  changed,  perhaps  the  forcing  frequency can  be  shifted  (for  example, changing the speed of the machine generating the force).

The following are some other points in regards to the forced vibration shown in the frequency response plots.

At a given frequency ratio, the amplitude of the vibration, X, is directly proportional to the amplitude of the force F₀ (e.g. if you double the force, the vibration doubles)

With little or no damping, the vibration is in phase with the forcing frequency when the frequency ratio r < 1 and 180 degrees out of phase when the frequency ratio r > 1

by the mass increases with the frequency. Since the deflection seen in the spring, X, is reduced in this region, the force transmitted by the spring (F = kx) to the base is reduced. Therefore the mass–spring–damper≫ system is isolating the harmonic force from the mounting base – referred to as vibration isolation. Interestingly, more damping actually reduces the effects of vibration isolation when r 1 because the damping force (F = cv) is also transmitted to the base.

6 ROTATING UNBALANCE FORCED VIBRATION:

One may find many rotating systems in industrial applications. The unbalanced force in such a system can be represented by a mass m with eccentricity e , which is rotating with angular velocity as shown in Figure 4.1.

Figure 4.1 : Vibrating system with rotating unbalance

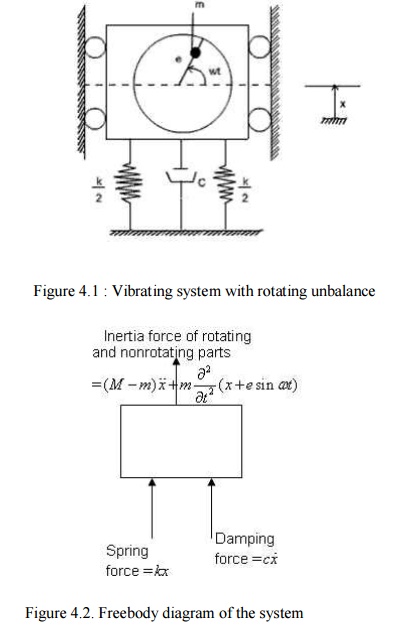
Figure 4.2. Freebody diagram of the system

Let x be the displacement of the nonrotating mass (M-m) from the static equilibrium position, then the displacement of the rotating mass m is  x+esinwt

From the freebody diagram of the system shown in figure 4.2, the equation of motion is

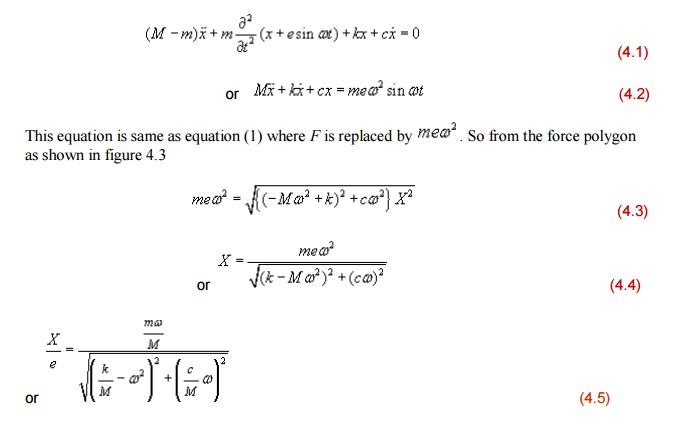
7 VIBRATION ISOLATION AND TRANSMISSIBILITY:

When a machine is operating, it is subjected to several time varying forces because of which it tends to exhibit vibrations. In the process, some of these forces are transmitted to the  foundation – which could undermine the life of the foundation and also affect the operation of any other machine on the same foundation. Hence it is of interest to minimize this force transmission. Similarly when a system is subjected to ground motion, part of the ground motion is transmitted to the system as we just discussed e.g., an automobile going on an uneven road; an instrument mounted on the vibrating surface of an aircraft etc. In these cases, we wish to minimize the motion transmitted from the ground to the system. Such considerations are used in the design of machine foundations and in order to understand some of the basic issues involved, we will study this problem based on the single d.o.f model discussed so far.

we get the expression for force transmitted to the base as follows:

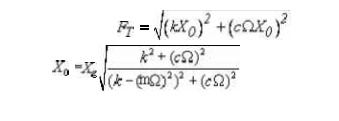
Vibration Isolators:

Consider a vibrating machine; bolted to a rigid floor (Figure 2a).The force transmitted to the floor is equal to the force generated in the machine. The transmitted force can be decreased by adding a suspension and damping elements (often called vibration isolators) Figure 2b , or by adding what is called an inertia block, a large mass (usually a block of cast concrete), directly attached to the machine (Figure 2c).Another option is to add an additional level of mass (sometimes called a seismic mass, again a block of cast concrete) and suspension (Figure 2d).

Figure 2.Vibrat ion iso lat ion systems: a) Machine bo lted to a rigid foundation

b) Supported o n iso lat io n springs, rigid fo u ndat io n c) machine attached to an inertial block. d) Supported on isolation springs, non -rigid foundation (such as a floor); or machine on isolation springs, seismic mass and seco nd level of isolator springs

When oscillatory forces arise unavoidably in machines it is usually desired to prevent these forces from being transmitted to the surroundings. For example, some unbalanced forces are inevitable in a car engine, and it is uncomfortable if these are wholly transmitted to the car body. The usual solution is to mount the source of vibration on sprung supports. Vibration isolation is measured in terms of the motion or force transmitted to the foundation. The lesser the force or motion transmitted the greater the vibration isolation

Suppose that the foundation is effectively rigid and that only one direction of movement is effectively excited so that the system can be treated as having only one degree of freedom.

8 RESPONSE WITHOUT DAMPING:

The amplitude of the force transmitted to the foundations is Where k is the Stiffness of the support and x(t) is the displacement of the mass m.

The governing equation can be determined by considering that the total forcing on the machine is equal to its mass multiplied by its acceleration (Newton’s second law)