Solved Problems: Forced Vibration

SOLVED PROBLEMS

1. Derive the relation for the displacement of mass from the equilibrium position of the damped vibration system with harmonic forcing.

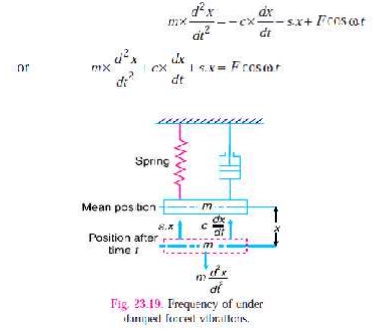
Consider a system consisting of spring, mass and damper as shown in Fig. 23.19. Let the system is acted upon by an external periodic (i.e. simple harmonic) disturbing force,

Fx = F cos ω .t where F = Static force, and

ω       = Angular velocity of the periodic disturbing force.

When the system is constrained to move in vertical guides, it has only one degree of freedom. Let at sometime   t, the mass is displaced downwards through a distance x from its mean position.

The equation of motion may be written as,

This equation of motion may be solved either by differential equation method or by graphi-cal method as discussed below :

1. Differential equation method

The equation (i) is a differential equation of the second degree whose right hand side is some function in t. The solution of such type of differential equation consists of two parts ;

one part is the complementary function and the second is particular integral. Therefore the solution may be written as

x=x₁+x2

where x₁ = Complementary function, and x₂ = Particular integral.

The complementary function is same as discussed in the previous article, i.e.

x₁ = Ce^−at cos (ωd t− θ ) . . .

 (ii) where C and θ are constants. Let us now find the value of particular integral as discussed below :

Let the particular integral of equation (i) is given by

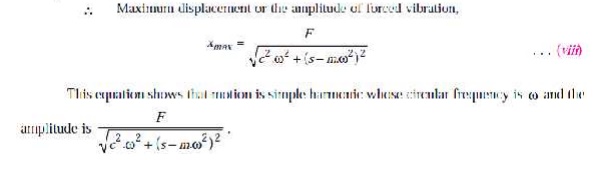
2. A mass of 10 kg is suspended from one end of a helical spring, the other end being fixed. The stiffness of the spring is 10 N/mm. The viscous damping causes the amplitude to decrease to one-tenth of the initial value in four complete oscillations. If a periodic force of 150 cos 50 t N is applied at the mass in the vertical direction, find the amplitude of the forced vibrations. What is its value of resonance ?

3. The mass of an electric motor is 120 kg and it runs at 1500 r.p.m. The armature mass is 35 kg and its C.G. lies 0.5 mm from the axis of rotation. The motor is mounted on five springs of negligible damping so that the force transmitted is one-eleventh of the impressed force. Assume that the mass of the motor is equally distributed among the five springs.

Determine : 1. stiffness of each spring; 2. dynamic force transmitted to the base at the operating speed; and 3. natural frequency of the system.

4. What do you understand by transmissibility? Describe the method of finding the transmissibility ratio from unbalanced machine supported with foundation.

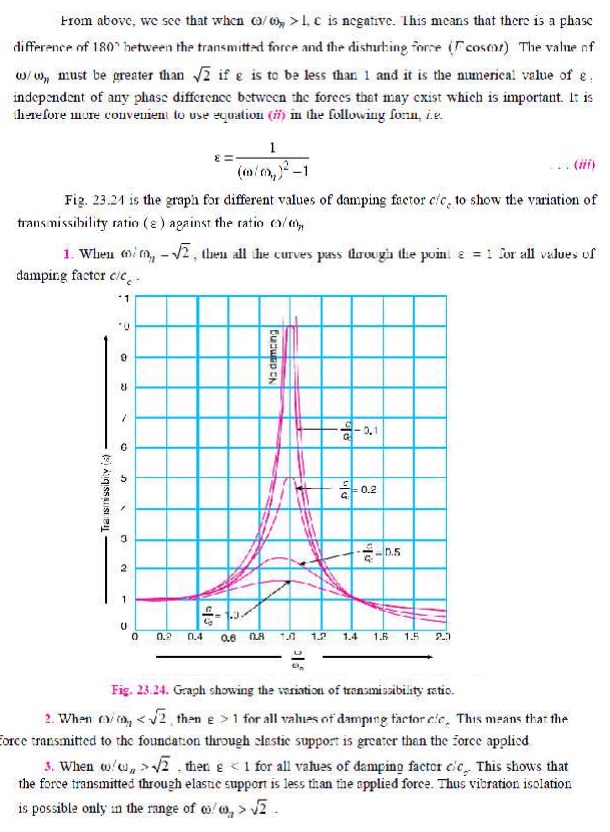
A little consideration will show that when an unbalanced machine is installed on the foundation, it produces vibration in the foundation. In order to prevent these vibrations or to minimize the transmission of forces to the foundation, the machines are mounted on springs and dampers or on some vibration isolating material, as shown in Fig. 23.22. The arrangement is assumed to have one degree of freedom, i.e. it can move up and down only.

It may be noted that when a periodic (i.e. simple harmonic) disturbing force F cos ω t

is applied to a machine of mass m supported by a spring of stiffness s, then the force is transmitted by means of the spring and the damper or dashpot to the fixed support or foundation.

The ratio of the force transmitted (FT) to the force applied (F) is known as the isolation factor or transmissibility ratio of the spring support.

We have discussed above that the force transmitted to the foundation consists of the fol-lowing two forces :

1.             Spring force or elastic force which is equal to s. xmax, and

2.             Damping force which is equal to c. ω .xmax.

Since these two forces are perpendicular to one another, as shown in Fig.23.23, therefore the force transmitted,

5. A machine has a mass of 100 kg and unbalanced reciprocating parts of mass 2 kg which move through a vertical stroke of 80 mm with simple harmonic motion. The machine is mounted on four springs, symmetrically arranged with respect to centre of mass, in such a way that the machine has one degree of freedom and can undergo vertical displacements only.

Neglecting damping, calculate the combined stiffness of the spring in order that the force transmitted to the foundation is 1 / 25 th of the applied force, when the speed of rotation of ma-chine crank shaft is 1000 r.p.m.

When the machine is actually supported on the springs, it is found that the damping reduces the amplitude of successive free vibrations by 25%. Find : 1. the force transmitted to foundation at 1000 r.p.m., 2. the force transmitted to the foundation at resonance, and 3. the amplitude of the forced vibration of the machine at resonance.

6.(i) Derive the relation for magnification factor in case of forced vibration.

6.(ii) A single cylinder vertical petrol engine of total mass 300 kg is mounted upon a steel chassis frame and causes a vertical static deflection of 2 mm. The reciprocating parts of the engine has a mass of 20 kg and move through a vertical stroke of 150 mm with simple harmonic motion. A dashpot is provided whose damping resistance is directly proportional to the velocity and amounts to 1.5 kN per metre per second.

Considering that the steady state of vibration is reached ; determine : 1. the amplitude of forced vibrations, when the driving shaft of the engine rotates at 480 r.p.m., and 2. the speed of the driving shaft at which resonance will occur.

Solution : Given. m = 300 kg; δ = 2 mm = 2 × 10^–3       m ; m1 = 20 kg ; l = 150 mm

= 0.15 m ; c = 1.5 kN/m/s = 1500 N/m/s ; N = 480 r.p.m. or ω = 50.3 rad/s

 TUTORIAL PROBLEMS:

1.             A machine of mass 100 kg is supported on openings of total stiffness 800 kN/m and has a rotating unbalanced element which results in a disturbing force of 400 N at a speed of 3000 r.p.m. Assum-ing the damping ratio as 0.25, determine : 1. the amplitude of vibrations due to unbalance ; and 2. the transmitted force. [Ans. 0.04mm

; 35.2 N]

2.             A mass of 500 kg is mounted on supports having a total stiffness of 100 kN/m and which provides viscous damping, the damping ratio being 0.4. The mass is constrained to move vertically and is subjected to a vertical disturbing force of the

type F cos ω t. Determine the frequency at which resonance will occur and the maximum allowable value of F if the amplitude at resonance is to be restricted to 5mm

[Ans. 2.25 Hz ; 400 N]

3.            A machine of mass 75 kg is mounted on springs of stiffness 1200 kN/m and with an assumed damping factor of 0.2. A piston within the machine of mass 2 kg has a reciprocating motion with a stroke of 80 mm and a speed of 3000 cycles/min. Assuming the motion to be simple harmonic, find : 1. the amplitude of motion of the machine, 2. its phase angle with respect to the exciting force, 3. the force transmitted to the foundation, and 4. the phase angle of transmitted force with respect to the exciting force. [Ans. 1.254 mm ; 169.05° ; 2132 N ; 44.8°]