Chapter: Cryptography and Network Security Principles and Practice : Cryptographic Data Integrity Algorithms : Digital Signatures
Schnorr Digital Signature Scheme
SCHNORR DIGITAL SIGNATURE SCHEME
As with the ElGamal digital signature scheme, the Schnorr signature scheme is based
on discrete logarithms . The Schnorr scheme minimizes the message-dependent
amount of computation required to generate a signature. The main work for signature generation does not depend
on the message and can be done during the idle time of the processor. The message-dependent part of the signature generation requires multiplying a
2n-bit
integer with an n-bit integer.
The scheme is based on using a prime modulus p, with p - 1 having a prime factor q of appropriate size; that is,
p - 1 == (mod q). Typically, we
use p ~~ 21024 and q ~ 2160. Thus, p is a 1024-bit
number, and q is a 160-bit
number, which is also
the length of the SHA-1
hash value.
The first part of this scheme is the
generation of a private/public key pair, which consists of the following steps.
1.
Choose primes
p
and q, such that q is a prime factor
of p - 1.
2.
Choose an integer
a, such that aq = 1 mod p. The values a, p, and q comprise a global public key that can be common
to a group of users.
3.
Choose a random
integer s with 0 < s < q. This is the user’s private
key.
4.
Calculate v = a - s mod
p. This is the user’s public key.
A user with private key s and
public key v generates a
signature as follows.
1.
Choose a random
integer r with 0 < r < q and compute x = armod p. This computation is a preprocessing stage independent of the message M to be signed.
2.
Concatenate the message
with x and hash the result to compute
the value e:
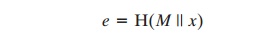
3.
Compute y = (r + se) mod q. The signature
consists of the pair (e, y).
Any other user can verify the signature as
follows.
1.
Compute x' = ayve mod p.
2.
Verify that e = H(M || x').
To see that the verification works, observe
that
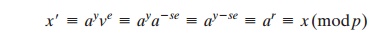
Hence,
H(M
|| x') = H(M
|| x).
Related Topics