Digital Signatures: Properties, Attacks and Forgeries

DIGITAL SIGNATURES

Properties

Message authentication protects two parties who exchange messages from any third party. However, it does not protect the two parties against each other. Several forms of dispute between the two are possible.

For example, suppose that John sends an authenticated message to Mary, using one of the schemes of Figure 12.1. Consider the following disputes that could arise.

1.                        Mary may forge a different message and claim that it came from John. Mary would simply have to create a message and append an authentication code using the key that John and Mary share.

2.                        John can deny sending the message. Because it is possible for Mary to forge a message, there is no way to prove that John did in fact send the message.

Both scenarios are of legitimate concern. Here is an example of the first sce- nario: An electronic funds transfer takes place, and the receiver increases the amount of funds transferred and claims that the larger amount had arrived from the sender. An example of the second scenario is that an electronic mail message contains instructions to a stockbroker for a transaction that subsequently turns out badly. The sender pretends that the message was never sent.

In situations where there is not complete trust between sender and receiver, something more than authentication is needed. The most attractive solution to this problem is the digital signature. The digital signature must have the following properties:

•                           It must verify the author and the date and time of the signature.

•                           It must authenticate the contents at the time of the signature.

•                           It must be verifiable by third parties, to resolve disputes.

Thus, the digital signature function includes the authentication function.

Attacks and Forgeries

[GOLD88] lists the following types of attacks, in order of increasing severity. Here A denotes the user whose signature method is being attacked, and C denotes the attacker.

•                 Key-only attack: C only knows A’s public key.

•                 Known message attack: C is given access to a set of messages and their signatures.

•                 Generic chosen message attack: C chooses a list of messages before attempt- ing to breaks A’s signature scheme, independent of A’s public key. C then obtains from A valid signatures for the chosen messages. The attack is generic, because it does not depend on A’s public key; the same attack is used against everyone.

•                 Directed chosen message attack: Similar to the generic attack, except that the list of messages to be signed is chosen after C knows A’s public key but before any signatures are seen.

•                 Adaptive chosen message attack: C is allowed to use A as an “oracle.” This means the A may request signatures of messages that depend on previously obtained message–signature pairs.

[GOLD88] then defines success at breaking a signature scheme as an outcome in which C can do any of the following with a non-negligible probability:

•                 Total break: C determines A’s private key.

•                 Universal forgery: C finds an efficient signing algorithm that provides an equivalent way of constructing signatures on arbitrary messages.

•                 Selective forgery: C forges a signature for a particular message chosen by C.

•                 Existential forgery: C forges a signature for at least one message. C has no control over the message. Consequently, this forgery may only be a minor nuisance to A.

Digital Signature Requirements

On the basis of the properties and attacks just discussed, we can formulate the fol- lowing requirements for a digital signature.

•                 The signature must be a bit pattern that depends on the message being signed.

•                 The signature must use some information unique to the sender to prevent both forgery and denial.

•                 It must be relatively easy to produce the digital signature.

•                 It must be relatively easy to recognize and verify the digital signature.

•                 It must be computationally infeasible to forge a digital signature, either by constructing a new message for an existing digital signature or by constructing a fraudulent digital signature for a given message.

•                 It must be practical to retain a copy of the digital signature in storage.

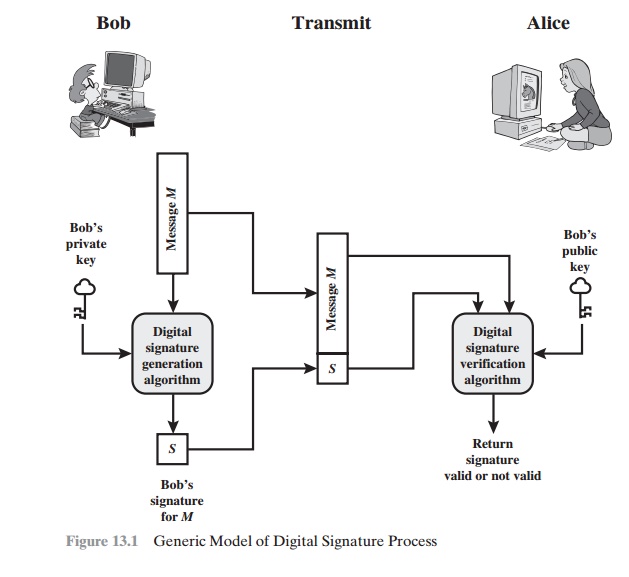
A secure hash function, embedded in a scheme such as that of Figure 13.2, provides a basis for satisfying these requirements. However, care must be taken in the design of the details of the scheme.

Direct Digital Signature

The term direct digital signature refers to a digital signature scheme that involves only the communicating parties (source, destination). It is assumed that the destina- tion knows the public key of the source.

Confidentiality can be provided by encrypting the entire message plus signa- ture with a shared secret key (symmetric encryption). Note that it is important to perform the signature function first and then an outer confidentiality function. In case of dispute, some third party must view the message and its signature. If the signature is calculated on an encrypted message, then the third party also needs access to the decryption key to read the original message. However, if the signature is the inner operation, then the recipient can store the plaintext message and its sig- nature for later use in dispute resolution.

The validity of the scheme just described depends on the security of the sender’s private key. If a sender later wishes to deny sending a particular message, the sender can claim that the private key was lost or stolen and that someone else forged his or her signature. Administrative controls relating to the security of pri- vate keys can be employed to thwart or at least weaken this ploy, but the threat is still there, at least to some degree. One example is to require every signed message to include a timestamp (date and time) and to require prompt reporting of compro- mised keys to a central authority.

Another threat is that some private key might actually be stolen from X at time T. The opponent can then send a message signed with X’s signature and stamped with a time before or equal to T.

The universally accepted technique for dealing with these threats is the use of  a  digital certificate and  certificate authorities. We  defer a  discussion  of this topic until Chapter 14, and focus in this chapter on digital signature algorithms.