ELGAMAL Digital Signature Scheme

ELGAMAL DIGITAL SIGNATURE SCHEME

Before examining the NIST Digital Signature standard, it will be helpful to under- stand the ElGamal and Schnorr signature schemes. Recall from Chapter 10, that the ElGamal encryption scheme is designed to enable encryption by a user’s public key with decryption by the user’s private key. The ElGamal signature scheme involves the use of the private key for encryption and the public key for decryption [ELGA84, ELGA85].

Before proceeding, we need a result from number theory. Recall from Chapter 8 that for a prime number q, if a is a primitive root of q, then

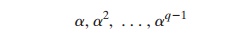
are distinct (mod q). It can be shown that, if a is a primitive root of q, then

As with ElGamal encryption, the global elements of ElGamal digital signature are a prime number q and a, which is a primitive root of q. User A generates a private/public key pair as follows.

1.                        Generate a random integer XA, such that 1 6 XA<q - 1.

2.                        Compute YA  =  aXA mod q.

3.                        A’s private key is XA; A’s pubic key is {q, a, YA}.

To sign a message M, user A first computes the hash m = H(M), such that m is an integer in the range 0 <= m <= q - 1. A then forms a digital signature as follows.

1.                        Choose a random integer K such that 1 <= K <= q - 1 and gcd(K, q - 1) = 1. That is, K is relatively prime to q - 1.

2.                        Compute S1 = aKmod q. Note that this is the same as the computation of C1

for ElGamal encryption.

3.                        Compute K- 1mod (q - 1). That is, compute the inverse of K modulo q - 1.

4.                        Compute S2 = K- 1(m - XAS1) mod (q - 1).

5.                        The signature consists of the pair (S1, S2). Any user B can verify the signature as follows.

1.                        Compute V1  =  am mod q.

2.                       

The signature is valid if V1 = V2. Let us demonstrate that this is so. Assume that the equality is true. Then we have

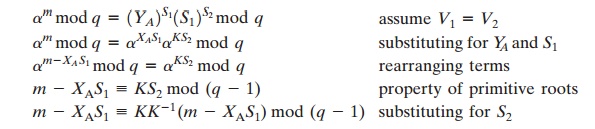
For example, let us start with the prime field GF(19); that is, q = 19. It has primitive roots {2, 3, 10, 13, 14, 15}, as shown in Table 8.3. We choose a = 10.

Alice generates a key pair as follows:

1.                        Alice chooses XA = 16.

2.                        Then YA  =  aXA mod q  =  a16 mod 19  =  4.

3.                        Alice’s private key is 16; Alice’s pubic key is {q, a, YA}  =  {19, 10, 4}. Suppose Alice wants to sign a message with hash value m  =  14.

1.                        Alice chooses K = 5, which is relatively prime to q - 1 = 18.

2.                        S1  = aKmod q  = 105mod 19  = 3 (see Table  8.3).