Digital Signature Standard

DIGITAL SIGNATURE STANDARD

The National Institute of Standards and Technology (NIST) has published Federal Information Processing Standard FIPS 186, known as the Digital Signature Standard (DSS). The DSS makes use of the Secure Hash Algorithm (SHA) described in Chapter 12 and presents a new digital signature technique, the Digital Signature Algorithm (DSA). The DSS was originally proposed in 1991 and revised in 1993 in response to public feedback concerning the security of the scheme. There was a further minor revision in 1996. In 2000, an expanded version of the standard was issued as FIPS 186-2, subsequently updated to FIPS 186-3 in 2009. This latest version also incorporates digital signature algorithms based on RSA and on elliptic curve cryptography. In this section, we discuss the original DSS algorithm.

The DSS Approach

The DSS uses an algorithm that is designed to provide only the digital signature function. Unlike RSA, it cannot be used for encryption or key exchange. Nevertheless, it is a public-key technique.

Figure 13.3 contrasts the DSS approach for generating digital signatures to that used with RSA. In the RSA approach, the message to be signed is input to a hash function that produces a secure hash code of fixed length. This hash code is then encrypted using the sender’s private key to form the signature. Both the mes- sage and the signature are then transmitted. The recipient takes the message and produces a hash code. The recipient also decrypts the signature using the sender’s public key. If the calculated hash code matches the decrypted signature, the signa- ture is accepted as valid. Because only the sender knows the private key, only the sender could have produced a valid signature.

The DSS approach also makes use of a hash function. The hash code is pro- vided as input to a signature function along with a random number k generated for this particular signature. The signature function also depends on the sender’s private key (PRa) and a set of parameters known to a group of communicating principals.

We can consider this set to constitute a global public key (PUG).1 The result is a signature consisting of two components, labeled s and r.

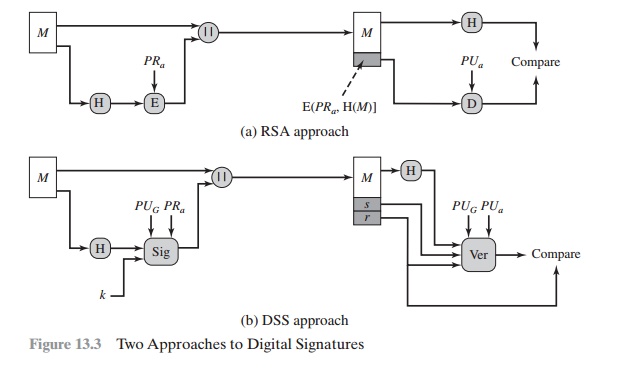
At the receiving end, the hash code of the incoming message is generated. This plus the signature is input to a verification function. The verification function also depends on the global public key as well as the sender’s public key (PUa), which is paired with the sender’s private key. The output of the verification function is a value that is equal to the signature component r if the signature is valid. The signa- ture function is such that only the sender, with knowledge of the private key, could have produced the valid signature.

We turn now to the details of the algorithm.

The Digital Signature Algorithm

The DSA is based on the difficulty of computing discrete logarithms (see Chapter 8) and is based on schemes originally presented by ElGamal [ELGA85] and Schnorr [SCHN91].

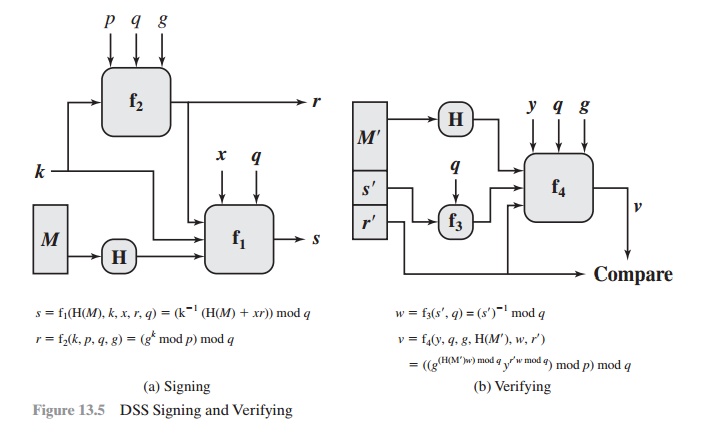
Figure 13.4 summarizes the algorithm. There are three parameters that are pub- lic and can be common to a group of users. A 160-bit prime number q is chosen. Next, a prime number p is selected with a length between 512 and 1024 bits such that q

divides (p - 1). Finally, g is chosen to be of the form h(p - 1)/q mod p, where h is an

integer between 1 and (p - 1) with the restriction that g must be greater than 1.2 Thus, the global public-key components of DSA have the same for as in the Schnorr signature scheme.

With these numbers in hand, each user selects a private key and generates a public key. The private key x must be a number from 1 to (q - 1) and should be cho- sen randomly or pseudorandomly. The public key is calculated from the private key as y = gx mod p. The calculation of y given x is relatively straightforward. However, given the public key y, it is believed to be computationally infeasible to determine x, which is the discrete logarithm of y to the base g, modp (see Chapter 8).

To create a signature, a user calculates two quantities, r and s, that are func- tions of the public key components (p, q, g), the user’s private key (x), the hash code of the message H(M), and an additional integer k that should be generated randomly or pseudorandomly and be unique for each signing.

At the receiving end, verification is performed using the formulas shown in Figure 13.4.The receiver generates a quantity v that is a function of the public key com- ponents, the sender’s public key, and the hash code of the incoming message. If this quantity matches the r component of the signature, then the signature is validated.

Figure 13.5 depicts the functions of signing and verifying.

The structure of the algorithm, as revealed in Figure 13.5, is quite interesting. Note that the test at the end is on the value r, which does not depend on the message at all. Instead, r is a function of k and the three global public-key components. The multiplicative inverse of k (mod q) is passed to a function that also has as inputs the message hash code and the user’s private key. The structure of this function is such that the receiver can recover r using the incoming message and signature, the public key of the user, and the global public key. It is certainly not obvious from Figure 13.4 or Figure 13.5 that such a scheme would work. A proof is provided in Appendix K. Given the difficulty of taking discrete logarithms, it is infeasible for an oppo-

nent to recover k from r or to recover x from s.

Another point worth noting is that the only computationally demanding task in signature generation is the exponential calculation gk mod p. Because this value does not depend on the message to be signed, it can be computed ahead of time.

Indeed, a user could precalculate a number of values of r to be used to sign documents as needed. The only other somewhat demanding task is the determina- tion of a multiplicative inverse, k- 1. Again, a number of these values can be precalculated.