Chapter: Control Systems : Time Response Analysis
Root Locus Technique, Analysis and Application Procedure
Root Locus Technique
o Introduced by W. R. Evans in 1948
o Graphical method, in which movement of poles in the s-plane is sketched when some parameter is varied The path taken by the roots of the characteristic equation when open loop gain K is varied from 0 to ∞ are called root loci
o Direct Root Locus = 0 < k < ∞
o Inverse Root Locus = - ∞ < k < 0
Root Locus Analysis:
o The roots of the closed-loop characteristic equation define the system characteristic responses
o Their location in the complex s-plane lead to prediction of the characteristics of the time domain responses in terms of:
o damping ratio ζ,
o natural frequency, wn
o damping constant ζ, first-order modes
o Consider how these roots change as the loop gain is varied from 0 to∞
Basics of Root Locus:
o Symmetrical about real axis
o RL branch starts from OL poles and terminates at OL zeroes
o No. of RL branches = No. of poles of OLTF
o Centroid is common intersection point of all the asymptotes on the real axis
o Asymptotes are straight lines which are parallel to RL going to ∞ and meet the RL at ∞
o No. of asymptotes = No. of branches going to ∞
o At Break Away point , the RL breaks from real axis to enter into the complex plane
o At BI point, the RL enters the real axis from the complex plane
Constructing Root Locus:
o Locate the OL poles & zeros in the plot Find the branches on the real axis
o Find angle of asymptotes & centroid
o Φa= ±180º(2q+1) / (n-m)
o ζa = (Σpoles - Σzeroes) / (n-m) Find BA and BI points
o Find Angle Of departure (AOD) and Angle Of Arrival (AOA)
o AOD = 180º- (sum of angles of vectors to the complex pole from all other poles) + (Sum of angles of vectors to the complex pole from all zero)
o AOA = 180º- (sum of angles of vectors to the complex zero from all other zeros) + (sum of angles of vectors to the complex zero from poles)
o Find the point of intersection of RL with the imaginary axis.
Application of the Root Locus Procedure
Step 1: Write the characteristic equation as
1+ F(s)= 0
Step 2: Rewrite preceding equation into the form of poles and zeros as follows
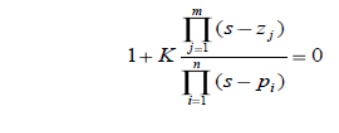
Step 3:
Locate the poles and zeros with specific symbols, the root locus begins at the open-loop poles and ends at the open loop zeros as K increases from 0 to infinity
If open-loop system has n-m zeros at infinity, there will be n-m branches of the root locus approaching the n-m zeros at infinity
Step 4:
The root locus on the real axis lies in a section of the real axis to the left of an odd number of real poles and zeros
Step 5:
The number of separate loci is equal to the number of open-loop poles
Step 6:
The root loci must be continuous and symmetrical with respect to the horizontal real axis
Step 7:
The loci proceed to zeros at infinity along asymptotes centered at centroid and with angles
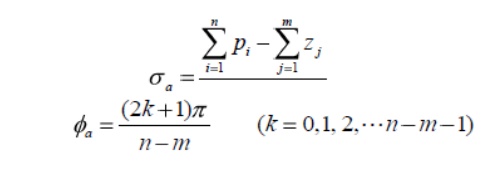
Step 8:
The actual point at which the root locus crosses the imaginary axis is readily evaluated by using Routh‗s criterion
Step 9:
Determine the breakaway point d (usually on the real axis)
Step 10:
Plot the root locus that satisfy the phase criterion
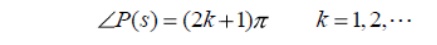
Step 11:
Determine the parameter value K1 at a specific root using the magnitude criterion
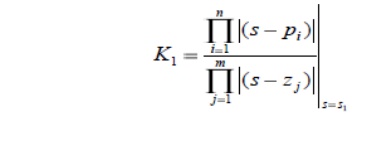
Related Topics