Retrieval Models

Retrieval Models

In this section we briefly describe the important models of IR. These are the three main statistical models—Boolean, vector space, and probabilistic—and the semantic model.

1. Boolean Model

In this model, documents are represented as a set of terms. Queries are formulated as a combination of terms using the standard Boolean logic set-theoretic operators such as AND, OR and NOT. Retrieval and relevance are considered as binary concepts in this model, so the retrieved elements are an “exact match” retrieval of relevant documents. There is no notion of ranking of resulting documents. All retrieved documents are considered equally important—a major simplification that does not consider frequencies of document terms or their proximity to other terms com-pared against the query terms.

Boolean retrieval models lack sophisticated ranking algorithms and are among the earliest and simplest information retrieval models. These models make it easy to associate metadata information and write queries that match the contents of the documents as well as other properties of documents, such as date of creation, author, and type of document.

2. Vector Space Model

The vector space model provides a framework in which term weighting, ranking of retrieved documents, and relevance feedback are possible. Documents are represented as features and weights of term features in an n-dimensional vector space of terms. Features are a subset of the terms in a set of documents that are deemed most relevant to an IR search for this particular set of documents. The process of selecting these important terms (features) and their properties as a sparse (limited) list out of the very large number of available terms (the vocabulary can contain hundreds of thousands of terms) is independent of the model specification. The query is also specified as a terms vector (vector of features), and this is compared to the document vectors for similarity/relevance assessment.

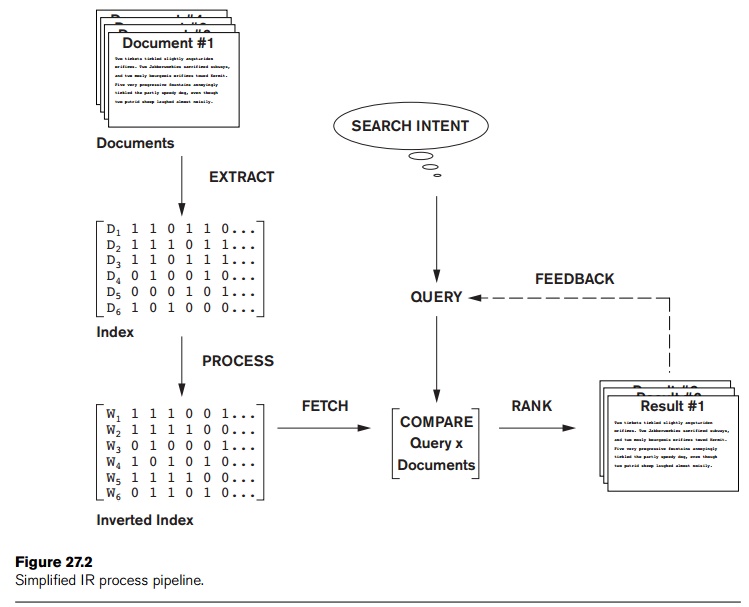
The similarity assessment function that compares two vectors is not inherent to the model—different similarity functions can be used. However, the cosine of the angle between the query and document vector is a commonly used function for similarity assessment. As the angle between the vectors decreases, the cosine of the angle approaches one, meaning that the similarity of the query with a document vector increases. Terms (features) are weighted proportional to their frequency counts to reflect the importance of terms in the calculation of relevance measure. This is different from the Boolean model, which does not take into account the frequency of words in the document for relevance match.

In the vector model, the document term weight w_ij (for term i in document j) is represented based on some variation of the TF (term frequency) or TF-IDF (term frequency-inverse document frequency) scheme (as we will describe below). TF-IDF is a statistical weight measure that is used to evaluate the importance of a document word in a collection of documents. The following formula is typically used:

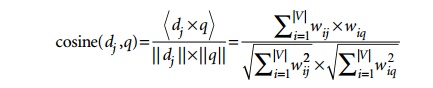
In the formula given above, we use the following symbols:

        d_j is the document vector.

        q is the query vector.

        w_ij is the weight of term i in document j.

        w_iq is the weight of term i in query vector q.

|V| is the number of dimensions in the vector that is the total number of important keywords (or features).

 TF-IDF uses the product of normalized frequency of a term i (TF_ij) in document D_j and the inverse document frequency of the term i (IDF_i) to weight a term in a document. The idea is that terms that capture the essence of a document occur fre-quently in the document (that is, their TF is high), but if such a term were to be a good term that discriminates the document from others, it must occur in only a few documents in the general population (that is, its IDF should be high as well).

IDF values can be easily computed for a fixed collection of documents. In case of Web search engines, taking a representative sample of documents approximates IDF computation. The following formulas can be used:

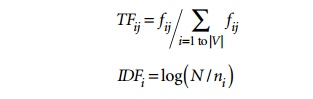
In these formulas, the meaning of the symbols is:

        TF_ij is the normalized term frequency of term i in document D_j.

        f_ij is the number of occurrences of term i in document D_j.

        IDF_i is the inverse document frequency weight for term i.

        N is the number of documents in the collection.

        n_i is the number of documents in which term i occurs.

Note that if a term i occurs in all documents, then n_i = N and hence IDF_i = log (1) becomes zero, nullifying its importance and creating a situation where division by zero can occur. The weight of term i in document j, w_ij is computed based on its TF-IDF value in some techniques. To prevent division by zero, it is common to add a 1 to the denominator in the formulae such as the cosine formula above.

Sometimes, the relevance of the document with respect to a query (rel(D_j,Q)) is directly measured as the sum of the TF-IDF values of the terms in the Query Q:

The normalization factor (similar to the denominator of the cosine formula) is incorporated into the TF-IDF formula itself, thereby measuring relevance of a document to the query by the computation of the dot product of the query and document vectors.

The Rocchio algorithm is a well-known relevance feedback algorithm based on the vector space model that modifies the initial query vector and its weights in response to user-identified relevant documents. It expands the original query vector q to a new vector q_e as follows:

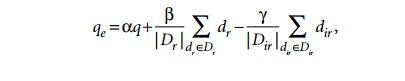
Here, D_r and D_ir are relevant and nonrelevant document sets and α, β, and γ are parameters of the equation. The values of these parameters determine how the feed-back affects the original query, and these may be determined after a number of trial-and-error experiments.

3. Probabilistic Model

The similarity measures in the vector space model are somewhat ad hoc. For example, the model assumes that those documents closer to the query in cosine space are more relevant to the query vector. In the probabilistic model, a more concrete and definitive approach is taken: ranking documents by their estimated probability of relevance with respect to the query and the document. This is the basis of the Probability Ranking Principle developed by Robertson:

In the probabilistic framework, the IR system has to decide whether the documents belong to the relevant set or the nonrelevant set for a query. To make this decision, it is assumed that a predefined relevant set and nonrelevant set exist for the query, and the task is to calculate the probability that the document belongs to the relevant set and compare that with the probability that the document belongs to the nonrelevant set.

Given the document representation D of a document, estimating the relevance R and nonrelevance NR of that document involves computation of conditional prob-ability P(R|D) and P(NR|D). These conditional probabilities can be calculated using Bayes’ Rule:

P(R|D) = P(D|R) × P(R)/P(D)

P(NR|D) = P(D|NR) × P(NR)/P(D)

A document D is classified as relevant if P(R|D) > P(NR|D). Discarding the constant P(D), this is equivalent to saying that a document is relevant if:

P(D|R) × P(R) > P(D|NR) × P(NR)

The likelihood ratio P(D|R)/P(D|NR) is used as a score to determine the likelihood of the document with representation D belonging to the relevant set.

The term independence or Naïve Bayes assumption is used to estimate P(D|R) using computation of P(t_i|R) for term t_i. The likelihood ratios P(D|R)/P(D|NR) of documents are used as a proxy for ranking based on the assumption that highly ranked documents will have a high likelihood of belonging to the relevant set.

With some reasonable assumptions and estimates about the probabilistic model along with extensions for incorporating query term weights and document term weights in the model, a probabilistic ranking algorithm called BM25 (Best Match 25) is quite popular. This weighting scheme has evolved from several versions of the Okapi system.

The Okapi weight for Document d_j and query q is computed by the formula below. Additional notations are as follows:

t_i is a term.

f_ij is the raw frequency count of term t_i in document d_j.

f_iq is the raw frequency count of term t_i in query q.

N is the total number of documents in the collection.

df_i is the number of documents that contain the term t_i.

dl_j is the document length (in bytes) of d_j.

avdl is the average document length of the collection.

The Okapi relevance score of a document d_j for a query q is given by the equation below, where k₁ (between 1.0–2.0), b (usually 0.75) ,and k₂ (between 1–1000) are parameters:

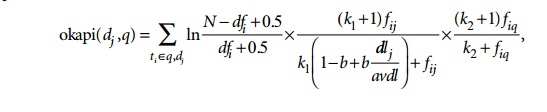
4. Semantic Model

However sophisticated the above statistical models become, they can miss many relevant documents because those models do not capture the complete meaning or information need conveyed by a user’s query. In semantic models, the process of matching documents to a given query is based on concept level and semantic matching instead of index term (keyword) matching. This allows retrieval of relevant documents that share meaningful associations with other documents in the query result, even when these associations are not inherently observed or statistically captured.

Semantic approaches include different levels of analysis, such as morphological, syntactic, and semantic analysis, to retrieve documents more effectively. In morphological analysis, roots and affixes are analyzed to determine the parts of speech (nouns, verbs, adjectives, and so on) of the words. Following morphological analysis, syntactic analysis follows to parse and analyze complete phrases in docu-ments. Finally, the semantic methods have to resolve word ambiguities and/or generate relevant synonyms based on the semantic relationships between levels of structural entities in documents (words, paragraphs, pages, or entire documents).

The development of a sophisticated semantic system requires complex knowledge bases of semantic information as well as retrieval heuristics. These systems often require techniques from artificial intelligence and expert systems. Knowledge bases like Cyc and WordNet have been developed for use in knowledge-based IR systems based on semantic models. The Cyc knowledge base, for example, is a represen-tation of a vast quantity of commonsense knowledge about assertions (over 2.5 million facts and rules) interrelating more than 155,000 concepts for reasoning about the objects and events of everyday life. WordNet is an extensive thesaurus (over 115,000 concepts) that is very popular and is used by many systems and is under continuous development (see Section 27.4.3).