Resistance to Blood Flow

Resistance to Blood Flow

Units of Resistance. Resistance is the impediment toblood flow in a vessel, but it cannot be measured by any direct means. Instead, resistance must be calcu-lated from measurements of blood flow and pressure difference between two points in the vessel. If the pressure difference between two points is 1 mm Hg and the flow is 1 ml/sec, the resistance is said to be 1 peripheral resistance unit, usually abbreviated PRU.

        Expression of Resistance in CGS Units. Occasionally, abasic physical unit called the CGS (centimeters, grams, seconds) unit is used to express resistance. This unit is dyne seconds/centimeters5. Resistance in these units can be calculated by the following formula

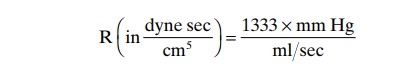
Total Peripheral Vascular Resistance and Total Pulmonary Vas-cular Resistance. The rate of bloodflow through theentire circulatory system is equal to the rate of blood pumping by the heart—that is, it is equal to the cardiac output. In the adult human being, this is approximately 100 ml/sec. The pressure difference from the systemic arteries to the systemic veins is about 100 mm Hg. Therefore, the resistance of the entire systemic circu-lation, called the total peripheral resistance, is about 100/100, or 1 PRU.

In conditions in which all the blood vessels through-out the body become strongly constricted, the total peripheral resistance occasionally rises to as high as 4 PRU. Conversely, when the vessels become greatly dilated, the resistance can fall to as little as 0.2 PRU.

In the pulmonary system, the mean pulmonary arte-rial pressure averages 16 mm Hg and the mean left atrial pressure averages 2 mm Hg, giving a net pres-sure difference of 14 mm. Therefore, when the cardiac output is normal at about 100 ml/sec, the totalpulmonary vascular resistance calculates to be about0.14 PRU (about one seventh that in the systemic circulation).

“Conductance” of Blood in a Vessel and Its Relation to Resis- tance. Conductance is a measure of the bloodflowthrough a vessel for a given pressure difference. This is generally expressed in terms of milliliters per second per millimeter of mercury pressure, but it can also be expressed in terms of liters per second per millimeter of mercury or in any other units of blood flow and pressure.

It is evident that conductance is the exact reciprocal of resistance in accord with the following equation:

Very Slight Changes in Diameter of a Vessel Can Change Its Conductance Tremendously! Slight changes in the diame-ter of a vessel cause tremendous changes in the vessel’s ability to conduct blood when the blood flow is stream-lined. This is demonstrated by the experiment illus-trated in Figure 14–9A, which shows three vessels with relative diameters of 1, 2, and 4 but with the same pres-sure difference of 100 mm Hg between the two ends of the vessels. Although the diameters of these vessels

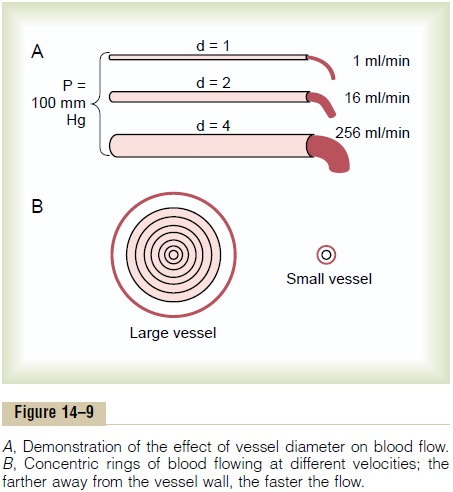
increase only fourfold, the respective flows are 1, 16, and 256 ml/mm, which is a 256-fold increase in flow. Thus, the conductance of the vessel increases in pro-portion to the fourth power of the diameter, in accor-dance with the following formula:

Poiseuille’s Law. The cause of this great increase in conductance when the diameter increases can be explained by referring to Figure 14–9B, which shows cross sections of a large and a small vessel. The concentric rings inside the vessels indicate that the velocity of flow in each ring is different from that in the adjacent rings because of laminar flow, which was discussed earlier.That is, the blood in the ring touching the wall of the vessel is barely flowing because of its adherence to the vascular endothelium. The next ring of blood toward the center of the vessel slips past the first ring and, therefore, flows more rapidly. The third, fourth, fifth, and sixth rings likewise flow at progressively increasing velocities. Thus, the blood that is near the wall of the vessel flows extremely slowly, whereas that in the middle of the vessel flows extremely rapidly.

In the small vessel, essentially all the blood is near the wall, so that the extremely rapidly flowing central stream of blood simply does not exist. By integrating the velocities of all the concentric rings of flowing blood and multiplying them by the areas of the rings, one can derive the following formula, known as Poiseuille’s law

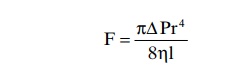
in which F is the rate of blood flow, DP is the pressure difference between the ends of the vessel, r is the radius of the vessel, l is length of the vessel, and h is viscosity of the blood.

Note particularly in this equation that the rate of blood flow is directly proportional to the fourth powerof the radius of the vessel, which demonstrates onceagain that the diameter of a blood vessel (which is equal to twice the radius) plays by far the greatest role of all factors in determining the rate of blood flow through a vessel.

Importance of the Vessel Diameter “Fourth Power Law” in Determining Arteriolar Resistance. In the systemic circula-tion, about two thirds of the total systemic resistance to blood flow is arteriolar resistance in the small arterioles. The internal diameters of the arterioles range from as little as 4 micrometers to as great as 25 micrometers. However, their strong vascular walls allow the internal diameters to change tremendously, often as much as fourfold. From the fourth power law discussed above that relates blood flow to diameter of the vessel, one can see that a fourfold increase in vessel diameter can increase the flow as much as 256-fold. Thus, this fourth power law makes it possible for the arterioles, responding with only small changes in diameter to nervous signals or local tissue chemical signals, either to turn off almost completely the blood flow to the tissue or at the other extreme to cause a vast increase in flow. Indeed, ranges of blood flow of more than 100-fold in separate tissue areas have been recorded between the limits of maximum arteriolar constriction and maximum arteriolar dilatation.

Resistance to Blood Flow in Series and Parallel Vascular Cir- cuits. Blood pumped by the heartflows from the highpressure part of the systemic circulation (i.e., aorta) to the low pressure side (i.e., vena cava) through many miles of blood vessels arranged in series and in paral-lel. The arteries, arterioles, capillaries, venules, and veins are collectively arranged in series. When blood vessels are arranged in series, flow through each blood vessel is the same and the total resistance to blood flow (Rtotal) is equal to the sum of the resistances of each vessel:

R total  = R1 + R 2 + R3 + R4 . . .

The total peripheral vascular resistance is therefore equal to the sum of resistances of the arteries, arteri-oles, capillaries, venules, and veins. In the example shown in Figure 14–10A, the total vascular resistance is equal to the sum of R1 and R2.

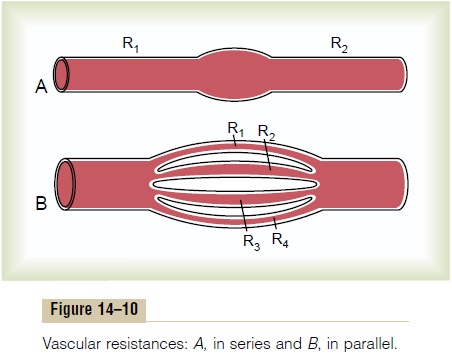
Blood vessels branch extensively to form parallel circuits that supply blood to the many organs and tissues of the body. This parallel arrangement permits each tissue to regulate its own blood flow, to a great extent, independently of flow to other tissues.

For blood vessels arranged in  parallel      (Figure 14–10B), the total resistance to blood flow is expressed as:

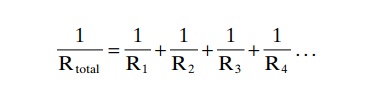
It is obvious that for a given pressure gradient, far greater amounts of blood will flow through this parallel system than through any of the individual blood vessels. Therefore, the total resistance is far less than the resistance of any single blood vessel. Flow through each of the parallel vessels in Figure 14–10B is determined by the pressure gradient and its own resistance, not the resistance of the other parallel blood vessels. However, increasing the resistance of any of the blood vessels increases the total vascular resistance.

It may seem paradoxical that adding more blood vessels to a circuit reduces the total vascular resist-ance. Many parallel blood vessels, however, make it easier for blood to flow through the circuit because each parallel vessel provides another pathway, or con- ductance, for bloodflow. The total conductance (Ctotal)for blood flow is the sum of the conductance of each parallel pathway:

Ctotal  = C1 + C2 + C3 + C4 . . .

For example, brain, kidney, muscle, gastrointestinal, skin, and coronary circulations are arranged in paral-lel, and each tissue contributes to the overall conduc-tance of the systemic circulation. Blood flow through each tissue is a fraction of the total blood flow (cardiac output) and is determined by the resistance (the recip-rocal of conductance) for blood flow in the tissue, as well as the pressure gradient. Therefore, amputation of a limb or surgical removal of a kidney also removes a parallel circuit and reduces the total vascular conduc-tance and total blood flow (i.e., cardiac output) while increasing total peripheral vascular resistance.

Effect of Blood Hematocrit and Blood Viscosity on Vascular Resistance and Blood Flow

Note especially that another of the important factors in Poiseuille’s equation is the viscosity of the blood. The greater the viscosity, the less the flow in a vessel if all other factors are constant. Furthermore, the vis-cosity of normal blood is about three times as great as the viscosity of water.

But what makes the blood so viscous? It is mainly the large numbers of suspended red cells in the blood, each of which exerts frictional drag against adjacent cells and against the wall of the blood vessel.

Hematocrit. The percentage of the blood that is cells iscalled the hematocrit. Thus, if a person has a hemat-ocrit of 40, this means that 40 per cent of the blood volume is cells and the remainder is plasma. The hema-tocrit of men averages about 42, while that of women averages about 38. These values vary tremendously, depending on whether the person has anemia, on the degree of bodily activity, and on the altitude at which the person resides. These changes in hematocrit are discussed in relation to the red blood cells and their oxygen transport function.

Hematocrit is determined by centrifuging blood in a calibrated tube, as shown in Figure 14–11. The cali-bration allows direct reading of the percentage of cells.

Effect of Hematocrit on Blood Viscosity. The viscosity ofblood increases drastically as the hematocrit increases, as shown in Figure 14–12. The viscosity of whole blood at normal hematocrit is about 3; this means that three times as much pressure is required to force whole blood as to force water through the same blood vessel.

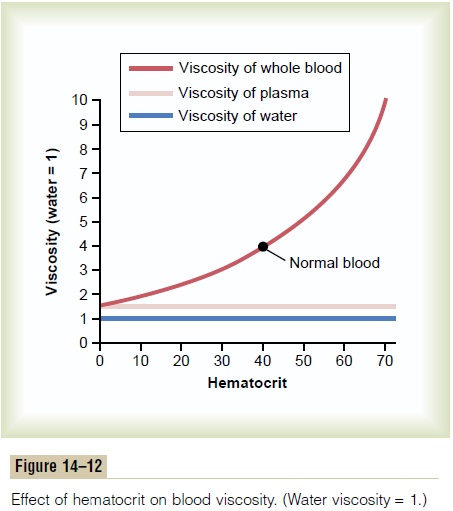
When the hematocrit rises to 60 or 70, which it often does in polycythemia, the blood viscosity can become as great as 10 times that of water, and its flow through blood vessels is greatly retarded.

Other factors that affect blood viscosity are the plasma protein concentration and types of proteins in the plasma, but these effects are so much less than the effect of hematocrit that they are not significant considerations in most hemodynamic studies. The vis-cosity of blood plasma is about 1.5 times that of water.