Chapter: Mechanical : Design of Machine Elements : Steady Stresses and Variable Stresses In Machine Members
Resilience
Resilience
When a body is loaded within elastic limit, it changes its dimensions and on the removal of the load, it regains its original dimensions. So long as it remains loaded, it has stored energy in itself. On removing the load, the energy stored is given off as in the case of a spring. This energy, which is absorbed in a body when strained within elastic limit, is known as strain energy. The strain energy is always capable of doing some work.
The strain energy stored in a body due to external loading, within elastic limit, is known as resilience and the maximum energy which can be stored in a body up to the elastic limit is called proof resilience. The proof resilience per unit volume of a material is known as modulus of resilience.
It is an important property of a material and gives capacity of the material to bear impact or shocks. Mathematically, strain energy stored in a body due to tensile or compressive load or resilience,
U= (σ2 ×V) / 2E
Modulus of resilience = σ2 / 2E
where σ = Tensile or compressive stress, V = Volume of the body, and
= Young's modulus of the material of the body
Torsional Shear Stress
When a machine member is subjected to the action of two equal and opposite couples acting in parallel planes (or torque or twisting moment), then the machine member is said to be subjected to torsion. The stress set up by torsion is known as torsional shear stress. It is zero at the centroidal axis and maximum at the outer surface.
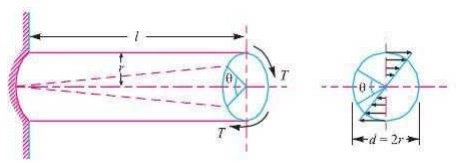
Consider a shaft fixed at one end and subjected to a torque (T) at the other end as shown in Fig. As a result of this torque, every cross-section of the shaft is subjected to torsional shear stress. We have discussed above that the torsional shear stress is zero at the centroidal axis and maximum at the outer surface. The maximum torsional shear stress at the outer surface of the shaft may be obtained from the following equation:
(τ /r) = (T/J) = (Cθ/ l )
where
τ = Torsional shear stress induced at the outer surface of the shaft or maximum shear stress,
= Radius of the shaft,
= Torque or twisting moment,
= Second moment of area of the section about its polar axis or polar moment of inertia,
C = Modulus of rigidity for the shaft material, l = Length of the shaft, and
= Angle of twist in radians on a length l.
Related Topics