Requirements For Message Authentication Codes

REQUIREMENTS FOR MESSAGE AUTHENTICATION CODES

A MAC, also known as a cryptographic checksum, is generated by a function C of the form

T  = MAC(K, M)

where M is a variable-length message, K is a secret key shared only by sender and receiver, and MAC(K, M) is the fixed-length authenticator, sometimes called a tag. The tag is appended to the message at the source at a time when the message is assumed or known to be correct. The receiver authenticates that message by recom- puting the tag.

When an entire message is encrypted for confidentiality, using either  sym- metric or asymmetric encryption, the security of the scheme generally depends on  the bit length of the key. Barring some weakness in the algorithm, the opponent   must resort to a brute-force attack using all possible keys. On average, such an attack will require 2(k - 1) attempts for a  k-bit  key. In  particular, for  a  ciphertext- only attack, the opponent, given ciphertext C, performs Pi = D(Ki, C) for all pos-  sible key values Ki until a Pi is produced that matches the form of acceptable plaintext.

In the case of a MAC, the considerations are entirely different. In general, the MAC function is a many-to-one function, due to the many-to-one nature of the function. Using brute-force methods, how would an opponent attempt to discover a key? If confidentiality is not employed, the opponent has access to plaintext mes- sages and their associated MACs. Suppose k 7 n; that is, suppose that the key size is greater   than   the   MAC   size.   Then,   given   a   known  M1 and T1,   with T1 = MAC(K, M1), the cryptanalyst can perform Ti = MAC(Ki, M1) for all possi- ble key values ki. At least one key is guaranteed to produce a match of Ti = T1. Note that a total of 2k tags will be produced, but there are only 2n 6 2k different tag values. Thus, a number of keys will produce the correct tag and the opponent has no way of knowing which is the correct key. On average, a total of 2k/2n = 2(k - n) keys will produce a match. Thus, the opponent must iterate the attack.

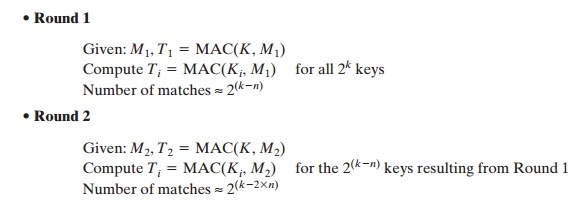
And so on. On average, a rounds will be needed if k = a * n. For example, if an 80-bit key is used and the tab is 32 bits, then the first round will produce about 248 possible keys. The second round will narrow the possible keys to about 216 possibili- ties. The third round should produce only a single key, which must be the one used by the sender.

If the key length is less than or equal to the tag length, then it is likely that a first round will produce a single match. It is possible that more than one key will produce such a match, in which case the opponent would need to perform the same test on a new (message, tag) pair.

Thus, a brute-force attempt to discover the authentication key is no less effort and may be more effort than that required to discover a decryption key of the same length. However, other attacks that do not require the discovery of the key are possible.

Consider the following MAC algorithm. Let M = (X1 || X2 || Á || Xm) be a message that is treated as a concatenation of 64-bit blocks Xi. Then define

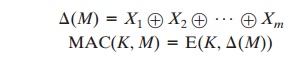
where  Ⓧ  is the exclusive-OR (XOR) operation and the encryption algorithm   is

DES in electronic codebook mode. Thus, the key length is 56 bits, and the tag length is 64 bits. If an opponent observes {M || MAC(K, M)}, a brute-force attempt to determine K will require at least 256 encryptions. But the opponent can attack the system by replacing X1 through Xm - 1 with any desired values Y1 through Ym - 1 and replacing Xm with Ym, where Ym is calculated as

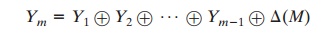
The opponent can now concatenate the new message, which consists of Y1 through Ym, using the original tag to form a message that will be accepted as authen- tic by the receiver. With this tactic, any message of length 64 * (m - 1) bits can be fraudulently inserted.

Thus, in assessing the security of a MAC function, we need to consider the types of attacks that may be mounted against it. With that in mind, let us state the requirements for the function. Assume that an opponent knows the MAC function but does not know K. Then the MAC function should satisfy the following requirements.

1.                                       If an opponent observes M and MAC(K, M), it should be computationally infeasible for the opponent to construct a message M¿ such that

MAC(K,’')   =   MAC(K, M)

2.                                       MAC(K, M) should be uniformly distributed in the sense that for randomly cho- sen messages, M and M¿, the probability that MAC(K, M)   =   MAC(K, M') is 2 - n, where n is the number of bits in the tag.

3.                                       Let M’’’’ be equal to some known transformation on M. That is, M” =  f(M). For example, f may involve inverting one or more specific bits. In that  case,

Pr [MAC(K, M)   =   MAC(K, M')]   =   2 - n

The first requirement speaks to the earlier example, in which an opponent is able to construct a new message to match a given tag, even though the opponent does not know and does not learn the key. The second requirement deals with the need to thwart a brute-force attack based on chosen plaintext. That is, if we assume that the opponent does not know K but does have access to the MAC function and can present messages for MAC generation, then the opponent could try various messages until finding one that matches a given tag. If the MAC function exhibits uniform distribution, then a brute-force method would require, on average, 2(n - 1) attempts before finding a message that fits a given tag.

The final requirement dictates that the authentication algorithm should not be weaker with respect to certain parts or bits of the message than others. If this were not the case, then an opponent who had M and MAC(K, M) could attempt varia- tions on M at the known “weak spots” with a likelihood of early success at producing a new message that matched the old tags.