MACS Based on Block Ciphers: DAA And CMAC

MACS BASED ON BLOCK CIPHERS: DAA AND CMAC

In this section, we look at two MACs that are based on the use of a block cipher mode of operation. We begin with an older algorithm, the Data Authentication Algorithm (DAA), which is now obsolete. Then we examine CMAC, which is designed to overcome the deficiencies of DAA.

Data Authentication Algorithm

The Data Authentication Algorithm (DAA), based on DES, has been one of the most widely used MACs for a number of years. The algorithm is both a FIPS publi- cation (FIPS PUB 113) and an ANSI standard (X9.17). However, as we discuss sub- sequently, security weaknesses in this algorithm have been discovered, and it is being replaced by newer and stronger algorithms.

The algorithm can be defined as using the cipher block chaining (CBC) mode of operation of DES (Figure 6.4) with an initialization vector of zero. The data (e.g., mes- sage, record, file, or program) to be authenticated are grouped into contiguous 64-bit blocks: D1, D2, .... , DN. If necessary, the final block is padded on the right with zeroes to form a full 64-bit block. Using the DES encryption algorithm E and a secret key K, a data authentication code (DAC) is calculated as follows (Figure 12.7).

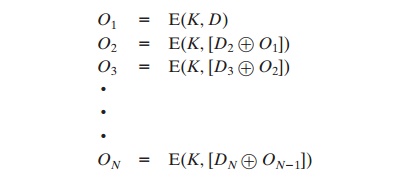
The DAC consists of either the entire block ON or the leftmost M bits of the block, with 16 <= M <= 64.

Cipher-Based Message Authentication Code (CMAC)

As was mentioned, DAA has been widely adopted in government and industry. [BELL00] demonstrated that this MAC is secure under a reasonable set of security criteria, with the following restriction. Only messages of one fixed length of mn bits are processed, where n is the cipher block size and m is a fixed positive integer. As a simple example, notice that given the CBC MAC of a one-block message X, say  T = MAC(K, X), the adversary immediately knows the CBC MAC for the two- block message X || (X { T) since this is once again T.

Black and Rogaway [BLAC00] demonstrated that this limitation could be overcome using three keys: one key of length K to be used at each step of the cipher block chaining and two keys of length n, where k is the key length and n is the cipher block length. This proposed construction was refined by Iwata and Kurosawa so that the two n-bit keys could be derived from the encryption key, rather than being provided separately [IWAT03]. This refinement, adopted by NIST, is the Cipher-based Message Authentication Code (CMAC) mode of oper- ation for use with AES and triple DES. It is specified in NIST Special Publication 800-38B.

First, let us define the operation of CMAC when the message is an integer multiple n of the cipher block length b. For AES, b  = 128, and for triple DES,  b = 64. The message is divided into n blocks (M1, M2, . . . , Mn). The algorithm makes use of a k-bit encryption key K and an n-bit constant, K1. For AES, the key size k is 128, 192, or 256 bits; for triple DES, the key size is 112 or 168 bits. CMAC is calculated as follows (Figure 12.8).

If the message is not an integer multiple of the cipher block length, then the final block is padded to the right (least significant bits) with a 1 and as many 0s as necessary so that the final block is also of length b. The CMAC operation then pro- ceeds as before, except that a different n-bit key K2 is used instead of    K1.

The two n-bit keys are derived from the k-bit encryption key as follows.

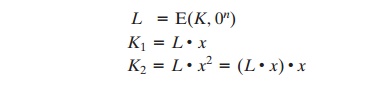
where multiplication ( . ) is done in the finite field GF(2n) and x and x2 are first- and

second-order polynomials that are elements of GF(2n). Thus, the binary representa- tion of x consists of n - 2 zeros followed by 10; the binary representation of x2 con- sists of n - 3 zeros followed by 100. The finite field is defined with respect to an irreducible polynomial that is lexicographically first among all such polynomials with the minimum possible number of nonzero terms. For the two approved block sizes, the polynomials are x64 + x4 + x3 + x + 1 and x128 + x7 + x2 + x    + 1.

To generate K1 and K2, the block cipher is applied to the block that consists entirely of 0 bits. The first subkey is derived from the resulting ciphertext by a left shift of one bit and, conditionally, by XORing a constant that depends on the block size. The second subkey is derived in the same manner from the first subkey. This property of finite fields of the form GF(2n) was explained in the discussion of MixColumns in Chapter 5.