Message Authentication Functions

MESSAGE AUTHENTICATION FUNCTIONS

Any message authentication or digital signature mechanism has two levels of functionality. At the lower level, there must be some sort of function that produces an authenticator: a value to be used to authenticate a message. This lower-level func- tion is then used as a primitive in a higher-level authentication protocol that enables a receiver to verify the authenticity of a message.

This section is concerned with the types of functions that may be used to pro- duce an authenticator. These may be grouped into three classes.

•                           Hash function: A function that maps a message of any length into a fixed- length hash value, which serves as the authenticator

•                           Message encryption: The ciphertext of the entire message serves as its authen- ticator

•                           Message authentication code (MAC): A function of the message and a secret key that produces a fixed-length value that serves as the authenticator

Hash functions, and how they may serve for message authentication, are dis- cussed in Chapter 11. The remainder of this section briefly examines the remaining two topics. The remainder of the chapter elaborates on the topic of MACs.

Message Encryption

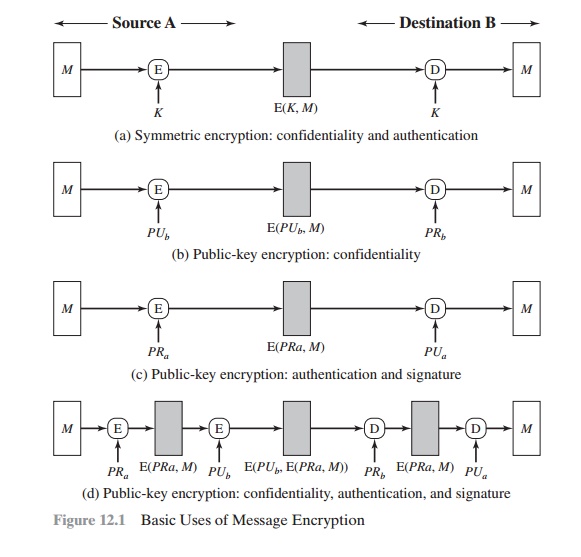
Message encryption by itself can provide a measure of authentication. The analysis differs for symmetric and public-key encryption schemes.

SYMMETRIC ENCRYPTION Consider the straightforward use of symmetric encryption (Figure 12.1a). A message M transmitted from source A to destination B is encrypted using a secret key K shared by A and B. If no other party knows the key, then confidentiality is provided: No other party can recover the plaintext of the message.

In addition, B is assured that the message was generated by A. Why? The mes- sage must have come from A, because A is the only other party that possesses K and therefore the only other party with the information necessary to construct cipher- text that can be decrypted with K. Furthermore, if M is recovered, B knows that none of the bits of M have been altered, because an opponent that does not know K would not know how to alter bits in the ciphertext to produce the desired changes in the plaintext.

So we may say that symmetric encryption provides authentication as well as confidentiality. However, this flat statement needs to be qualified. Consider exactly what is happening at B. Given a decryption function D and a secret key K, the destination will accept any input X and produce output Y = D(K, X). If X is the ciphertext of a legitimate message M produced by the corresponding encryption function, then Y is some plaintext message M. Otherwise, Y will likely be a meaningless sequence of bits. There may need to be some automated means of determining at B whether Y is legitimate plaintext and therefore must have come from A.

The implications of the line of reasoning in the preceding paragraph are pro- found from the point of view of authentication. Suppose the message M can be any arbitrary bit pattern. In that case, there is no way to determine automatically, at the destination, whether an incoming message is the ciphertext of a legitimate message. This conclusion is incontrovertible: If M can be any bit pattern, then regardless of the value of X, the value Y = D(K, X) is some bit pattern and therefore must be accepted as authentic plaintext.

Thus, in general, we require that only a small subset of all possible bit pat- terns be considered legitimate plaintext. In that case, any spurious ciphertext is unlikely to produce legitimate plaintext. For example, suppose that only one bit pattern in 106 is legitimate plaintext. Then the probability that any randomly cho- sen bit pattern, treated as ciphertext, will produce a legitimate plaintext message  is only 10 - 6.

For a number of applications and encryption schemes, the desired conditions prevail as a matter of course. For example, suppose that we are transmitting English- language messages using a Caesar cipher with a shift of one (K = 1). A sends the following legitimate ciphertext:

Nbsftfbupbutboeepftfbupbutboemjuumfmbnctfbujwz

B decrypts to produce the following plaintext:

mareseatoatsanddoeseatoatsandlittlelambseativy

A simple frequency analysis confirms that this message has the profile of ordinary English. On the other hand, if an opponent generates the following random sequence of letters:

zuvrsoevgqxlzwigamdvnmhpmccxiuureosfbcebtqxsxq

this decrypts to

ytuqrndufpwkyvhfzlcumlgolbbwhttqdnreabdaspwrwp

which does not fit the profile of ordinary English.

It may be difficult to determine automatically if incoming ciphertext decrypts to intelligible plaintext. If the plaintext is, say, a binary object file or digitized X-rays, determination of properly formed and therefore authentic plaintext may be diffi- cult. Thus, an opponent could achieve a certain level of disruption simply by issuing messages with random content purporting to come from a legitimate user.

One solution to this problem is to force the plaintext to have some structure that is easily recognized but that cannot be replicated without recourse to the encryption function. We could, for example, append an error-detecting code, also known as a frame check sequence (FCS) or checksum, to each message before encryption, as illustrated in Figure 12.2a. A prepares a plaintext message M and then provides this as input to a function F that produces an FCS. The FCS is appended to  M  and  the  entire block is  then encrypted. At  the  destination, B

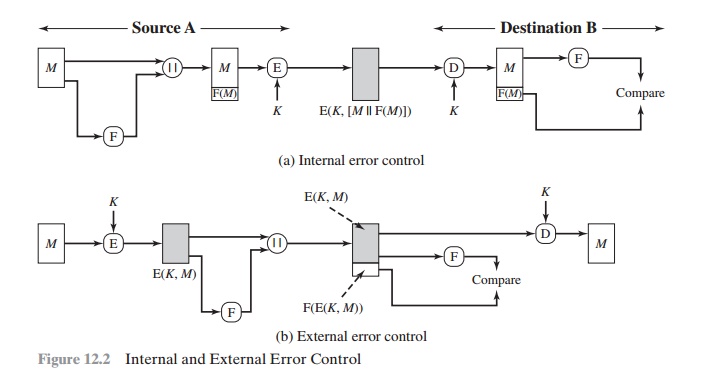
decrypts the incoming block and treats the results as a message with an appended FCS. B applies the same function F to attempt to reproduce the FCS. If the calcu- lated FCS is equal to the incoming FCS, then the message is considered authentic. It is unlikely that any random sequence of bits would exhibit the desired relationship.

Note that the order in which the FCS and encryption functions are performed is critical. The sequence illustrated in Figure 12.2a is referred to in [DIFF79]   as internal error control, which the authors contrast with external error control (Figure 12.2b). With internal error control, authentication is provided because an opponent would have difficulty generating ciphertext that, when decrypted, would have valid error control bits. If instead the FCS is the outer code, an opponent can construct messages with valid error-control codes. Although the opponent cannot know what the decrypted plaintext will be, he or she can still hope to create confu- sion and disrupt operations.

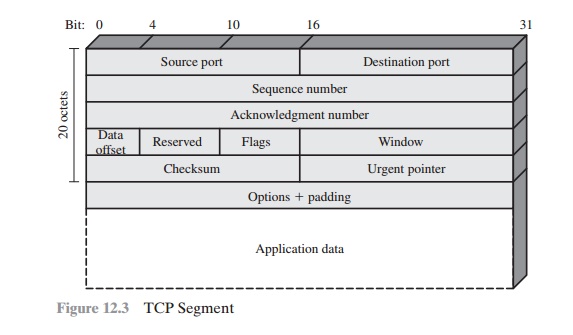
An error-control code is just one example; in fact, any sort of structuring added to the transmitted message serves to strengthen the authentication capability. Such structure is provided by the use of a communications architecture consisting of layered protocols. As an example, consider the structure of messages transmitted using the TCP/IP protocol architecture. Figure 12.3 shows the format of a TCP seg- ment, illustrating the TCP header. Now suppose that each pair of hosts shared a unique secret key, so that all exchanges between a pair of hosts used the same key, regardless of application. Then we could simply encrypt all of the datagram except the IP header. Again, if an opponent substituted some arbitrary bit pattern for the encrypted TCP segment, the resulting plaintext would not include a meaningful header. In this case, the header includes not only a checksum (which covers the header) but also other useful information, such as the sequence number. Because successive TCP segments on a given connection are numbered sequentially, encryp- tion assures that an opponent does not delay, misorder, or delete any segments.

PUBLIC-KEY ENCRYPTION The straightforward use of public-key encryption (Figure 12.1b) provides confidentiality but not authentication. The source (A) uses the public key PUb of the destination (B) to encrypt M. Because only B has the

corresponding private key PRb, only B can decrypt the message. This scheme provides no authentication, because any opponent could also use B’s public key to encrypt a message and claim to be A.

To provide authentication, A uses its private key to encrypt the message, and B uses A’s public key to decrypt (Figure 12.1c). This provides authentication using the same type of reasoning as in the symmetric encryption case: The message must have come from A because A is the only party that possesses PRa and therefore the only party with the information necessary to construct ciphertext that can be decrypted with PUa. Again, the same reasoning as before applies: There must be some internal structure to the plaintext so that the receiver can distinguish between well-formed plaintext and random bits.

Assuming there is such structure, then the scheme of Figure 12.1c does provide authentication. It also provides what is known as digital signature.1 Only A could have constructed the ciphertext because only A possesses PRa. Not even B, the recipient, could have constructed the ciphertext. Therefore, if B is in possession of the ciphertext, B has the means to prove that the message must have come from A. In effect, A has “signed” the message by using its private key to encrypt. Note that this scheme does not provide confidentiality. Anyone in possession of A’s public key can decrypt the ciphertext.

To provide both confidentiality and authentication, A can encrypt M first using its private key, which provides the digital signature, and then using B’s public key, which provides confidentiality (Figure 12.1d). The disadvantage of this approach is that the public-key algorithm, which is complex, must be exercised four times rather than two in each communication.

Message Authentication Code

An alternative authentication technique involves the use of a secret key to generate a small fixed-size block of data, known as a cryptographic checksum or MAC, that is appended to the message. This technique assumes that two communicating parties, say A and B, share a common secret key K. When A has a message to send to B, it calculates the MAC as a function of the message and the key:

MAC  = MAC(K, M)

where

M               = input message

C                = MAC function

K                = shared secret key

MAC = message authentication code

The message plus MAC are transmitted to the intended recipient. The recipient per- forms the same calculation on the received message, using the same secret key, to

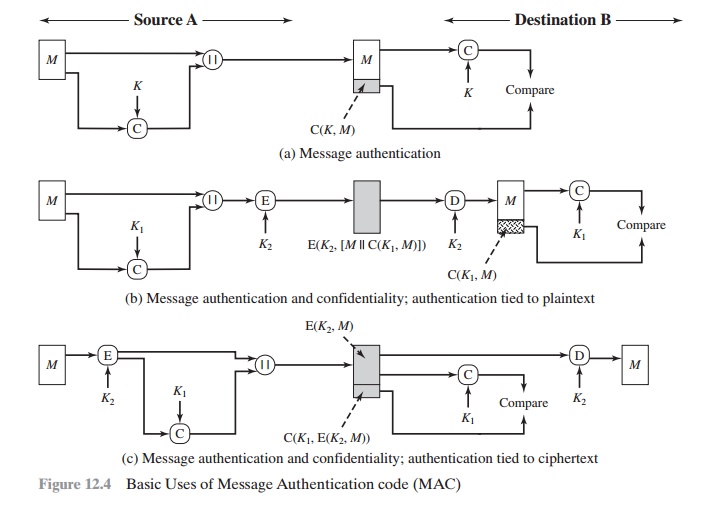
generate a new MAC. The received MAC is compared to the calculated MAC (Figure 12.4a). If we assume that only the receiver and the sender know the identity of the secret key, and if the received MAC matches the calculated MAC, then

1.                                       The receiver is assured that the message has not been altered. If an attacker alters the message but does not alter the MAC, then the receiver’s calculation of the MAC will differ from the received MAC. Because the attacker is assumed not to know the secret key, the attacker cannot alter the MAC to cor- respond to the alterations in the message.

2.                                       The receiver is assured that the message is from the alleged sender. Because no one else knows the secret key, no one else could prepare a message with a proper MAC.

3.                                       If the message includes a sequence number (such as is used with HDLC, X.25, and TCP), then the receiver can be assured of the proper sequence because an attacker cannot successfully alter the sequence number.

A MAC function is similar to encryption. One difference is that the MAC algorithm need not be reversible, as it must be for decryption. In general, the MAC function is a many-to-one function. The domain of the function consists of messages of some arbitrary length, whereas the range consists of all possible MACs and all possible keys. If an n-bit MAC is used, then there are 2n possible MACs, whereas there are N possible messages with N 77 2n. Furthermore, with a k-bit key, there are 2k possible keys.

For example, suppose that we are using 100-bit messages and a 10-bit MAC. Then, there are a total of 2100 different messages but only 210 different MACs. So, on average, each MAC value is generated by a total of 2100/210 = 290 different mes-  sages. If a 5-bit key is used, then there are 25 = 32 different mappings from the set of messages to the set of MAC  values.

It turns out that, because of the mathematical properties of the authentication function, it is less vulnerable to being broken than encryption.

The process depicted in Figure 12.4a provides authentication but not confiden- tiality, because the message as a whole is transmitted in the clear. Confidentiality can be provided by performing message encryption either after (Figure 12.4b) or before (Figure 12.4c) the MAC algorithm. In both these cases, two separate keys are needed, each of which is shared by the sender and the receiver. In the first case, the MAC is calculated with the message as input and is then concatenated to the message. The entire block is then encrypted. In the second case, the message is encrypted first. Then the MAC is calculated using the resulting ciphertext and is concatenated to the ciphertext to form the transmitted block. Typically, it is preferable to tie the authenti- cation directly to the plaintext, so the method of Figure 12.4b is used.

Because symmetric encryption will provide authentication and because it is widely used with readily available products, why not simply use this instead of a sep- arate message authentication code? [DAVI89] suggests three situations in which a message authentication code is used.

1.                        There are a number of applications in which the same message is broadcast to a number of destinations. Examples are notification to users that the network is now unavailable or an alarm signal in a military control center. It is cheaper and more reliable to have only one destination responsible for monitoring authenticity. Thus, the message must be broadcast in plaintext with an associ- ated message authentication code. The responsible system has the secret key and performs authentication. If a violation occurs, the other destination systems are alerted by a general alarm.

2.                        Another possible scenario is an exchange in which one side has a heavy load and cannot afford the time to decrypt all incoming messages. Authentication is carried out on a selective basis, messages being chosen at random for checking.

3.                        Authentication of a computer program in plaintext is an attractive service. The computer program can be executed without having to decrypt it every time, which would be wasteful of processor resources. However, if a message authenti- cation code were attached to the program, it could be checked whenever assur- ance was required of the integrity of the program.

Three other rationales may be added.

For some applications, it may not be of concern to keep messages secret, but it is important to authenticate messages. An example is the Simple Network Management Protocol Version 3 (SNMPv3), which separates the functions of confidentiality and authentication. For this application, it is usually important for a managed system to authenticate incoming SNMP messages, particularly if the message contains a command to change parameters at the managed system. On the other hand, it may not be necessary to conceal the SNMP traffic.

4.                                       Separation of authentication and confidentiality functions affords architectural flexibility. For example, it may be desired to perform authentication at the appli- cation level but to provide confidentiality at a lower level, such as the transport layer.

5.                                       A user may wish to prolong the period of protection beyond the time of recep- tion and yet allow processing of message contents. With message encryption, the protection is lost when the message is decrypted, so the message is pro- tected against fraudulent modifications only in transit but not within the target system.

6.                   Finally, note that the MAC does not provide a digital signature, because both sender and receiver share the same key.