MACS Based on Hash Functions: HMAC

MACS BASED ON HASH FUNCTIONS: HMAC

Later in this chapter, we look at examples of a MAC based on the use of a symmet- ric block cipher. This has traditionally been the most common approach to constructing a MAC. In recent years, there has been increased interest in developing a MAC derived from a cryptographic hash function. The motivations for this interest are

1.                                       Cryptographic hash functions such as MD5 and SHA generally execute faster in software than symmetric block ciphers such as DES.

2.                                       Library code for cryptographic hash functions is widely available.

With the development of AES and the more widespread availability of code for encryption algorithms, these considerations are less significant, but hash-based MACs continue to be widely used.

A hash function such as SHA was not designed for use as a MAC and cannot be used directly for that purpose, because it does not rely on a secret key. There have been a number of proposals for the incorporation of a secret key into an existing hash algorithm. The approach that has received the most support is HMAC [BELL96a, BELL96b]. HMAC has been issued as RFC 2104, has been chosen as the mandatory-to-implement MAC for IP security, and is used in other Internet proto- cols, such as SSL. HMAC has also been issued as a NIST standard (FIPS 198).

HMAC Design Objectives

RFC 2104 lists the following design objectives for  HMAC.

•                           To use, without modifications, available hash functions. In particular, to use hash functions that perform well in software and for which code is freely and widely available.

•                           To allow for easy replaceability of the embedded hash function in case faster or more secure hash functions are found or required.

•                           To preserve the original performance of the hash function without incurring a significant degradation.

•                           To use and handle keys in a simple way.

•                           To have a well understood cryptographic analysis of the strength of the authentication mechanism based on reasonable assumptions about the embedded hash function.

The first two objectives are important to the acceptability of HMAC. HMAC treats the hash function as a “black box.” This has two benefits. First, an existing implementation of a hash function can be used as a module in implementing HMAC. In this way, the bulk of the HMAC code is prepackaged and ready to use without modification. Second, if it is ever desired to replace a given hash function in an HMAC implementation, all that is required is to remove the existing hash func- tion module and drop in the new module. This could be done if a faster hash func- tion were desired. More important, if the security of the embedded hash function were compromised, the security of HMAC could be retained simply by replacing the embedded hash function with a more secure one (e.g., replacing SHA-2 with SHA-3).

The last design objective in the preceding list is, in fact, the main advantage of HMAC over other proposed hash-based schemes. HMAC can be proven   secure provided that the embedded hash function has some reasonable cryptographic strengths. We return to this point later in this section, but first we examine the struc- ture of HMAC.

HMAC Algorithm

Figure 12.5 illustrates the overall operation of HMAC. Define the following terms. H = embedded hash function (e.g., MD5, SHA-1, RIPEMD-160)

IV =  initial value input to hash function

M = message input to HMAC (including the padding specified in the embed- ded hash function)

Yi  = i th block of M,0 Š i Š (L – 1)

L  = number of blocks in M

b = number of bits in a block

n = length of hash code produced by embedded hash function

K = secret key; recommended length is Š n; if key length is greater than b, the key is input to the hash function to produce an n-bit key

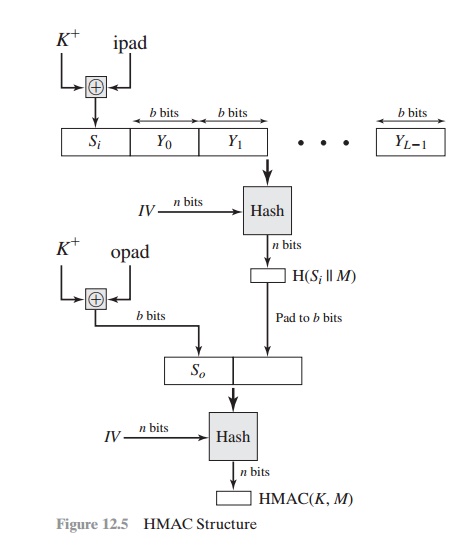
K+ = K padded with zeros on the left so that the result is b bits in length ipad = 00110110 (36 in hexadecimal) repeated b/8 times

opad = 01011100 (5C in hexadecimal) repeated b/8 times Then HMAC can be expressed as

HMAC(K, M)   =   H[(K+ Ⓧ opad) || H[(K+ Ⓧ ipad) || M]]

We can describe the algorithm as follows.

1.                                       Append zeros to the left end of K to create a b-bit string K+ (e.g., if K is of length 160 bits and b = 512, then K will be appended with 44 zeroes).

2.                                       XOR (bitwise exclusive-OR) K+ with ipad to produce the b-bit block Si.

3.                                       Append M to Si.

4.                                       Apply H to the stream generated in step 3.

5.                                       XOR K+ with opad to produce the b-bit block So.

6.                                       Append the hash result from step 4 to So.

7.                                       Apply H to the stream generated in step 6 and output the result.

Note that the XOR with ipad results in flipping one-half of the bits of K. Similarly, the XOR with opad results in flipping one-half of the bits of K, using a dif- ferent set of bits. In effect, by passing Si and So through the compression function of the hash algorithm, we have pseudorandomly generated two keys from K.

HMAC should execute in approximately the same time as the embedded hash function for long messages. HMAC adds three executions of the hash compression function (for Si, So, and the block produced from the inner hash).

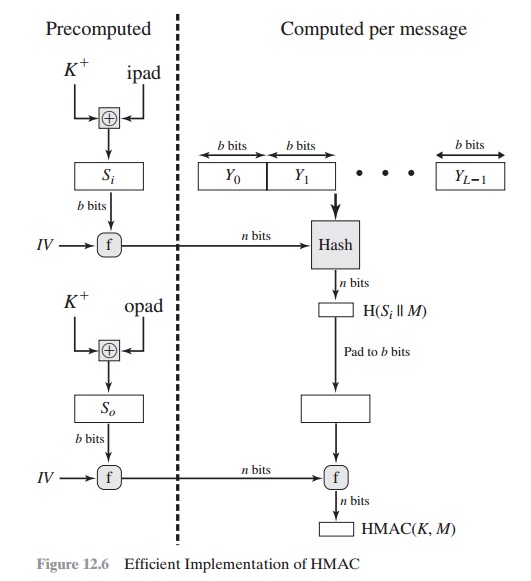
A more efficient implementation is possible, as shown in Figure 12.6. Two

quantities are precomputed:

f(IV, (K + Ⓧ ipad))

f(IV, (K + Ⓧ opad))

where f(cv, block) is the compression function for the hash function, which takes as arguments a chaining variable of n bits and a block of b bits and produces a chaining variable of n bits. These quantities only need to be computed initially and every time the key changes. In effect, the precomputed quantities substitute for the initial value

(IV) in the hash function. With this implementation, only one additional instance of the compression function is added to the processing normally produced by the hash function. This more efficient implementation is especially worthwhile if most of the messages for which a MAC is computed are short.

Security of HMAC

The security of any MAC function based on an embedded hash function depends in some way on the cryptographic strength of the underlying hash function. The appeal of HMAC is that its designers have been able to prove an exact relationship between the strength of the embedded hash function and the strength of   HMAC.

The security of a MAC function is generally expressed in terms of the probability of successful forgery with a given amount of time spent by the forger and a given number of message–tag pairs created with the same key. In essence, it is proved in [BELL96a] that for a given level of effort (time, message–tag pairs) on messages generated by a legitimate user and seen by the attacker, the probability of successful attack on HMAC is equivalent to one of the following attacks on the embedded hash function.

1.                        The attacker is able to compute an output of the compression function even with an IV that is random, secret, and unknown to the attacker.

2.                        The attacker finds collisions in the hash function even when the IV is random and secret.

In the first attack, we can view the compression function as equivalent to the hash function applied to a message consisting of a single b-bit block. For this attack, the IV of the hash function is replaced by a secret, random value of n bits. An attack on this hash function requires either a brute-force attack on the key, which is a level of effort on the order of 2n, or a birthday attack, which is a special case of the second attack, discussed next.

In the second attack, the attacker is looking for two messages M and M¿ that produce the same hash: H(M)  =  H(M¿). This is the birthday attack discussed in Chapter 11. We have shown that this requires a level of effort of 2n/2 for a hash length of n. On this basis, the security of MD5 is called into question, because a level of effort of 264 looks feasible with today’s technology. Does this mean that a 128-bit hash function such as MD5 is unsuitable for HMAC? The answer is no, because of  the following argument. To attack MD5, the attacker can choose any set of messages and work on these off line on a dedicated computing facility to find a collision. Because the attacker knows the hash algorithm and the default IV, the attacker can generate the hash code for each of the messages that the attacker generates. However, when attacking HMAC, the attacker cannot generate message/code pairs off line because the attacker does not know K. Therefore, the attacker must observe   a sequence of messages generated by HMAC under the same key and perform the attack on these known messages. For a hash code length of 128 bits, this requires 264 observed blocks (272 bits) generated using the same key. On a 1-Gbps link, one would need to observe a continuous stream of messages with no change in key for about 150,000 years in order to succeed. Thus, if speed is a concern, it is fully accept- able to use MD5 rather than SHA-1 as the embedded hash function for HMAC.