Relational Model Constraints and Relational Database Schemas

Relational Model Constraints and Relational Database Schemas

So far, we have discussed the characteristics of single relations. In a relational data-base, there will typically be many relations, and the tuples in those relations are usu-ally related in various ways. The state of the whole database will correspond to the states of all its relations at a particular point in time. There are generally many restrictions or constraints on the actual values in a database state. These constraints are derived from the rules in the miniworld that the database represents, as we dis-cussed in Section 1.6.8.

In this section, we discuss the various restrictions on data that can be specified on a relational database in the form of constraints. Constraints on databases can generally be divided into three main categories:

              Constraints that are inherent in the data model. We call these inherent model-based constraints or implicit constraints.

Constraints that can be directly expressed in schemas of the data model, typically by specifying them in the DDL (data definition language, see Section 2.3.1). We call these schema-based constraints or explicit constraints.

                                                    Constraints that cannot be directly expressed in the schemas of the data model, and hence must be expressed and enforced by the application pro-grams. We call these application-based or semantic constraints or business rules.

The characteristics of relations that we discussed in Section 3.1.2 are the inherent constraints of the relational model and belong to the first category. For example, the constraint that a relation cannot have duplicate tuples is an inherent constraint. The constraints we discuss in this section are of the second category, namely, constraints that can be expressed in the schema of the relational model via the DDL. Constraints in the third category are more general, relate to the meaning as well as behavior of attributes, and are difficult to express and enforce within the data model, so they are usually checked within the application programs that perform database updates.

Another important category of constraints is data dependencies, which include functional dependencies and multivalued dependencies. They are used mainly for testing the “goodness” of the design of a relational database and are utilized in a process called normalization, which is discussed in Chapters 15 and 16.

The schema-based constraints include domain constraints, key constraints, constraints on NULLs, entity integrity constraints, and referential integrity constraints.

1. Domain Constraints

Domain constraints specify that within each tuple, the value of each attribute A must be an atomic value from the domain dom(A). We have already discussed the ways in which domains can be specified in Section 3.1.1. The data types associated with domains typically include standard numeric data types for integers (such as short integer, integer, and long integer) and real numbers (float and double-precision float). Characters, Booleans, fixed-length strings, and variable-length strings are also available, as are date, time, timestamp, and money, or other special data types. Other possible domains may be described by a subrange of values from a data type or as an enumerated data type in which all possible values are explicitly listed. Rather than describe these in detail here, we discuss the data types offered by the SQL relational standard in Section 4.1.

2. Key Constraints and Constraints on NULL Values

In the formal relational model, a relation is defined as a set of tuples. By definition, all elements of a set are distinct; hence, all tuples in a relation must also be distinct. This means that no two tuples can have the same combination of values for all their attributes. Usually, there are other subsets of attributes of a relation schema R with the property that no two tuples in any relation state r of R should have the same combination of values for these attributes. Suppose that we denote one such subset of attributes by SK; then for any two distinct tuples t₁ and t₂ in a relation state r of R, we have the constraint that:

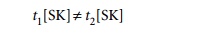
Any such set of attributes SK is called a superkey of the relation schema R. A superkey SK specifies a uniqueness constraint that no two distinct tuples in any state r of R can have the same value for SK. Every relation has at least one default superkey—the set of all its attributes. A superkey can have redundant attributes, however, so a more useful concept is that of a key, which has no redundancy. A key K of a relation schema R is a superkey of R with the additional property that removing any attribute A from K leaves a set of attributes K that is not a superkey of R any more. Hence, a key satisfies two properties:

              Two distinct tuples in any state of the relation cannot have identical values for (all) the attributes in the key. This first property also applies to a superkey.

              It is a minimal superkey—that is, a superkey from which we cannot remove any attributes and still have the uniqueness constraint in condition 1 hold. This property is not required by a superkey.

Whereas the first property applies to both keys and superkeys, the second property is required only for keys. Hence, a key is also a superkey but not vice versa. Consider the STUDENT relation of Figure 3.1. The attribute set {Ssn} is a key of STUDENT because no two student tuples can have the same value for Ssn.⁸ Any set of attrib-utes that includes Ssn—for example, {Ssn, Name, Age}—is a superkey. However, the superkey {Ssn, Name, Age} is not a key of STUDENT because removing Name or Age or both from the set still leaves us with a superkey. In general, any superkey formed from a single attribute is also a key. A key with multiple attributes must require all its attributes together to have the uniqueness property.

The value of a key attribute can be used to identify uniquely each tuple in the rela-tion. For example, the Ssn value 305-61-2435 identifies uniquely the tuple corresponding to Benjamin Bayer in the STUDENT relation. Notice that a set of attributes constituting a key is a property of the relation schema; it is a constraint that should hold on every valid relation state of the schema. A key is determined from the mean-ing of the attributes, and the property is time-invariant: It must continue to hold when we insert new tuples in the relation. For example, we cannot and should not designate the Name attribute of the STUDENT relation in Figure 3.1 as a key because it is possible that two students with identical names will exist at some point in a valid state.⁹

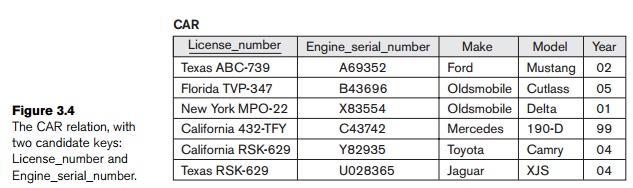
In general, a relation schema may have more than one key. In this case, each of the keys is called a candidate key. For example, the CAR relation in Figure 3.4 has two candidate keys: License_number and Engine_serial_number. It is common to designate one of the candidate keys as the primary key of the relation. This is the candidate key whose values are used to identify tuples in the relation. We use the convention that the attributes that form the primary key of a relation schema are underlined, as shown in Figure 3.4. Notice that when a relation schema has several candidate keys,

the choice of one to become the primary key is somewhat arbitrary; however, it is usually better to choose a primary key with a single attribute or a small number of attributes. The other candidate keys are designated as unique keys, and are not underlined.

Another constraint on attributes specifies whether NULL values are or are not permitted. For example, if every STUDENT tuple must have a valid, non-NULL value for the Name attribute, then Name of STUDENT is constrained to be NOT NULL.

3. Relational Databases and Relational Database Schemas

The definitions and constraints we have discussed so far apply to single relations and their attributes. A relational database usually contains many relations, with tuples in relations that are related in various ways. In this section we define a rela-tional database and a relational database schema.

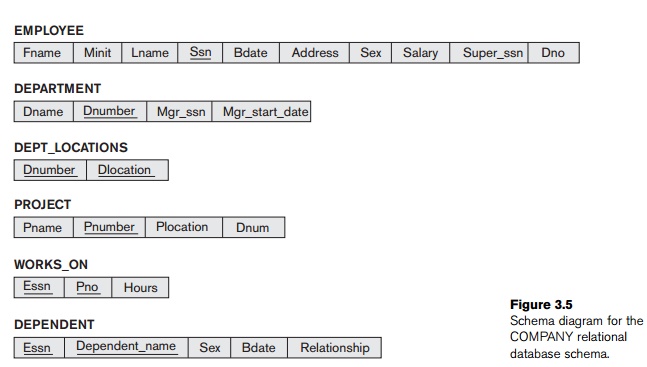
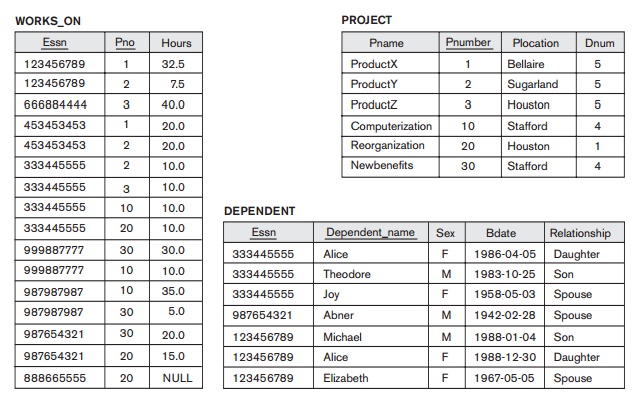
A relational database schema S is a set of relation schemas S = {R₁, R₂, ..., R_m} and a set of integrity constraints IC. A relational database state DB of S is a set of relation states DB = {r₁, r₂, ..., r_m} such that each r_i is a state of R_i and such that the r_i relation states satisfy the integrity constraints specified in IC. Figure 3.5 shows a relational database schema that we call COMPANY = {EMPLOYEE, DEPARTMENT,

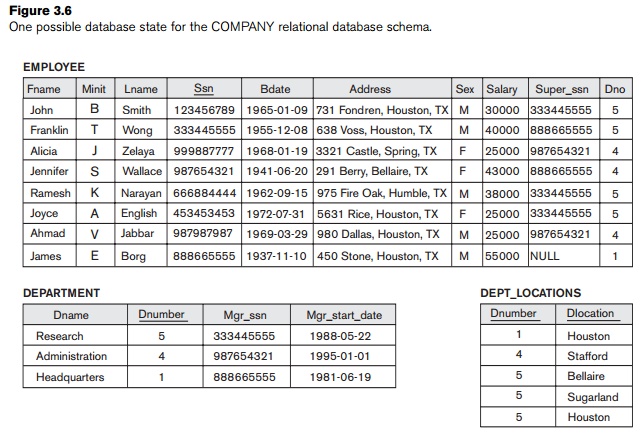
DEPT_LOCATIONS, PROJECT, WORKS_ON, DEPENDENT}. The underlined attributes represent primary keys. Figure 3.6 shows a relational database state corresponding to the COMPANY schema. We will use this schema and database state in this chapter and in Chapters 4 through 6 for developing sample queries in different relational languages. (The data shown here is expanded and available for loading as a populated database from the Companion Website for the book, and can be used for the hands-on project exercises at the end of the chapters.)

When we refer to a relational database, we implicitly include both its schema and its current state. A database state that does not obey all the integrity constraints is

called an invalid state, and a state that satisfies all the constraints in the defined set of integrity constraints IC is called a valid state.

In Figure 3.5, the Dnumber attribute in both DEPARTMENT and DEPT_LOCATIONS stands for the same real-world concept—the number given to a department. That same concept is called Dno in EMPLOYEE and Dnum in PROJECT. Attributes that represent the same real-world concept may or may not have identical names in different relations. Alternatively, attributes that represent different concepts may have the same name in different relations. For example, we could have used the attribute name Name for both Pname of PROJECT and Dname of DEPARTMENT; in this case, we would have two attributes that share the same name but represent different real-world concepts—project names and department names.

In some early versions of the relational model, an assumption was made that the same real-world concept, when represented by an attribute, would have identical attribute names in all relations. This creates problems when the same real-world concept is used in different roles (meanings) in the same relation. For example, the concept of Social Security number appears twice in the EMPLOYEE relation of Figure 3.5: once in the role of the employee’s SSN, and once in the role of the super-visor’s SSN. We are required to give them distinct attribute names—Ssn and Super_ssn, respectively—because they appear in the same relation and in order to distinguish their meaning.

Each relational DBMS must have a data definition language (DDL) for defining a relational database schema. Current relational DBMSs are mostly using SQL for this purpose. We present the SQL DDL in Sections 4.1 and 4.2.

Integrity constraints are specified on a database schema and are expected to hold on every valid database state of that schema. In addition to domain, key, and NOT NULL constraints, two other types of constraints are considered part of the relational model: entity integrity and referential integrity.

4. Integrity, Referential Integrity, and Foreign Keys

The entity integrity constraint states that no primary key value can be NULL. This is because the primary key value is used to identify individual tuples in a relation. Having NULL values for the primary key implies that we cannot identify some tuples. For example, if two or more tuples had NULL for their primary keys, we may not be able to distinguish them if we try to reference them from other relations.

Key constraints and entity integrity constraints are specified on individual relations. The referential integrity constraint is specified between two relations and is used to maintain the consistency among tuples in the two relations. Informally, the referential integrity constraint states that a tuple in one relation that refers to another relation must refer to an existing tuple in that relation. For example, in Figure 3.6, the attribute Dno of EMPLOYEE gives the department number for which each employee works; hence, its value in every EMPLOYEE tuple must match the Dnumber value of some tuple in the DEPARTMENT relation.

To define referential integrity more formally, first we define the concept of a foreign key. The conditions for a foreign key, given below, specify a referential integrity constraint between the two relation schemas R₁ and R₂. A set of attributes FK in rela-tion schema R₁ is a foreign key of R₁ that references relation R₂ if it satisfies the following rules:

              The attributes in FK have the same domain(s) as the primary key attributes PK of R₂; the attributes FK are said to reference or refer to the relation R₂.

              A value of FK in a tuple t₁ of the current state r₁(R₁) either occurs as a value of PK for some tuple t₂ in the current state r₂(R₂) or is NULL. In the former case, we have t₁[FK] = t₂[PK], and we say that the tuple t₁ references or refers to the tuple t₂.

In this definition, R₁ is called the referencing relation and R₂ is the referenced rela-tion. If these two conditions hold, a referential integrity constraint from R₁ to R₂ is said to hold. In a database of many relations, there are usually many referential integrity constraints.

To specify these constraints, first we must have a clear understanding of the mean-ing or role that each attribute or set of attributes plays in the various relation schemas of the database. Referential integrity constraints typically arise from the relationships among the entities represented by the relation schemas. For example, consider the database shown in Figure 3.6. In the EMPLOYEE relation, the attribute Dno refers to the department for which an employee works; hence, we designate Dno to be a foreign key of EMPLOYEE referencing the DEPARTMENT relation. This means that a value of Dno in any tuple t₁ of the EMPLOYEE relation must match a value of

the primary key of DEPARTMENT—the Dnumber attribute—in some tuple t₂ of the DEPARTMENT relation, or the value of Dno can be NULL if the employee does not belong to a department or will be assigned to a department later. For example, in Figure 3.6 the tuple for employee ‘John Smith’ references the tuple for the ‘Research’ department, indicating that ‘John Smith’ works for this department.

Notice that a foreign key can refer to its own relation. For example, the attribute Super_ssn in EMPLOYEE refers to the supervisor of an employee; this is another employee, represented by a tuple in the EMPLOYEE relation. Hence, Super_ssn is a foreign key that references the EMPLOYEE relation itself. In Figure 3.6 the tuple for employee ‘John Smith’ references the tuple for employee ‘Franklin Wong,’ indicating that ‘Franklin Wong’ is the supervisor of ‘John Smith.’

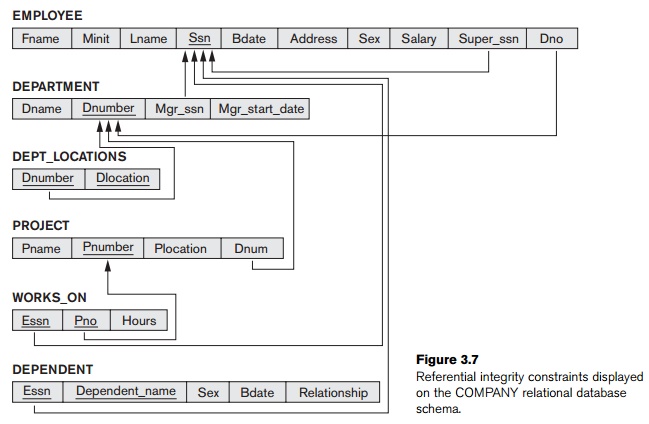
We can diagrammatically display referential integrity constraints by drawing a directed arc from each foreign key to the relation it references. For clarity, the arrowhead may point to the primary key of the referenced relation. Figure 3.7 shows the schema in Figure 3.5 with the referential integrity constraints displayed in this manner.

All integrity constraints should be specified on the relational database schema (i.e., defined as part of its definition) if we want to enforce these constraints on the data-base states. Hence, the DDL includes provisions for specifying the various types of constraints so that the DBMS can automatically enforce them. Most relational DBMSs support key, entity integrity, and referential integrity constraints. These constraints are specified as a part of data definition in the DDL.

5. Other Types of Constraints

The preceding integrity constraints are included in the data definition language because they occur in most database applications. However, they do not include a large class of general constraints, sometimes called semantic integrity constraints, which may have to be specified and enforced on a relational database. Examples of such constraints are the salary of an employee should not exceed the salary of the employee’s supervisor and the maximum number of hours an employee can work on all projects per week is 56. Such constraints can be specified and enforced within the application programs that update the database, or by using a general-purpose constraint specification language. Mechanisms called triggers and assertions can be used. In SQL, CREATE ASSERTION and CREATE TRIGGER statements can be used for this purpose (see Chapter 5). It is more common to check for these types of constraints within the application programs than to use constraint specification languages because the latter are sometimes difficult and complex to use, as we dis-cuss in Section 26.1.

Another type of constraint is the functional dependency constraint, which establishes a functional relationship among two sets of attributes X and Y. This constraint specifies that the value of X determines a unique value of Y in all states of a relation; it is denoted as a functional dependency X → Y. We use functional dependencies and other types of dependencies in Chapters 15 and 16 as tools to analyze the quality of relational designs and to “normalize” relations to improve their quality.

The types of constraints we discussed so far may be called state constraints because they define the constraints that a valid state of the database must satisfy. Another type of constraint, called transition constraints, can be defined to deal with state changes in the database.¹¹ An example of a transition constraint is: “the salary of an employee can only increase.” Such constraints are typically enforced by the application pro-grams or specified using active rules and triggers, as we discuss in Section 26.1.