Chapter: Fundamentals of Database Systems : The Relational Data Model and SQL : The Relational Data Model and Relational Database Constraints
Relational Model Concepts
Relational Model Concepts
The relational model represents the database as a collection of relations. Informally, each relation
resembles a table of values or, to some extent, a flat file of records. It is called a flat file because each record has a simple linear or flat structure. For exam-ple, the
database of files that was shown in Figure 1.2 is similar to the basic
relational model representation. However, there are important differences
between relations and files, as we shall soon see.
When a relation is thought of as a table
of values, each row in the table represents a collection of related data
values. A row represents a fact that typically corresponds to a real-world
entity or relationship. The table name and column names are used to help to
interpret the meaning of the values in each row. For example, the first table
of Figure 1.2 is called STUDENT because each row represents
facts about a particular student entity. The column names—Name, Student_number, Class, and Major—specify how to interpret the data values in each row, based on the
column each value is in. All values in a column are of the same data type.
In the formal relational model terminology, a row is called a tuple, a column header is called an attribute, and the table is called a relation. The data type describing the
types of values that can appear in each column is represented by a domain of possible values. We now
define these terms—domain, tuple,
attribute, and relation—
formally.
1. Domains, Attributes,
Tuples, and Relations
A domain D is a set of atomic values. By atomic we mean that each value in the domain is indivisible as far
as the formal relational model is concerned. A common method of specifying a
domain is to specify a data type from which the data values forming the domain
are drawn. It is also useful to specify a name for the domain, to help in
interpreting its values. Some examples of domains follow:
■ Usa_phone_numbers. The set of ten-digit phone
numbers valid in the United States.
■ Local_phone_numbers. The set
of seven-digit phone numbers valid within a
particular
area code in the United States. The use of local phone numbers is quickly
becoming obsolete, being replaced by standard ten-digit numbers.
■ Social_security_numbers. The set
of valid nine-digit Social Security numbers.
(This is
a unique identifier assigned to each person in the United States for
employment, tax, and benefits purposes.)
Names: The set
of character strings that represent names of persons.
Grade_point_averages.
Possible values of computed grade point averages;
each must
be a real (floating-point) number between 0 and 4.
■ Employee_ages. Possible ages of employees in a
company; each must be an integer
value between 15 and 80.
■ Academic_department_names. The set
of academic department names in a
university,
such as Computer Science, Economics, and Physics.
■ Academic_department_codes. The set
of academic department codes, such as
‘CS’,
‘ECON’, and ‘PHYS’.
The
preceding are called logical
definitions of domains. A data type
or format is also specified for each
domain. For example, the data type for the domain Usa_phone_numbers can be declared as a character
string of the form (ddd)ddd-dddd,
where each d is a numeric (decimal)
digit and the first three digits form a valid
telephone area code. The data type for Employee_ages is an
integer number between 15 and 80. For Academic_department_names, the
data type is the set of all character strings that represent valid department
names. A domain is thus given a name, data type, and format. Additional
information for interpreting the values of a domain can also be given; for
example, a numeric domain such as Person_weights should
have the units of measurement, such as pounds or kilograms.
A relation schema2 R, denoted by R(A1, A2, ..., An), is made up of a relation
name R and a list of attributes, A1, A2, ..., An.
Each attribute Ai is the name of a role played by some domain D in the relation schema R. D
is called the domain of Ai and is denoted by dom(Ai). A
relation schema is used to describe a
relation; R is called the name of this relation. The degree (or arity) of a relation is the number of attributes n
of its relation schema.
A
relation of degree seven, which stores information about university students,
would contain seven attributes describing each student. as follows:
STUDENT(Name, Ssn, Home_phone, Address, Office_phone, Age, Gpa)
Using the
data type of each attribute, the definition is sometimes written as:
STUDENT(Name: string, Ssn: string, Home_phone: string, Address: string,
Office_phone: string, Age: integer, Gpa: real)
For this
relation schema, STUDENT is the
name of the relation, which has seven attributes. In the preceding definition,
we showed assignment of generic types such as string or integer to the
attributes. More precisely, we can specify the following previously defined
domains for some of the attributes of the STUDENT
relation: dom(Name) = Names; dom(Ssn) = Social_security_numbers; dom(HomePhone) = USA_phone_numbers3, dom(Office_phone) = USA_phone_numbers, and dom(Gpa) =
Grade_point_averages. It is also
possible to refer to attributes of a relation schema by their position within the
relation; thus, the second attribute of the STUDENT
rela-tion is Ssn, whereas
the fourth attribute is Address.
A relation (or relation state)4 r
of the relation schema R(A1, A2, ..., An),
also denoted by r(R), is a set of n-tuples r = {t1, t2, ..., tm}.
Each n-tuple
t is an ordered list of n values t =<v1, v2, ..., vn>, where each
value vi, 1 ≤ i ≤ n, is an element of dom (Ai) or is a special NULL value. (NULL values
are discussed further below and in Section
3.1.2.) The ith value in
tuple t, which corresponds to the
attribute Ai, is referred
to as t[Ai] or t.A i
(or t[i] if we use the positional notation). The terms relation intension for the schema R and relation extension for a relation state r(R) are also commonly
used.
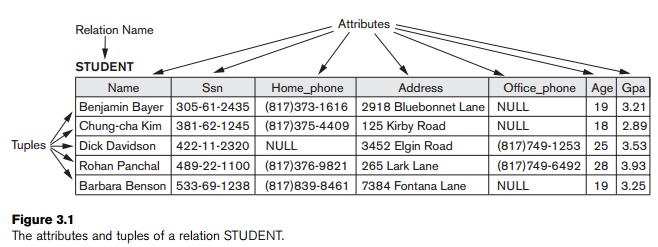
Figure
3.1 shows an example of a STUDENT
relation, which corresponds to the STUDENT
schema
just specified. Each tuple in the relation represents a particular student entity (or object). We
display the relation as a table, where each tuple is shown as a row and each attribute corresponds to a column header indicating a role or
interpretation of the values in that column. NULL values represent attributes whose values are unknown or do not
exist for some individual STUDENT tuple.
The
earlier definition of a relation can be restated
more formally using set theory concepts as follows. A relation (or relation
state) r(R) is a mathematical
relation of degree n on the
domains dom(A1), dom(A2), ..., dom(An), which is a subset of the Cartesian product (denoted by
×) of the domains that define R:
r(R) ⊆ (dom(A1) × dom(A2) × ... × dom(An))
The
Cartesian product specifies all possible combinations of values from the
under-lying domains. Hence, if we denote the total number of values, or cardinality, in a domain D by |D| (assuming that all domains are finite), the total number of
tuples in the Cartesian product is
|dom(A1)| × |dom(A2)| × ... × |dom(An)|
This
product of cardinalities of all domains represents the total number of possible
instances or tuples that can ever exist in any relation state r(R).
Of all these possible combinations, a relation state at a given time—the current relation state—reflects only
the valid tuples that represent a particular state of the real world. In
general, as the state of the real world changes, so does the relation state, by
being transformed into another relation state. However, the schema R is relatively static and changes very infrequently—for example, as a
result of adding an attribute to represent new information that was not originally stored in the relation.
It is
possible for several attributes to have
the same domain. The attribute names indicate different roles, or interpretations, for the
domain. For example, in the STUDENT relation,
the same domain
USA_phone_numbers plays the role of Home_phone, referring to the home phone of a student, and the
role of Office_phone, referring
to the office phone of the student. A
third possible attribute (not shown) with the same domain could be Mobile_phone.
2. Characteristics of
Relations
The earlier definition of relations implies certain characteristics that
make a relation different from a file or a table. We now discuss some of these
characteristics.
Ordering of Tuples in a
Relation. A relation is defined as a set of tuples.
Mathematically, elements of a set have no order among them; hence, tuples in a
relation do not have any particular order. In other words, a relation is not
sensitive to the ordering of tuples. However, in a file, records are physically
stored on disk (or in memory), so there always is an order among the records.
This ordering indicates first, second, ith,
and last records in the file. Similarly, when we display a relation as a table,
the rows are displayed in a certain order.
Tuple ordering is not part of a relation definition because a relation
attempts to rep-resent facts at a logical or abstract level. Many tuple orders
can be specified on the same relation. For example, tuples in the STUDENT relation in Figure 3.1 could be ordered by values of Name, Ssn, Age, or some other attribute. The definition of a relation does not
specify any order: There is no preference
for one ordering over another. Hence, the relation displayed in Figure 3.2 is
considered identical to the one shown
in Figure 3.1. When a relation is implemented as a file or displayed as a
table, a particular ordering may be specified on the records of the file or
the rows of the table.
Ordering of Values within a
Tuple and an Alternative Definition of a Relation. According to the preceding definition of a relation, an n-tuple is an ordered
list of n values, so the ordering of values in a tuple—and hence of
attributes in a relation schema—is
important. However, at a more abstract level, the order of attributes and their
values is not that important as long
as the correspondence between attributes and values is maintained.
An alternative definition of a relation
can be given, making the ordering of values in a tuple unnecessary. In this definition, a relation schema R = {A1,
A2, ..., An} is a set of attributes (instead of a list), and a relation state r(R)
is a finite set of mappings r = {t1, t2, ..., tm},
where each tuple ti is a mapping from
R to D, and D is the union (denoted by ∪) of the
attribute domains; that is, D = dom(A1) ∪ dom(A2)
∪ ... ∪ dom(An). In this definition, t[Ai]
must be in dom(Ai) for 1 ≤ i ≤ n for each mapping t in
r. Each mapping ti is
called a tuple.
According
to this definition of tuple as a mapping, a tuple can be considered as a set
of (<attribute>, <value>) pairs, where each pair gives the value of
the mapping from an attribute Ai
to a value vi from dom(Ai). The ordering of
attributes is not
important, because the attribute
name appears with its value. By
this definition, the two tuples shown in Figure 3.3 are identical. This makes
sense at an abstract level, since there really is no reason to prefer having
one attribute value appear before another in a tuple.
When a relation is implemented as a file, the attributes are physically ordered as fields within a record. We will generally use the first definition of relation, where the attributes and the values within tuples are ordered, because it simplifies much of the notation. However, the alternative definition given here is more general.
Values and NULLs in the Tuples. Each value in a tuple is an atomic value; that is, it is not divisible into components within the framework of the basic relational model. Hence, composite and multivalued attributes (see Chapter 7) are not allowed. This model is sometimes called the flat relational model. Much of the theory behind the relational model was developed with this assumption in mind, which is called the first normal form assumption. Hence, multivalued attributes must be represented by separate relations, and composite attributes are represented only by their simple component attributes in the basic relational model.
An important concept is that of NULL values,
which are used to represent the values of attributes that may be unknown or may
not apply to a tuple. A special value, called NULL, is used
in these cases. For example, in Figure 3.1, some STUDENT tuples
have NULL for their office phones because they do not have an office (that is,
office phone does not apply to these
students). Another student has a NULL for home
phone, presumably because either he does not have a home phone or he has one
but we do not know it (value is unknown).
In general, we can have several meanings for
NULL values, such as value unknown, value exists but is not available, or attribute does not apply to this tuple (also known as
value undefined). An example of the last type
of NULL will occur if we add an attribute Visa_status to the STUDENT relation
Figure 3.3
Two identical tuples when
the order of attributes and values is not part of relation definition.
t = < (Name, Dick Davidson),(Ssn, 422-11-2320),(Home_phone,
NULL),(Address, 3452 Elgin Road), (Office_phone,
(817)749-1253),(Age, 25),(Gpa, 3.53)>
t = < (Address, 3452 Elgin Road),(Name, Dick
Davidson),(Ssn, 422-11-2320),(Age, 25), (Office_phone,
(817)749-1253),(Gpa, 3.53),(Home_phone, NULL)>
that applies only to tuples representing foreign students. It is
possible to devise dif-ferent codes for different meanings of NULL values. Incorporating different types of NULL values
into relational model operations (see Chapter 6) has proven difficult and is outside the scope of our presentation.
The exact meaning of a NULL value governs how it fares
during arithmetic aggrega-tions or comparisons with other values. For example,
a comparison of two NULL values leads to ambiguities—if
both Customer A and B have NULL addresses, it does not
mean they have the same address. During database design, it is best to
avoid NULL values as
much as possible. We will discuss this further in Chapters 5 and 6 in the context of operations and queries, and in Chapter 15 in the context
of database design and normalization.
Interpretation (Meaning) of
a Relation. The relation schema can be
interpreted
as a declaration or a type of assertion. For example, the schema of the STUDENT relation of Figure 3.1 asserts that, in general, a student entity has a
Name, Ssn,
Home_phone,
Address, Office_phone, Age, and
Gpa. Each tuple in the relation can then be interpreted as a fact
or a particular instance of the assertion. For example, the first tuple in
Figure 3.1 asserts the fact that there is a STUDENT whose Name is Benjamin Bayer, Ssn is 305-61-2435, Age is 19, and so on.
Notice that some relations may represent facts about entities, whereas other relations may
represent facts about relationships.
For example, a relation schema MAJORS (Student_ssn, Department_code) asserts that students major in academic disciplines. A tuple in this
relation relates a student to his or her major discipline. Hence, the
rela-tional model represents facts about both entities and relationships uniformly as rela-tions. This sometimes
compromises understandability because one has to guess whether a relation
represents an entity type or a relationship type. We introduce the
Entity-Relationship (ER) model in detail in Chapter 7 where the entity and
relation-ship concepts will be described in detail. The mapping procedures in
Chapter 9 show how different constructs of the ER and EER (Enhanced ER model
covered in Chapter 8) conceptual data models (see Part 3) get converted to
relations.
An alternative interpretation of a relation schema is as a predicate; in this case, the values in
each tuple are interpreted as values that satisfy
the predicate. For example, the predicate STUDENT (Name, Ssn, ...) is true for the five tuples in relation STUDENT of Figure 3.1. These tuples represent five different propositions or
facts in
the real world. This interpretation is quite useful
in the context of logical program-ming languages, such as Prolog, because it
allows the relational model to be used within these languages (see Section
26.5). An assumption called the closed
world assumption states that the
only true facts in the universe are those present within the extension (state) of the relation(s). Any other combination of
values makes the predicate false.
3. Relational Model
Notation
We will
use the following notation in our presentation:
■ A
relation schema R of degree n is denoted by R(A1, A2, ..., An).
The
uppercase letters Q, R, S
denote relation names.
The
lowercase letters q, r, s
denote relation states.
The
letters t, u, v denote tuples.
In
general, the name of a relation schema such as STUDENT also indicates the current set of tuples in that relation—the current relation state—whereas STUDENT(Name, Ssn, ...) refers only to the relation schema.
An
attribute A can be qualified with the
relation name R to which it belongs
by using
the dot notation R.A—for example, STUDENT.Name or STUDENT.Age. This is because the same name
may be used for two attributes in
different relations. However, all attribute names in a particular relation must be distinct.
An n-tuple t in a relation r(R) is denoted by t = <v1, v2, ..., vn>, where vi
is the value corresponding to attribute Ai.
The following notation refers to component
values of tuples:
Both t[Ai]
and t.Ai (and sometimes t[i]) refer to the value vi in t for attribute
Ai.
Both t[Au,
Aw, ..., Az] and t.(Au, Aw, ..., Az), where Au,
Aw, ..., Az is a list of attributes
from R, refer to the subtuple of
values <vu, vw, ..., vz> from t
cor-responding to the attributes specified in the list.
As an example, consider the
tuple t = <‘Barbara Benson’,
‘533-69-1238’, ‘(817)839-8461’, ‘7384 Fontana Lane’, NULL,
19, 3.25> from the STUDENT relation in Figure 3.1; we have t[Name] = <‘Barbara Benson’>, and t[Ssn, Gpa, Age] =
<‘533-69-1238’, 3.25, 19>.
Related Topics