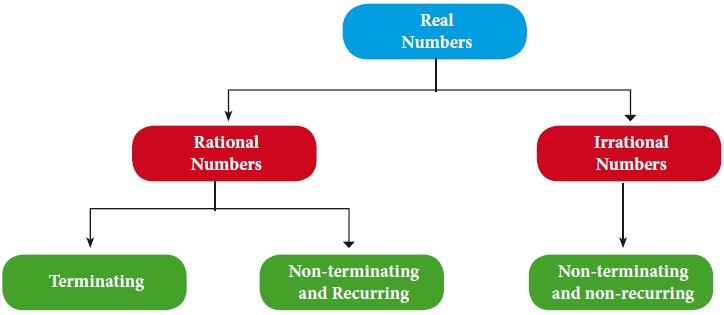
Real Numbers

Real Numbers

The real numbers consist of all the rational numbers and all the irrational numbers.

Real numbers can be thought of as points on an infinitely long number line called the real line, where the points corresponding to integers are equally spaced.

Any real number can be determined by a possibly infinite decimal representation, (as we have already seen decimal representation of the rational numbers and the irrational numbers).

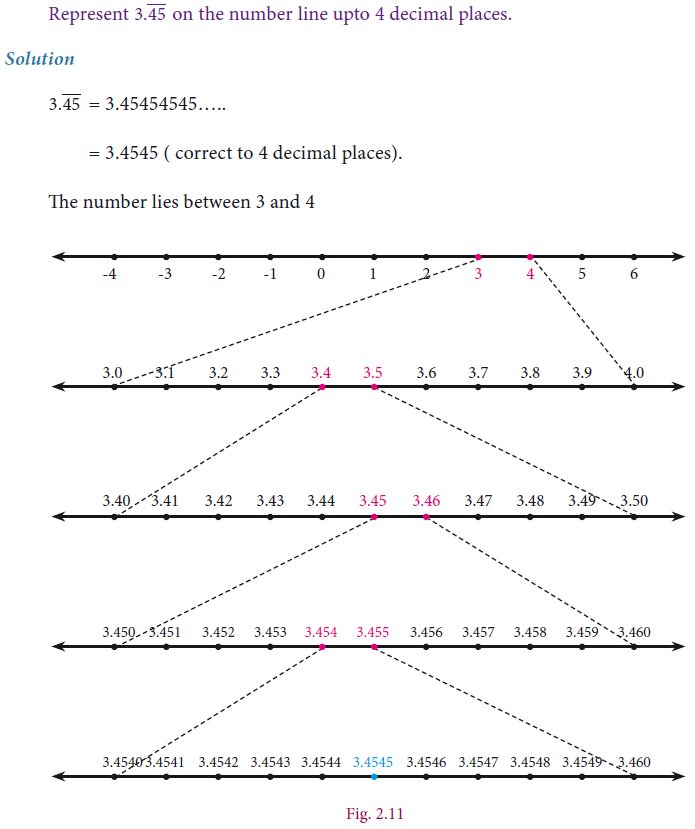
Example 2.14

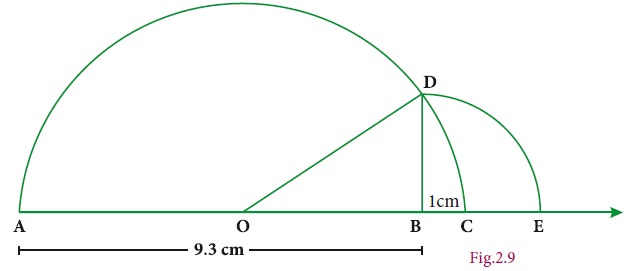
Represent √9.3 on a number line.

Solution

·           Draw a line and mark a point A on it.

·           Mark a point B such that AB = 9.3 cm.

·           Mark a point C on this line such that BC = 1 unit.

·           Find the midpoint of AC by drawing perpendicular bisector of AC and let it be O

·           With O as center and OC = OA as radius, draw a semicircle.

·           Draw a line BD, which is perpendicular to AB at B.

·           Now BD = √9.3 , which can be marked in the number line as the value of BE = BD = √9.3.

1. The Square Root of a Real Number

You have already come across the concept of the square root of a whole number,  decimal fractions etc. While you easily compute values like √169 (which give whole number answers), you also encounter values like √5, √18 , ... etc that yield irrational solutions.

The number 25 has two square roots 5 and –5. However, when we write √25 , we always mean the positive square root 5 (and not the negative square root –5). The symbol √  denotes the positive square root only.

If a is a rational number, any irrational number of the form √a will sometimes be  referred to as a surd. A real number such as 2√3 will be loosely referred to as surd, since it  can be expressed as √12 (How?). We may also say an expression such as √3 + √2  is a surd, although technically we should say that it is a sum of two surd.

Is the number π a surd? No. It cannot be expressed as the root of a rational number, or a finite combination of such numbers.

Recall the basic rules for square roots:

If a,b are positive numbers, then

Example2.15

Find whether x and y are rational or irrational in the following.

2. The Real Number Line

Visualisation through Successive Magnification.

We can visualise the representation of numbers on the number line, as if we glimpse through a magnifying glass.

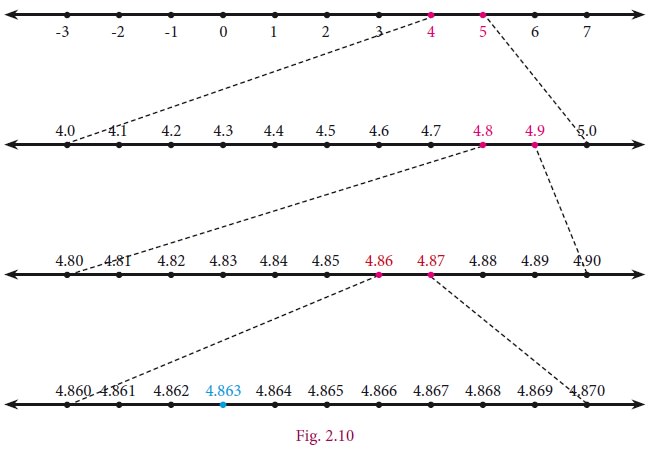
Example 2.16

Represent 4.863 on the number line.

Solution

4.863 lies between 4 and 5(see Fig. 2.10)

1.        Divide the distance between 4 and 5 into 10 equal intervals.

2.        Mark the point 4.8 which is second from the left of 5 and eighth from the right of 4

3.        4.86 lies between 4.8 and 4.9. Divide the distance into 10 equal intervals.

4.        Mark the point 4.86 which is fourth from the left of 4.9 and sixth from the right of 4.8

5.        4.863 lies between 4.86 and 4.87. Divide the distance into 10 equal intervals.

6.        Mark point 4.863 which is seventh from the left of 4.87 and third from the right of 4.86.

Example 2.17