Rational Numbers

Rational Numbers

When you want to count the number of books in your cupboard, you start with 1, 2, 3, … and so on. These counting numbers 1, 2, 3, … , are called Natural numbers. You know to show these numbers on a line (see Fig. 2.1).

We use N to denote the set of all natural numbers.

N= { 1, 2, 3, … }

Suppose there are 5 books in your cupboard and you remove them one by one; the number of books diminish step by step. You remove one, it becomes 4, remove one more, it becomes 3, again one more is removed leaving 2, once again remove one and you are left with 1. If this last one is also taken out, the cupboard is empty (since no books are there). To denote such a situation we use the symbol 0. It denotes absence of any quantity. Thus to say “there are no books”, you can write “the number of books is zero”. Including zero as a digit you can now consider the numbers 0, 1, 2, 3, … and call them Whole numbers. With this additional entity, the number line will look as shown below

We use W to denote the set of all Whole numbers.

W= { 0, 1, 2, 3, … }

Certain conventions lead to more varieties of numbers. Let us agree that certain conventions may be thought of as “positive” denoted by a ‘+’ sign. A thing that is ‘up’ or ‘forward’ or ‘more’ or ‘increasing’ is positive; and anything that is ‘down’ or ‘backward’ or ‘less’ or ‘decreasing’ is “negative” denoted by a ‘–’ sign.

For example, if I make a profit of Rs.1000 in my business, I would call that +1000, and if I lose Rs. 5000, that would be -5000. Why? Similarly, if a mountain’s base is 2 km below sea level and its peak is 3 km above sea level, then the altitude of its base is –2 and the altitude of its peak is +3. (What is its total height? Is it 5 km?).

With this understanding, you can treat natural numbers as positive numbers and rename them as positive integers; thereby you have enabled the entry of negative integers –1, –2, –3, … .

Note that –2 is “more negative” than –1. Therefore, among –1 and –2, you find that –2 is smaller and –1 is bigger. Are –2 and –1 smaller or greater than –3? Think about it.

The number line at this stage may be given as follows:

We use Z to denote the set of all Integers.

Z= { …, –3, –2, –1, 0, 1, 2, 3, … }.

Draw a copy of Fig 2.2. Hold your whole number line up to a mirror on zero. You will see the natural numbers reflected in the mirror. The reflected numbers attached with a minus sign are negative integers. So the numbers to the left of 0 are negative, and the numbers to the right of 0 are positive. But 0 is neither negative nor positive; 0 is just 0. It’s non-committal!

When you look at the figures (Fig. 2.2 and 2.3) above, you are sure to get amused by the gap between any pair of consecutive integers. Could there be some numbers in between?

How did you actually draw the number line N (Fig. 2.1) initially? Draw any line, mark a point 1 on it. From 1, choose another point on its right side at a preferred ‘unit’ distance and call it 2. Repeat this as many times as you desire. To get W (Fig. 2.2), from 1, go one unit on the left to get 0. Now Z is easier; just repeat the exercise on the left side.

You have come across fractions already. How will you mark the point that shows 1/2 on Z? It is just midway between 0 and 1. In the same way, you can plot 1/3, 1/4, 1/5,2 3/4.... etc. You may find that many different fractions are shown by the same point. Can you say ‘why’? Will 5/4 and 10/8 be represented by the same point? Do you think 7/9 and 35/55 represent the same point? You will now easily visualize similar fractions on the left side of zero. These are all fractions of the form a/b  where a and b are integers with one restriction that b ≠ 0. (Why?) If a fraction is in decimal form, even then the setting is same.

Because of the connection between fractions and ratios of lengths, we name them as Rational numbers. Here is a rough picture of the situation:

Since a fraction can have many equivalent fractions , there are many possible names for the same rational number. Thus 1/3, 2/6, 8/24 8 all these denote the same rational number.

1. Denseness Property of Rational Numbers

Consider a, b where a > b and their AM(Arithmetic Mean) given by a+b / 2. Is this AM a rational number? Let us see.

Thus, for any two rational numbers, their average/midpoint is rational. We can repeat this process indefinitely to produce infinitely many rational numbers.

Example 2.1

Find any two rational numbers between 1/2 and 2/3.

Solution 1

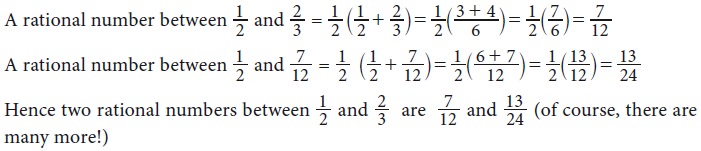
There is an interesting result that could help you to write instantly rational numbers between any two given rational numbers.

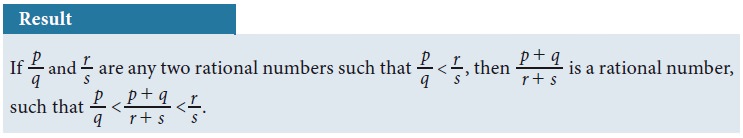
Let us take the same example: Find any two rational numbers between 1/2 and 2/3

Solution 2

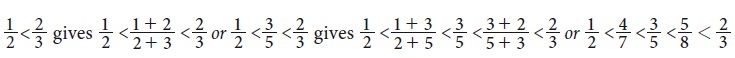
Solution 3

Any more new methods to solve? Yes, if decimals are your favourites, then the above example can be given an alternate solution as follows:

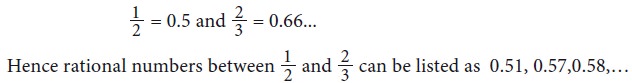
Solution 4