Irrational Numbers

Irrational Numbers

You saw that each rational number is assigned to a point on the number line and learnt about the denseness property of the rational numbers.  Does that mean the line is entirely filled with the rational numbers and there are no more numbers on the number line? Let us explore.

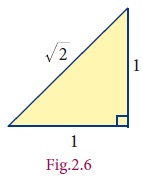
Consider an isosceles right-angled triangle whose legs are each 1 unit long.  Using Pythagoras theorem, the hypotenuse can be seen having a length √(1²+1²) (see Fig. 2.6 ). Greeks found that this √2 is neither a whole number nor an ordinary fraction. The belief of relationship between points on the number line and all numbers was shattered! √2 was called an irrational number.

An irrational number is a number that cannot be expressed as an ordinary ratio of two integers.

A natural question is how one knows that √2 is irrational. It is not difficult to justify it.

If √2 is really rational, let it be equal to p/q where p, q are integers without any common factors (so that p/q will be in its simplest form) and q ≠ 0.

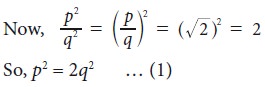
which means p² is even … (2)

As a result, p is even. …. (3)

(Can you prove this?)

Let p = 2m (How?); you get p² = 4m² ;

This, because of (1)

=> 2q² = 4m² or q²=2m².

As a result q is even ` … (4).

(3) and (4) show that p and q have a common factor 2.

This contradicts our assumption that p and q have no common factors and hence  our assumption that √2 can be written as p/q is wrong. That is, √2 is not rational.

Examples

1. Apart from √2 , one can produce a number of examples for such irrational numbers.

Here are a few: √5 , √7, 2√ 3……..

2. π , the ratio of the circumference of a circle to the diameter of that same circle, is  another example for an irrational number.

3. e, also known as Euler’s number, is another common irrational number.

4. Φ , the golden ratio, also known as golden mean, or golden section, is a number often stumbled upon when taking the ratios of distances in simple geometric figures such as the pentagon, the pentagram, decagon and dodecahedron, etc., it is an irrational number.

1. Irrational Numbers on the Number Line

Where are the points on the number line that correspond to the irrational numbers?

As an example, let us locate √2 on the number line. This is easy.

Remember that √2 is the length of the diagonal of the square whose side is 1 unit  (How?)Simply construct a square and transfer the length of one of its diagonals to our number line. (see Fig.2.7).

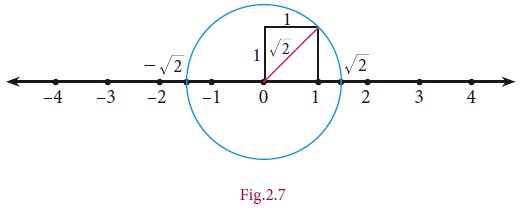
We draw a circle with centre at 0 on the number line,with a radius equal to that of diagonal of the square. This circle cuts the number line in two points, locating √2 on the right of 0 and -√2 on its left. (You wanted to locate √2 ; you have also got a bonus in -√2 )

You started with Natural numbers and extended it to rational numbers and then irrational numbers. You may wonder if further extension on the number line waits for us. Fortunately it stops and you can learn about it in higher classes.

Representation of a Rational number as terminating and non terminating decimal helps us to understand irrational numbers. Let us see the decimal expansion of rational numbers.

2. Decimal Representation of a Rational Number

If you have a rational number written as a fraction, you get the decimal representation by long division. Study the following examples where the remainder is 0 always:

Consider the examples,

Can the decimal representation of a rational number lead to forms of decimals that do not terminate? The following examples (with non-zero remainder) throw some light on this point.

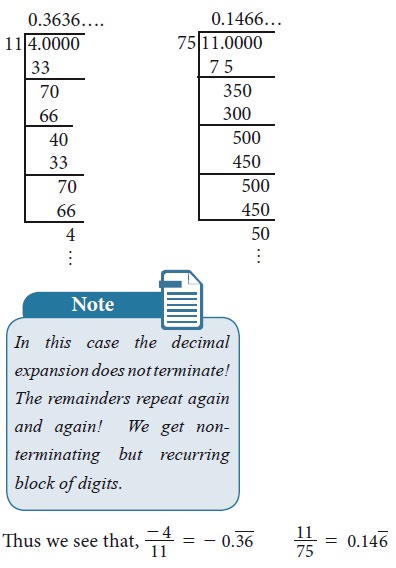
Example 2.2

Represent the following as decimal form (i) -4/11 (ii)11/75

Solution

A rational number can be expressed by

1. either a terminating

2. or a non-terminating and recurring (repeating) decimal expansion.

The converse of this statement is also true.

That is, if the decimal expansion of a number is terminating or non-terminating and recurring, then the number is a rational number.

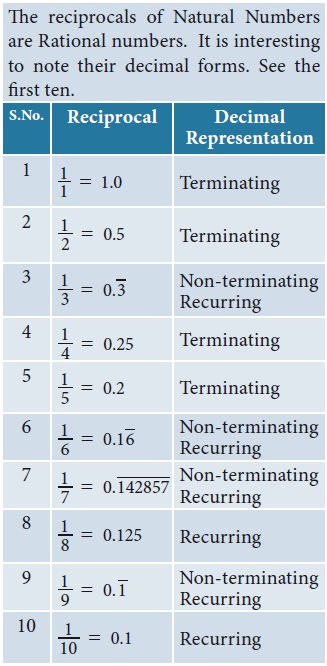
3. Period of Decimal

In the decimal expansion of the rational numbers, the number of repeating decimals is called the length of the period of decimals.

For example,

Example 2.3

4. Conversion of Terminating Decimals into Rational Numbers

Let us now try to convert a terminating decimal, say 2.945 as rational number in the fraction form.

That is, in any decimal number, each digit after the decimal point is a fraction with a denominator in increasing powers of 10. Thus,

Example 2.4

Convert the following decimal numbers in the form of p/q , where p and q are integers and q ≠ 0: (i) 0.35 (ii) 2.176 (iii) – 0.0028

Solution

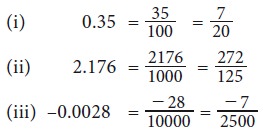
5. ConversionofNon-terminatingandrecurringdecimalsintoRationalNumbers

It was very easy to handle a terminating decimal. When we come across a decimal such as 2.4, we get rid of the decimal point, by just using division by 10.

Thus 2.4 = 24/10 , which is simplified as 12/5. 12 . But, when we have a decimal such as  the problem is that we have infinite number of 4s and hence will need infinite number of 0s in the denominator. For example,

How tough it is to have infinite 4’s and work with them. We need to get rid of the infinite sequence in some way. The good thing about the infinite sequence is that even if we pull away one , two or more 4 out of it, the sequence still remains infinite.

We use the same exact logic to convert any number with a non terminating repeating part into a fraction.

Example 2.5

Convert the following decimal numbers in the form of p/q (p,q∈Z and q≠0)

Example 2.6

Without actual division, classify the decimal expansion of the following numbers as terminating or non – terminating and recurring.

Example 2.7

6. Decimal Representation to Identify Irrational Numbers

It can be shown that irrational numbers, when expressed as decimal numbers, do not terminate, nor do they repeat. For example, the decimal representation of the number π starts with 3.14159265358979, but no finite number of digits can represent π exactly, nor does it repeat.

Consider the following decimal expansions:

(i) 0.1011001110001111…

(ii) 3.012012120121212…

(iii) 12.230223300222333000…

(iv) √2 = 1.4142135624…

Are the above numbers terminating (or) recurring and non- terminating? No… They are neither terminating, nor non–terminating and recurring. Hence they are not rational numbers. They cannot be written in the form of p/q, where p,q, ∈ Z and q≠0. They are irrational numbers.

A number having non- terminating and non- recurring decimal expansion is an irrational number.

Example2.8

Find the decimal expansion of √3

Solution

Thus, by division method, √3 = 1.7320508…

It is found that the square root of every positive non perfect square number is an irrational number. √2, √3, √5, √6, √7 , … are all irrational numbers.

Example 2.9

Classify the numbers as rational or irrational:

Example 2.10

Locate an irrational number between two rational numbers 23/10 and 12/5.

You need an irrational number greater than 2.3 but less than 2.4

One such irrational number is

2.301001000100001000001000000100000001……..

How do you write it?

See the given box for details.

Is this newly found number irrational?

Yes, observe that it is non-terminating and non-recurring.

Can you find an irrational number between 63 and 64 now?

Could it be 63.01001000100001000010000001… … … ?

Between the rational numbers 7.568903 and 7.568904, is it possible that there is this irrational number 7.568903 01 001 0001 00001 000001 0000001… … …?

Example 2.11

Find any 4 irrational numbers between 1/4 and 1/3.

Example 2.12

Find any 3 irrational numbers between 0.12 and 0.13 .

Solution

Three irrational numbers between 0.12 and 0.13 are 0.12010010001…, 0.12040040004…, 0.12070070007…

Example 2.13

Give any two rational numbers lying between 0.5151151115…. and 0.5353353335…

Solution

Two rational numbers between the given two irrational numbers are 0.5152 and 0.5352

For example, when you consider the rational number 4 and the irrational number √5 , then 4 + √5 , 4 – √5 , 4√5 , 4/√5, √5/4........  ------- are all irrational numbers.