Ratio

Ratio

Think about this Situation

Let us consider a situation of cooking rice for two persons. The quantity of rice required for two persons is one cup. To cook every one cup of rice, we need to add two cups of water. Assuming that 8 more guests join for lunch, will the use of ratio help us in handing this situation?

It is possible to trace the origin of the word "ratio" to the Ancient Greek Medieval. Writers used the word proprotio ("proportion") to indicate ratio and proportionalities ("proprotionality") for the equality of ratios. Early translators rendered this into Latin as ratio ("reason"; as in the word "rational")

The number of cups of rice and water required are given below.

In all the cases, the number of cups of water (or) the number of persons is 2 times the number of cups of rice. So, we write

Number of cups of rice : Number of cups of water (or) the number of persons = 1 : 2 Such comparison is called as a Ratio.

Note

● A ratio is a comparison of two quantities.

● A ratio can be written as a fraction; ratios are mostly written in the simplest form.

● In the above example, the ratio of rice to water in terms of the number of cups can be written in three different ways as 1 : 2 or 1/2 or 1 to 2 .

Try these

1. Write the ratio of red tiles to blue tiles and yellow tiles to red tiles.

Answer:

Yellow: 2/7

Blue: 3/7

Red: 2/7

2. Write the ratio of blue tiles to that of red tiles and red tiles to that of total tiles.

Answer:

Blue: 3/8

Red: 5/8

3. Write the ratio of shaded portion to the unshaded portions in the following shapes.

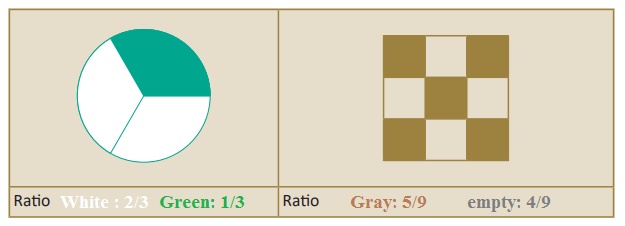
1. Properties of Ratio

● A ratio has no unit. It is a number. For example, the ratio of 8 km to 4 km is written as 8 : 4 = 2 : 1 and not 2 km : 1 km.

● The two quantities of a ratio should be of the same unit. The ratio of 4 km to 400 m is expressed as (4 × 1000) : 400 = 4000 : 400 = 10 : 1

● Each number of the ratio is called a term.

● Order of the terms in a ratio cannot be reversed.

A few examples are given below.

(a) Ratio of the number of small fish to the number of big fish is 5 : 1

(b) Ratio of number of teeth in front gear to number of teeth in back gear is 25 : 50

For example, the ratio of the number of big fish to the number of small fish is 1 : 5. The same information cannot be written as 5 : 1 and so, 1 : 5 and 5 : 1 are not the same.

Similarly, if in a class, there are 12 boys and 12 girls, then the ratio of number of boys to the number of girls is expressed as 12 : 12 which is the same as 1 : 1.

Try this

If the given quantity is in the same unit, put ✓ otherwise put X in the table below.

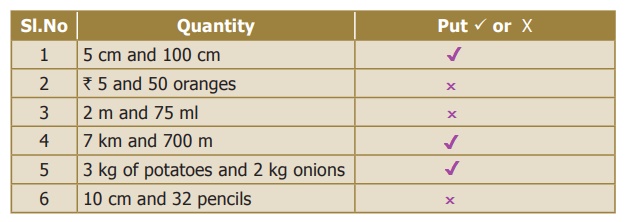
2. Ratios in simplest form

Think about these situations

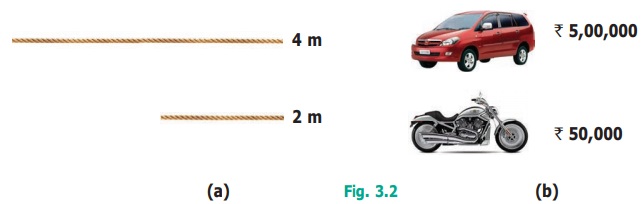
1. The larger rope is 4 m long and the smaller rope is 2 m long. This is expressed in the form of ratio as 4 : 2 and the simplest form of ratio of the larger rope to the smaller rope is 2 : 1 (See Fig. 3.2 (a))

2. The cost of a car is ₹ 5,00,000 and the cost of a motorbike is ₹ 50,000. This is expressed as 500000 : 50000 = 50 : 5 and the simplest form of ratio of the car to the motorbike is 10 : 1 (See Fig. 3.2 (b))

3. Simplifying ratios of same unit

Example 3.1

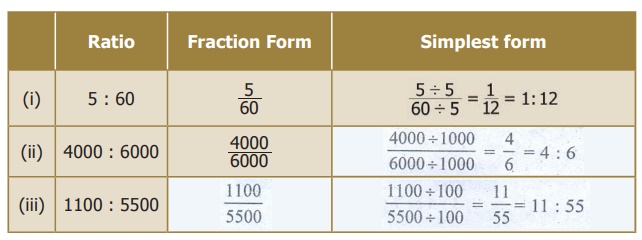
Simplify the ratio 20 : 5.

Solution

Step 1: Write the ratio in fraction form as 20/5.

Step 2: Divide each quantity by 5. That is,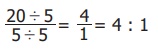 

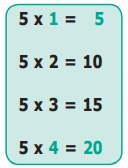
This is the ratio in the simplest form.

Example 3.2

Find the ratio of 500 g to 250 g.

Solution

500 g to 250 g = 500 : 250

 500 /250 = 500÷250 / 250÷250 = 2/1 = 2 : 1

This is the ratio in the simplest form.

Example 3.3

Madhavi and Anbu bought two tables for ₹ 750 and ₹ 900 respectively. What is the ratio of the prices of tables bought by Anbu and Madhavi?

Solution

The ratio of the price, of tables bought by Anbu and Madhavi

= 900:750 = 900 / 750

(900 ÷ 150) / (750 ÷150)  = 6/5 = 6:5

This is the ratio in the simplest form.

4. Simplifying ratios of different units

Example 3.4

What is the ratio of 40 minutes to 1 hour?

Solution

1 hour = 60 minutes

 20 × 1 = 20

 20 × 2 = 40

 20 × 3 = 60

Step 1: Express the quantity in the same unit. (Hint : 1 Hour = 60 minutes)

Step 2: Now, the ratio of 40 minutes to 60 minutes is 40:60

40/60 = 40÷20 / 60÷20 = 2/3 = 2:3

This is the ratio in the simplest form.

Try these

Write the ratios in the simplest form and fill in the table.

5. Equivalent Ratios

We can get equivalent ratios by multiplying or dividing the numerator and denominator by a common number. This is clear from the following example. Let us find the ratio between breadth and length of the following rectangles given in the Figure 3.3

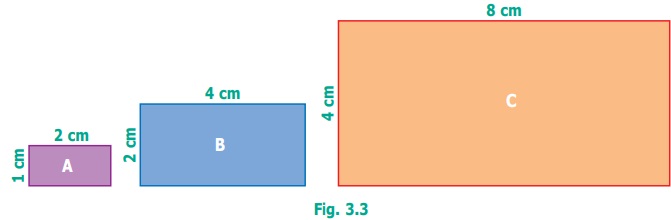
● Ratio of breadth to length of rectangle A is 1 : 2 (already in simplest form)

● Ratio of breadth to length of rectangle B is 2 : 4 (simplest form is 1 : 2)

● Ratio of breadth to length of rectangle C is 4 : 8 (simplest form is 1 : 2)

● Thus, the ratios of breadth and length of rectangles A, B and C are said to be equivalent ratios.

● That is, the ratios 1 : 2 = 2 : 4 = 4 : 8 are equivalent. (See Fig. 3.3)

Try these

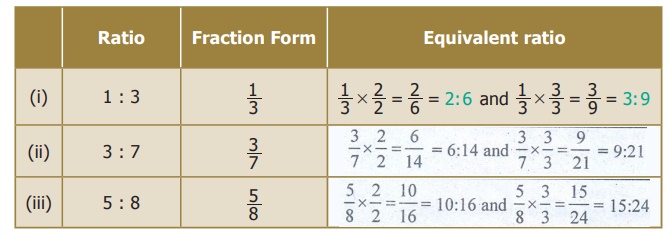
1. For the given ratios, find two equivalent ratios and complete the table.

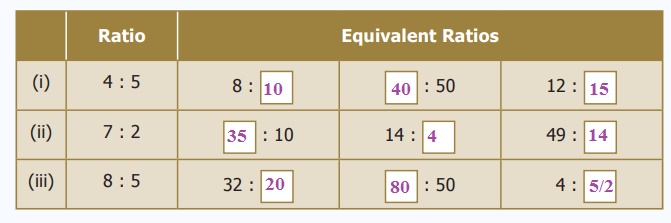
2. Write three equivalent ratios and fill in the boxes.

3. For the given ratios, find their simplest form and complete the table.

6. Comparison of Ratios

Consider the following situations.

Situation 1

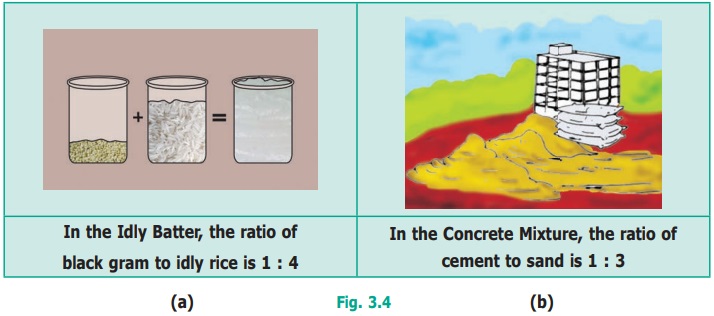
Can you find which ratio is greater in Fig. 3.4?

Express ratios as a fraction and then find the equivalent fractions, until the denominators are the same, and compare the fractions with common denominators. This is done as follows :

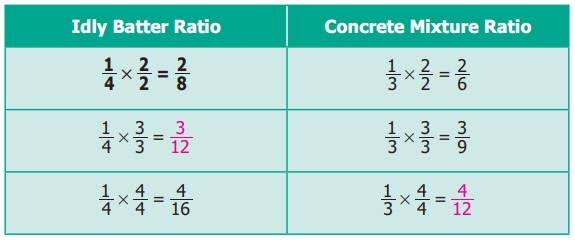
Comparing the equivalent ratios, 4/12 & 3/12, we can conclude that 1 : 3 is greater than 1 : 4

Situation 2

Let us consider another situation. For example, if a thread of 5 m is cut at 3 m, then the length of two pieces are 3 m and 2 m and the ratio of the two pieces is 3 : 2. From this we say that, a ratio ‘a : b’ is said to have a total of ‘a+b’ parts in it.

Example 3.5

Kumaran has ₹ 600 and wants to divide it between Vimala and Yazhini in the ratio 2 : 3. Who will get more and how much?

Solution

Divide the whole money into 2 + 3 = 5 equal parts then, Vimala gets 2 parts out of 5 parts and Yazhini gets 3 parts out of 5 parts.

Amount Vimala gets = ₹ 600 × 2/5 = ₹ 240

Amount Yazhini gets = ₹ 600 × 3/5  = ₹ 360

Vimala received ₹ 240 and Yazhini gets ₹ 360, which is ₹ 120 more than that of Vimala.

ICT Corner

RATIO AND PROPORTION

Expected Result is shown in this picture

Step – 1

Open the Browser and copy and paste the Link given below (or) by typing the URL given (or) Scan the QR Code.

Step − 2

GeoGebra worksheet named “Ratio and Proportion” will open. Two sets of Coloured beads will appear.

Step-3

Find the ratio of coloured beads for each pair. You can Increase or decrease the no’s by pressing “+” and “-“ button appearing on the right side of the page.

Step-4

To check your answer Press on “Pattern 1” and “Pattern 2” button. Repeat the test by increasing and decreasing the beads.

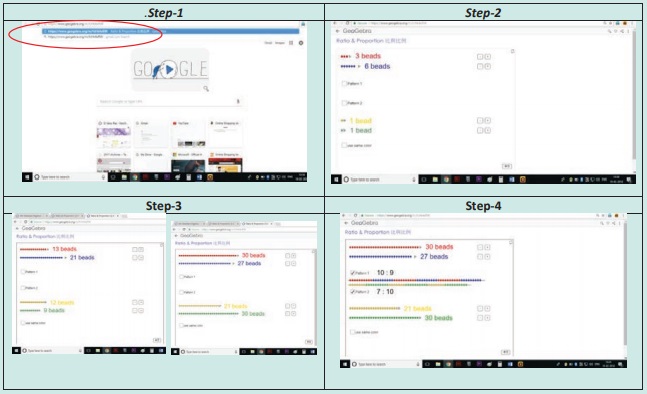
Browse in the link

Ratio and: Proportion − https://www.geogebra.org/m/fcHk4eRW