Equivalent Ratios and Comparison of Ratios

5. Equivalent Ratios

We can get equivalent ratios by multiplying or dividing the numerator and denominator by a common number. This is clear from the following example. Let us find the ratio between breadth and length of the following rectangles given in the Figure 3.3

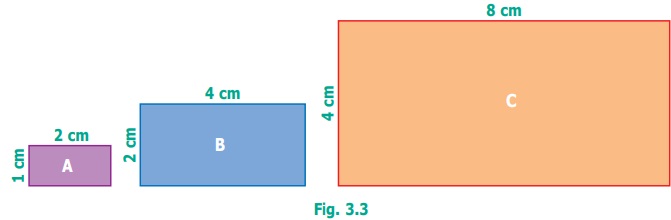
● Ratio of breadth to length of rectangle A is 1 : 2 (already in simplest form)

● Ratio of breadth to length of rectangle B is 2 : 4 (simplest form is 1 : 2)

● Ratio of breadth to length of rectangle C is 4 : 8 (simplest form is 1 : 2)

● Thus, the ratios of breadth and length of rectangles A, B and C are said to be equivalent ratios.

● That is, the ratios 1 : 2 = 2 : 4 = 4 : 8 are equivalent. (See Fig. 3.3)

Try these

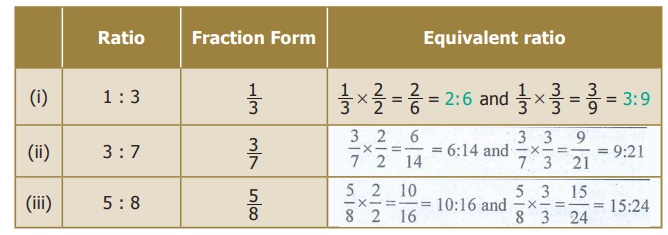
1. For the given ratios, find two equivalent ratios and complete the table.

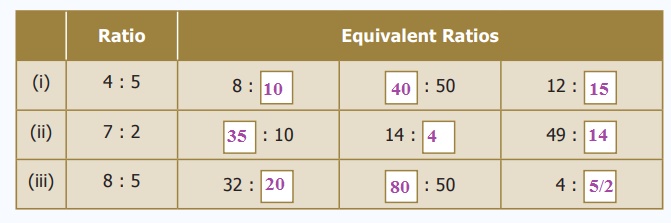
2. Write three equivalent ratios and fill in the boxes.

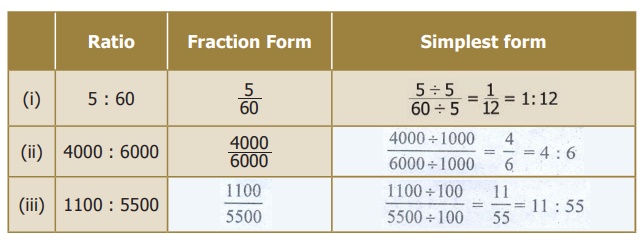
3. For the given ratios, find their simplest form and complete the table.

6. Comparison of Ratios

Consider the following situations.

Situation 1

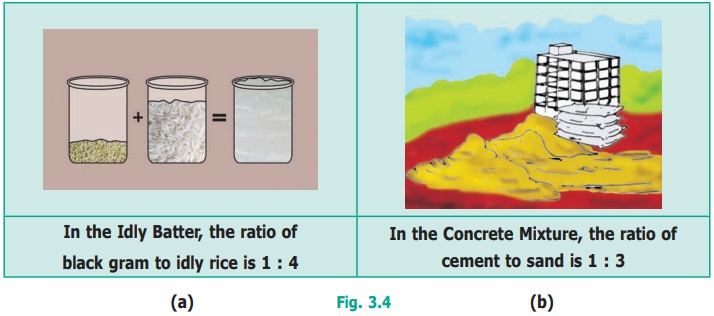
Can you find which ratio is greater in Fig. 3.4?

Express ratios as a fraction and then find the equivalent fractions, until the denominators are the same, and compare the fractions with common denominators. This is done as follows :

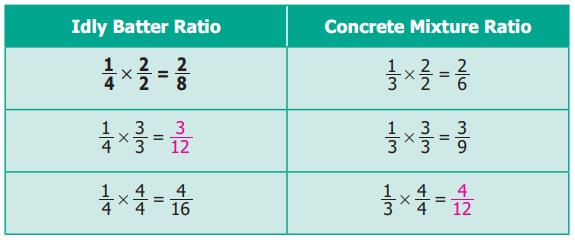
Comparing the equivalent ratios, 4/12 & 3/12, we can conclude that 1 : 3 is greater than 1 : 4

Situation 2

Let us consider another situation. For example, if a thread of 5 m is cut at 3 m, then the length of two pieces are 3 m and 2 m and the ratio of the two pieces is 3 : 2. From this we say that, a ratio ‘a : b’ is said to have a total of ‘a+b’ parts in it.

Example 3.5

Kumaran has ₹ 600 and wants to divide it between Vimala and Yazhini in the ratio 2 : 3. Who will get more and how much?

Solution

Divide the whole money into 2 + 3 = 5 equal parts then, Vimala gets 2 parts out of 5 parts and Yazhini gets 3 parts out of 5 parts.

Amount Vimala gets = ₹ 600 × 2/5 = ₹ 240

Amount Yazhini gets = ₹ 600 × 3/5  = ₹ 360

Vimala received ₹ 240 and Yazhini gets ₹ 360, which is ₹ 120 more than that of Vimala.