Query Processing and Optimization (QPO)

Query Processing and Optimization (QPO)

Basic idea of QPO

In SQL, queries are expressed in high level declarative form

                         QPO translates a SQL query to an execution plan

• over physical data model

• using operations on file-structures, indices, etc.

Ideal execution plan answers Q in as little time as possible

A ROLLBACK does exactly the opposite of COMMIT. It ends the transaction but undoes any changes made during the transaction. All transaction locks acquired on tables are released.

Constraints: QPO overheads are small

• Computation time for QPO steps << that for execution plan

Three Key Concepts in QPO

Building blocks

Most cars have few motions, e.g. forward, reverse

Similar most DBMS have few building blocks:

• select (point query, range query), join, sorting, ...

  A SQL queries is decomposed in building blocks 2. Query processing strategies for building blocks

Cars have a few gears for forward motion: 1st, 2nd, 3rd, overdrive

DBMS keeps a few processing strategies for each building block

• e.g. a point query can be answer via an index or via scanning data-file 3. Query optimization

Automatic transmission tries to picks best gear given motion parameters

For each building block of a given query, DBMS QPO tries to choose

•        ―Most   efficient‖   strategy   given   data

•        Parameter   examples:   Table   size,   avai

Ex. Index search is chosen for a point query if the index is available

QPO Challenges

Choice of building blocks

SQL Queries are based on relational algebra (RA)

Building blocks of RA are select, project, join

• Details in section 3.2 (Note symbols sigma, pi and join) SQL3 adds new building blocks like transitive closure

• Will be discussed in chapter 6

Choice of processing strategies for building blocks

Too many strategies=> higher complexity

Commercial DBMS have a total of 10 to 30 strategies

• 2 to 4 strategies for each building block

How  to   choose   the   ―best‖icable ones?strategy   from   amo

May use a fixed priority scheme

May use a simple cost model based on DBMS parameters

QPO Challenges in SDBMS

Building Blocks for spatial queries

Rich set of spatial data types, operations

A consensus   on   ―building   blocks‖   is   lac

  Current choices include spatial select, spatial join, nearest neighbor Choice of strategies

  Limited choice for some building blocks, e.g. nearest neighbor Choosing best strategies

Cost models are more complex since

•        Spatial Queries are both CPU and I/O intensive

•        while traditional queries are I/O intensive

Cost models of spatial strategies are in not mature.

Query Processing and Optimizer process

•         A site-seeing trip

•         Start : A SQL Query

•         End: An execution plan

•         Intermediate Stopovers

•         query trees

•         logical tree transforms

•         strategy selection

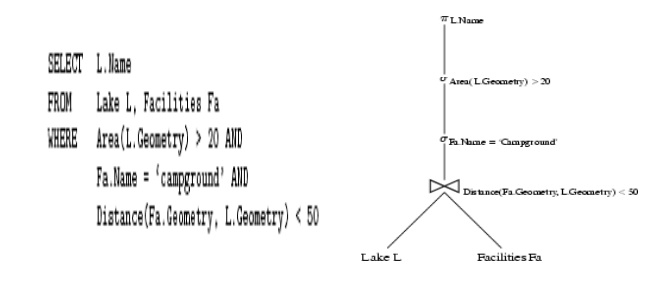
Query Trees

•         Nodes = building blocks of (spatial) queries

•       symbols sigma, pi and join

•           Children = inputs to a building block

•           Leafs = Tables

Example SQL query and its query tree follows:

Logical Transformation of Query Trees

•         Motivation

•         Transformation do not change the answer of the query

•         But can reduce computational cost by

•           reducing data produced by sub-queries

•           reducing computation needs of parent node

•           Example Transformation

•         Push down select operation below join

•         Example: Fig. 5.4 (compare w/ Fig 5.3, last slide)

•         Reduces size of table for join operation

•           Other common transformations

•         Push project down

•         Reorder join operations

•         Traditional logical transform rules

•       For relational queries with simple data types and operations

•           CPU costs are much smaller and I/O costs

•         Need to be reviewed for spatial queries

•           complex data types, operations

•           CPU cost is higher

•           Execution Plans

An execution plan has 3 components

A query tree

A strategy selected for each non-leaf node

An ordering of evaluation of non-leaf nodes

Query Decomposition

Normalization

o manipulate query quantifiers and qualification

Analysis

o detect and reject ―incorrect‖ queries o possible for only a subset of relational calculus

Simplification

o eliminate redundant predicates Restructuring

o calculus query Þ algebraic query

o more than one translation is possible o use transformation rules

Trends in Query Processing and Optimization

Motivation

SDBMS and GIS are invaluable to many organizations

Price of success is to get new requests from customers

•         to support new computing hardware and environment

•         to support new applications

New computing environments

Distributed computing

Internet and web

Parallel computers

New applications

Location based services, transportation

Data Mining

Raster data

Distributed Spatial Databases

Distributed Environments

Collection of autonomous heterogeneous computers

Connected by networks

Client-server architectures

•         Server computer provides well-defined services

•         Client computers use the services

New issues for SDBMS

Conceptual data model -

• Translation between heterogeneous schemas Logical data model

•         Naming and querying tables in other SDBMSs

•         Keeping copies of tables (in other SDBMs) consistent with original table

Query Processing and Optimization

•         Cost of data transfer over network may dominate CPU and I/O costs

•         New strategies to control data transfer costs

ⁿ        Process for heuristics optimization

1.     The parser of a high-level query generates an initial internal representation;

2.     Apply heuristics rules to optimize the internal representation.

3.     A query execution plan is generated to execute groups of operations based on the access paths available on the files involved in the query.

ⁿ        The main heuristic is to apply first the operations that reduce the size of intermediate results.

E.g., Apply SELECT and PROJECT operations before applying the JOIN or other binary operations.

ⁿ        Query tree:

ⁿ        A tree data structure that corresponds to a relational algebra expression. It represents the input relations of the query as leaf nodes of the tree, and represents the relational

algebra operations as internal nodes.

ⁿ        An execution of the query tree consists of executing an internal node operation whenever its operands are available and then replacing that internal node by the relation that results from

executing the operation.

Query graph

 A graph data structure that corresponds to a relational calculus expression. It does not indicate an order on which operations to perform first. There is only a single graph corresponding to each query.

ⁿ        Example:

ⁿ        For every project located in “Stafford department number and the department ma

ⁿ        Relation algebra:

pPNUMBER,             DNUM,   LNAME,    ADDRESS,        BDATE                    (((sPLOCATION=“STAFFORD‘(PROJECT))

_DNUM=DNUMBER (DEPARTMENT))    _MGRSSN=SSN (EMPLOYEE))

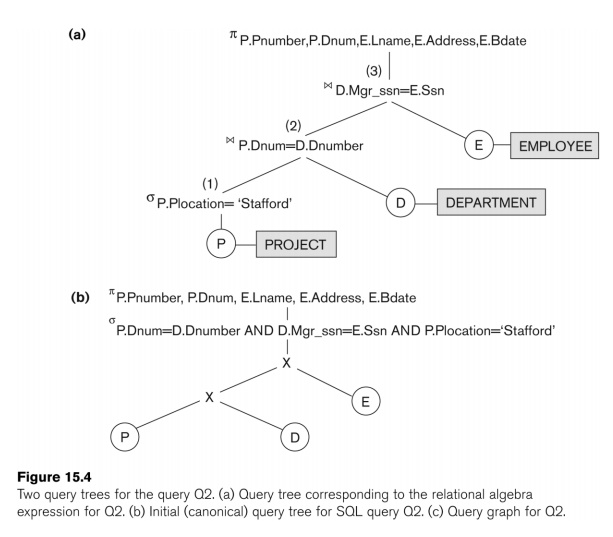
P.PLOCATION=“STAFFORD‘;

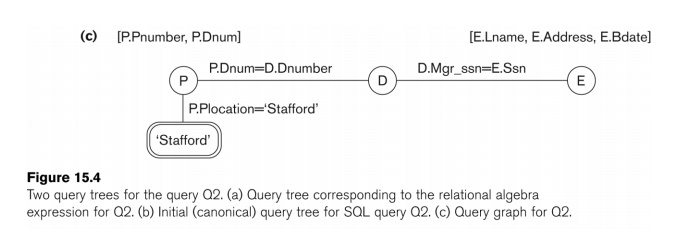
Heuristic Optimization of Query Trees:

ⁿ        The same query could correspond to many different relational algebra expressions — and hence many different query trees.

ⁿ        The task of heuristic optimization of query trees is to find a final query tree that is efficient to execute. 

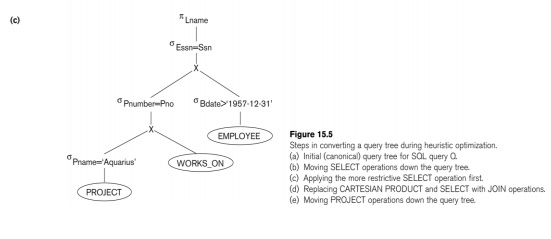
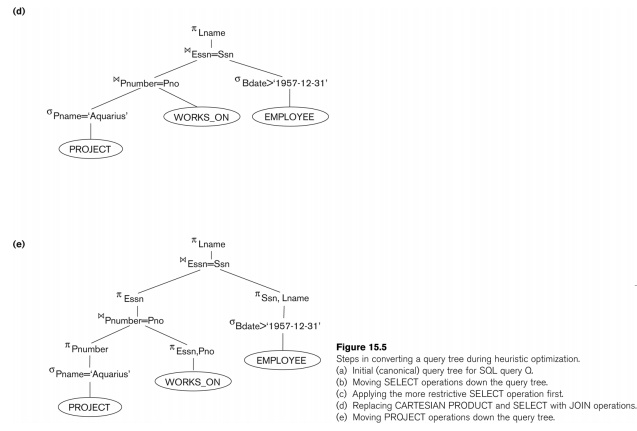
ⁿ        General Transformation Rules for Relational Algebra Operations:

1. Cascade of s: A conjunctive selection condition can be broken up into a cascade (sequence) of individual s operations:

ⁿ        s _{c1 AND c2 AND ... AND cn}(R) = s_c1 (s_c2 (...(s_cn(R))...) )

2. Commutativity of s: The s operation is commutative:

ⁿ        s_c1 (s_c2(R)) = s_c2 (s_c1(R))

3. Cascade of p: In a cascade (sequence) of p operations, all but the last one can be ignored:

ⁿ        p_List1 (p_List2 (...(p_Listn(R))...) ) = p_List1(R)

4. Commuting s with p: If the selection condition c involves only the attributes A1, ..., An in the projection list, the two operations can be commuted:

pA1, A2, ..., An (sc (R)) = sc (pA1, A2, ..., An (R))

. Commutativity of   ( and x ): The   operation is commutative as is the x operation:

^ R   _C S = S   _C R; R x S = S x R

6. Commuting s with   (or x ): If all the attributes in the selection condition c involve only the attributes of one of the relations being joined—say, R—the two operations can be commuted as follows:

 s_c ( R   S ) = (s_c (R))   S

n     Alternatively, if the selection condition c can be written as (c1 and c2), where condition c1 involves only the attributes of R and condition c2 involves only the attributes of S, the operations commute as follows:

n      s_c ( R   S )         = (s_c1 (R))   (sc2 (S))

n     Commuting p with         (or x): Suppose that the projection list is L = {A1, ..., An, B1, ..., Bm},

where A1, ..., An are attributes of R and B1, ..., Bm are attributes of S. If the join condition c involves only attributes in L, the two operations can be commuted as follows:

^ p_L ( R   _C S )  = (p_{A1, ..., An} (R))   _C (p _{B1, ..., Bm} (S))

ⁿ        If the join condition C contains additional attributes not in L, these must be added to the projection list, and a final p operation is needed.

Commutativity of set operations:   The   set   operations–‖is notυ

9. Associativity of , x, υ, and ∩ : Th if q stands for any one of these four operations (throughout the expression), we have

^ ( R q S ) q T  = R q ( S q T )

10. Commuting s with set operations:–.IfqstandsThe s for any one of these three operations, we have

^ s_c ( R q S )  = (s_c (R)) q (s_c (S))

^ The   p   operation   commutes   withp_L(  υR. υ  _LS(R))  =υ

(p_L (S))

^ Converting a (s, x) sequence into : If the condition c of a s that follows a x Corresponds to a join condition, convert the (s, x) sequence into a as follows:

(s_C (R x S))  = (R   _C S)

 Other transformations

Outline of a Heuristic Algebraic Optimization Algorithm:

1.     Using rule 1, break up any select operations with conjunctive conditions into a cascade of select operations.

2.     Using rules 2, 4, 6, and 10 concerning the commutativity of select with other operations, move each select operation as far down the query tree as is permitted by the attributes involved in the select condition.

3.     Using rule 9 concerning associativity of binary operations, rearrange the leaf nodes of the tree so that the leaf node relations with the most restrictive select operations are executed first in the query tree representation.

4.     Using Rule 12, combine a Cartesian product operation with a subsequent select operation in the tree into a join operation.

5.     Using rules 3, 4, 7, and 11 concerning the cascading of project and the commuting of project with other operations, break down and move lists of projection attributes down the tree as far as possible by creating new project operations as needed.

Identify subtrees that represent groups of operations that can be executed by a single algorithm.

ⁿ          Heuristics for Algebraic Optimization:

1.     The main heuristic is to apply first the operations that reduce the size of intermediate results.

2.     Perform select operations as early as possible to reduce the number of tuples and perform project operations as early as possible to reduce the number of attributes. (This is done by moving select and project operations as far down the tree as possible.)

3.     The select and join operations that are most restrictive should be executed before other similar operations. (This is done by reordering the leaf nodes of the tree among themselves and adjusting the rest of the tree appropriately.)

ⁿ        Query Execution Plans

1.     An execution plan for a relational algebra query consists of a combination of the relational algebra query tree and information about the access methods to be used for each relation as well as the methods to be used in computing the relational operators stored in the tree.

2.     Materialized evaluation: the result of an operation is stored as a temporary relationPipelined evaluation: as the result of an operator is produced, it is forwarded to the next operator in sequence.

ⁿ        Cost-based query optimization:

ⁿ        Estimate and compare the costs of executing a query using different execution strategies and choose the strategy with the lowest cost estimate.

ⁿ        (Compare to heuristic query optimization)

ⁿ        Issues

ⁿ        Cost function

Number of execution strategies to be considered

ⁿ        Cost Components for Query Execution

1.     Access cost to secondary storage

2.     Storage cost

3.     Computation cost

4.     Memory usage cost

5.     Communication cost

ⁿ        Note: Different database systems may focus on different cost components.

ⁿ        Catalog Information Used in Cost Functions

1.     Information about the size of a file

ⁿ        number of records (tuples) (r),

ⁿ        record size (R),

ⁿ        number of blocks (b)

ⁿ        blocking factor (bfr)

2.     Information about indexes and indexing attributes of a file

ⁿ        Number of levels (x) of each multilevel index

ⁿ        Number of first-level index blocks (bI1)

ⁿ        Number of distinct values (d) of an attribute

ⁿ        Selectivity (sl) of an attribute

ⁿ        Selection cardinality (s) of an attribute. (s = sl * r)

ⁿ        Examples of Cost Functions for SELECT

ⁿ        S1. Linear search (brute force) approach

1.     C_S1a = b;

2.     For an equality condition on a key, C_S1a = (b/2) if the record is found; otherwise C_S1a = b.

ⁿ        S2. Binary search:

1.     C_S2 = log₂b + (s/bfr)–For an equality condition on a unique (key) attribute, C_S2 =log₂b

ⁿ        S3. Using a primary index (S3a) or hash key (S3b) to retrieve a single record

1.     C_S3a = x + 1; C_S3b = 1 for static or linear hashing;

C_S3b = 1 for extendible hashing;

ⁿ        S4. Using an ordering index to retrieve multiple records:

ⁿ        For the comparison condition on a key field with an ordering index, C_S4 = x + (b/2)

ⁿ        S5. Using a clustering index to retrieve multiple records:

^ C_S5 =   x   +   ┌   (s/bfr)   ┐

ⁿ        S6. Using a secondary (B+-tree) index:

ⁿ        For an equality comparison, C_S6a = x + s;

ⁿ        For an comparison condition such as >, <, >=, or <=,

ⁿ        C_S6a = x + (b_I1/2) + (r/2)

ⁿ        S7. Conjunctive selection:

ⁿ        Use either S1 or one of the methods S2 to S6 to solve.

ⁿ        For the latter case, use one condition to retrieve the records and then check in the memory buffer whether each retrieved record satisfies the remaining conditions in the conjunction.

ⁿ        S8. Conjunctive selection using a composite index:

ⁿ        Same as S3a, S5 or S6a, depending on the type of index.

^ Examples of Cost Functions for

Join selectivity (js)

^ js = | (R   _C S) | / | R x S | = | (R   _C S) | / (|R| * |S |)

ⁿ        If condition C does not exist, js = 1;

ⁿ        If no tuples from the relations satisfy condition C, js = 0;

ⁿ        Usually, 0 <= js <= 1;

n     Size of the result file after join ^ | (R   _C S) | = js * |R| * |S |

ⁿ        J1. Nested-loop join:

ⁿ        C_J1 = b_R + (b_R*b_S) + ((js* |R|* |S|)/bfr_RS)

ⁿ        (Use R for outer loop)

ⁿ        J2. Single-loop join (using an access structure to retrieve the matching record(s))

ⁿ        If an index exists for the join attribute B of S with index levels x_B, we can retrieve each record s in R and then use the index to retrieve all the matching records t from S that satisfy t[B] = s[A].

ⁿ        The cost depends on the type of index.

ⁿ        J2. Single-loop join (contd.)

ⁿ        For a secondary index,

ⁿ        C_J2a = b_R + (|R| * (x_B + s_B)) + ((js* |R|* |S|)/bfr_RS);

ⁿ        For a clustering index,

ⁿ        C_J2b =  b_R + (|R| * (x_B + (s_B/bfr_B))) + ((js* |R|* |S|)/bfr_RS);

ⁿ        For a primary index,

ⁿ        C_J2c =  b_R + (|R| * (x_B + 1)) + ((js* |R|* |S|)/bfr_RS);

ⁿ        If a hash key exists for one of the two join attributes — B of S

ⁿ        C_J2d =  b_R + (|R| * h) + ((js* |R|* |S|)/bfr_RS);

ⁿ        J3. Sort-merge join:

ⁿ        C_J3a = C_S + b_R + b_S + ((js* |R|* |S|)/bfr_RS);

ⁿ        (CS: Cost for sorting files)

ⁿ        Multiple Relation Queries and Join Ordering

ⁿ        A query joining n relations will have n-1 join operations, and hence can have a large number of different join orders when we apply the algebraic transformation rules.

ⁿ        Current query optimizers typically limit the structure of a (join) query tree to that of left-deep (or right-deep) trees.

ⁿ        Left-deep tree:

ⁿ        A binary tree where the right child of each non-leaf node is always a base relation.

ⁿ        Amenable to pipelining

Could utilize any access paths on the base relation (the right child) when executing the join.

ⁿ        Oracle DBMS V8

ⁿ        Rule-based query optimization: the optimizer chooses execution plans based on heuristically ranked operations.

ⁿ        (Currently it is being phased out)

ⁿ        Cost-based query optimization: the optimizer examines alternative access paths and operator algorithms and chooses the execution plan with lowest estimate cost.

ⁿ        The query cost is calculated based on the estimated usage of resources such as I/O, CPU and memory needed.

ⁿ        Application developers could specify hints to the ORACLE query optimizer.

ⁿ        The idea is that an application developer might know more information about the data.

ⁿ        Semantic Query Optimization:

ⁿ        Uses constraints specified on the database schema in order to modify one query into another query that is more efficient to execute.

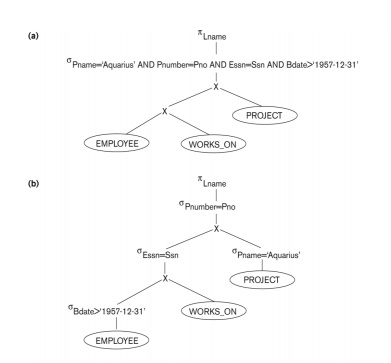
ⁿ        Consider the following SQL query,

SELECT     E.LNAME, M.LNAME

FROM EMPLOYEE E M

WHERE     E.SUPERSSN=M.SSN AND E.SALARY>M.SALARY

^ Explanation:

^ Suppose that we had a constraint on the database schema that stated that no employee

can earn more than his or her direct supervisor. If the semantic query optimizer checks

for the existence of this constraint, it need not execute the query at all because it knows that the result of the query will be empty. Techniques known as theorem proving can be used for this purpose.