Pseudorandom Number Generators

PSEUDORANDOM  NUMBER GENERATORS

In this section, we look at two types of algorithms for PRNGs.

Linear Congruential Generators

A widely used technique for pseudorandom number generation is an algorithm first proposed by Lehmer [LEHM51], which is known as the linear congruential method. The algorithm is parameterized with four numbers, as follows:

The sequence of random numbers {Xn} is obtained via the following iterative equation:

Xn + 1  = (aXn  + c)mod m

If m, a, c, and X0 are integers, then this technique will produce a sequence of integers with each integer in the range 0 … Xn 6 m.

The selection of values for a, c, and m is critical in developing a good random number generator. For  example, consider  a  =  c  =  1. The  sequence produced  is obviously  not  satisfactory. Now  consider  the values a  = 7, c  = 0, m  = 32, and X0  = 1.  This  generates  the sequence 57, 17, 23, 1, 7, etc.6,  which  is also clearly unsatisfactory. Of the 32 possible values, only four are used; thus, the sequence is said to have a period of 4. If, instead, we change the value of a to  5, then the sequence is 55, 25, 29, 17, 21, 9, 13, 1, 5, etc.6,   which   increases   the period to 8.

We would like m to be very large, so that there is the potential for producing a long series of distinct random numbers. A common criterion is that m be nearly equal to the maximum representable nonnegative integer for a given computer. Thus, a value of m near to or equal to 231 is typically chosen.

[PARK88a] proposes three tests to be used in evaluating a random number generator:

T₁: The function should be a full-period generating function. That is, the function should generate all the numbers between 0 and m before repeating.

T₂: The generated sequence should appear random.

T₃: The function should implement efficiently with 32-bit arithmetic.

With appropriate values of a, c, and m, these three tests can be passed. With respect to T1, it can be shown that if m is prime and c = 0, then for certain values of a the period of the generating function is m - 1, with only the value 0 missing. For 32- bit arithmetic, a convenient prime value of m is 231 - 1. Thus, the generating function becomes

Xn + 1 = (aXn) mod (231 - 1)

Of the more than 2 billion possible choices for a, only a handful of multipliers pass all three tests. One such value is a = 75 = 16807, which was originally selected for use in the IBM 360 family of computers [LEWI69]. This generator is widely used and has been subjected to a more thorough testing than any other PRNG. It is frequently recommended for statistical and simulation work (e.g., [JAIN91]).

The strength of the linear congruential algorithm is that if the multiplier and modulus are properly chosen, the resulting sequence of numbers will be statistically indistinguishable from a sequence drawn at  random  (but  without  replacement) from the set 1, 2, Á , m - 1. But there is nothing random at all about the algorithm, apart from the choice of the initial value X0. Once that value is chosen, the remain- ing numbers in the sequence follow deterministically. This has implications for cryptanalysis.

If an opponent knows that the linear congruential algorithm is being used and if the parameters are known (e.g., a = 75, c = 0, m = 231 - 1), then once a single number is discovered, all subsequent numbers are known. Even if the oppo- nent knows only that a linear congruential algorithm is being used, knowledge of a small part of the sequence is sufficient to determine the parameters of the algo- rithm. Suppose that the opponent is able to determine values for X0, X1, X2, and X3. Then

X1 = (aX0 + c) mod m 

X2 = (aX1 + c) mod m 

X3  = (aX2  + c) mod m

These equations can be solved for a, c, and m.

Thus, although it is nice to be able to use a good PRNG, it is desirable to make the actual sequence used nonreproducible, so that knowledge of part of the sequence on the part of an opponent is insufficient to determine future elements of the sequence. This goal can be achieved in a number of ways. For example, [BRIG79] suggests using an internal system clock to modify the random number stream. One way to use the clock would be to restart the sequence after every N numbers using the current clock value (mod m) as the new seed. Another way would be simply to add the current clock value to each random number (mod m).

Blum Blum Shub Generator

A popular approach to generating secure pseudorandom numbers is known as the Blum, Blum, Shub (BBS) generator, named for its developers [BLUM86]. It has perhaps the strongest public proof of its cryptographic strength of any purpose-built algorithm. The procedure is as follows. First, choose two large prime numbers, p and q, that both have a remainder of 3 when divided by 4. That is,

p  K  q  K  3(mod 4)

This  notation,   explained   more   fully   in   Chapter   4,   simply   means   that   (p mod 4) =  (q mod 4)  =  3. For  example, the  prime  numbers  7  and  11  satisfy 7 K 11 K 3(mod 4). Let n = p * q. Next, choose a random number s, such that s is relatively prime to n; this is equivalent to saying that neither p nor q is a factor of s. Then the BBS generator produces a sequence of bits Bi according to the following algorithm:

X0     =   s2 mod n

for i =  1 to q

Xi  = (Xi - 1)2 mod n

Bi   =   Xi  mod 2

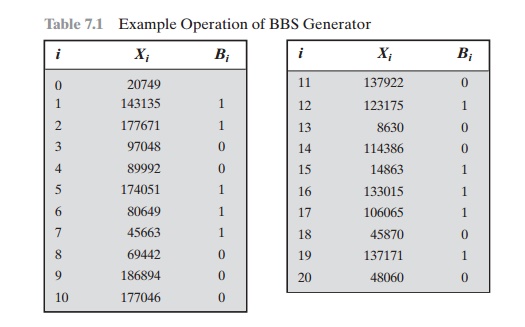
Thus, the least significant bit is taken at each iteration. Table 7.1, shows an example of BBS operation. Here, n = 192649 = 383 * 503, and the seed s = 101355.

The BBS is referred to as a cryptographically secure pseudorandom bit generator (CSPRBG). A CSPRBG is defined as one that passes the next-bit test, which, in turn, is defined as follows [MENE97]: A pseudorandom bit generator is said to pass the next-bit test if there is not a polynomial-time   algorithm2 that, on

input of the first k bits of an output sequence, can predict the (k + 1)st bit with probability significantly greater than 1/2. In other words, given the first k bits of the sequence, there is not a practical algorithm that can even allow you to state that the next bit will be 1 (or 0) with probability greater than 1/2. For all practical purposes, the sequence is unpredictable. The security of BBS is based on the difficulty of factoring n. That is, given n, we need to determine its two prime factors p and q.

Table 7.1   Example Operation of BBS Generator