Principles of Pseudorandom Number Generation

PRINCIPLES OF PSEUDORANDOM NUMBER  GENERATION

Random numbers play an important role in the use of encryption for various net- work security applications. In this section, we provide a brief overview of the use of random numbers in cryptography and network security and then focus on the prin- ciples of pseudorandom number generation.

The Use of Random Numbers

A number of network security algorithms and protocols based on cryptography make use of random binary numbers. For example,

•                           Key distribution and reciprocal authentication schemes, such as those discussed in Chapters 14 and 15. In such schemes, two communicating parties cooperate by exchanging messages to distribute keys and/or authenticate each other. In many cases, nonces are used for handshaking to prevent replay attacks. The use of random numbers for the nonces frustrates an opponent’s efforts to deter- mine or guess the nonce.

•                           Session key generation. We will see a number of protocols in this book where a secret key for symmetric encryption is generated for use for a short period of time. This key is generally called a session key.

•                           Generation of keys for the RSA public-key encryption algorithm (described in Chapter 9).

•                           Generation of a bit stream for symmetric stream encryption (described in this chapter).

These applications give rise to two distinct and not necessarily compatible requirements for a sequence of random numbers: randomness and unpredictability.

RANDOMNESS Traditionally, the concern in the generation of a sequence of allegedly random numbers has been that the sequence of numbers be random in some well- defined statistical sense. The following two criteria are used to validate that a sequence of numbers is random:

•                           Uniform distribution: The distribution of bits in the sequence should be uniform; that is, the frequency of occurrence of ones and zeros should be approximately equal.

•                           Independence: No one subsequence in the sequence can be inferred from the others.

Although there are well-defined tests for determining that a sequence of bits matches a particular distribution, such as the uniform distribution, there is no such test to “prove” independence. Rather, a number of tests can be applied to demon- strate if a sequence does not exhibit independence. The general strategy is to apply a number of such tests until the confidence that independence exists is sufficiently strong.

In the context of our discussion, the use of a sequence of numbers that appear statistically random often occurs in the design of algorithms related to cryptography. For example, a fundamental requirement of the RSA public-key encryption scheme discussed in Chapter 9 is the ability to generate prime numbers. In general, it is dif- ficult to determine if a given large number N is prime. A brute-force approach would be to divide N by every odd integer less than 1N. If N is on the order, say, of 10150, which is a not uncommon occurrence in public-key cryptography, such a brute-force approach is beyond the reach of human analysts and their computers. However, a number of effective algorithms exist that test the primality of a number by using a sequence of randomly chosen integers as input to relatively simple computations. If the sequence is sufficiently long (but far, far less than 210150), the primality of a number can be determined with near certainty. This type of approach, known as randomization, crops up frequently in the design of algorithms. In essence, if a problem is too hard or time-consuming to solve exactly, a    simpler, shorter approach based on randomization is used to provide an answer with any desired level of confidence.

UNPREDICTABILITY In applications such as reciprocal authentication, session key generation, and stream ciphers, the requirement is not just that the sequence of numbers be statistically random but that the successive members of the sequence are unpredictable. With “true” random sequences, each number is statistically independent of other numbers in the sequence and therefore unpredictable. However, as is discussed shortly, true random numbers are seldom used; rather, sequences of numbers that appear to be random are generated by some algorithm. In this latter case, care must be taken that an opponent not be able to predict future elements of the sequence on the basis of earlier elements.

TRNGs, PRNGs, and PRFs

Cryptographic applications typically make use of algorithmic techniques for ran- dom number generation. These algorithms are deterministic and therefore produce sequences of numbers that are not statistically random. However, if the algorithm is good, the resulting sequences will pass many reasonable tests of randomness. Such numbers are referred to as pseudorandom numbers.

You may be somewhat uneasy about the concept of using numbers generated by a deterministic algorithm as if they were random numbers. Despite what might be called philosophical objections to such a practice, it generally works. As one expert on probability theory puts it [HAMM91]:

For practical purposes we are forced to accept the awkward concept of “relatively random” meaning that with regard to the proposed use we can see no reason why they will not perform as if they were random (as the theory usually requires). This is highly subjective and is not very palatable to purists, but it is what statisticians regu- larly appeal to when they take “a random sample” —they hope that any results they use will have approximately the same properties as a complete counting of the whole sample space that occurs in their theory.

Figure 7.1 contrasts a true random number generator (TRNG) with two forms of pseudorandom number generators. A TRNG takes as input a source that is effec- tively random; the source is often referred to as an entropy source. We discuss such sources in Section 7.6. In essence, the entropy source is drawn from the physical environment of the computer and could include things such as keystroke timing patterns, disk electrical activity, mouse movements, and instantaneous values of the system clock. The source, or combination of sources, serve as input to an algorithm that produces random binary output. The TRNG may simply involve conversion of an analog source to a binary output. The TRNG may involve additional processing to overcome any bias in the source; this is discussed in Section 7.6.

In contrast, a PRNG takes as input a fixed value, called the seed, and produces a sequence of output bits using a deterministic algorithm. Typically, as shown, there is some feedback path by which some of the results of the algorithm are fed back as  

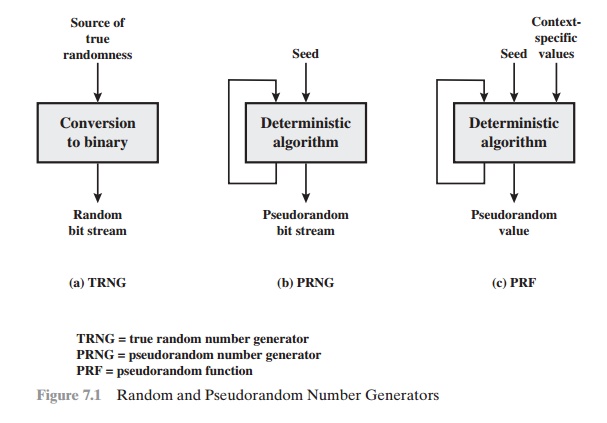
input as additional output bits are produced. The important thing to note is that the output bit stream is determined solely by the input value or values, so that an adver- sary who knows the algorithm and the seed can reproduce the entire bit stream.

Figure 7.1 shows two different forms of PRNGs, based on application.

•                           Pseudorandom number generator: An algorithm that is used to produce an open-ended sequence of bits is referred to as a PRNG. A common application for an open-ended sequence of bits is as input to a symmetric stream cipher, as discussed in Section 7.4. Also, see Figure 3.1a.

•                           Pseudorandom function (PRF): A PRF is used to produced a pseudorandom string of bits of some fixed length. Examples are symmetric encryption keys and nonces. Typically, the PRF takes as input a seed plus some context specific values, such as a user ID or an application ID. A number of examples of PRFs will be seen throughout this book, notably in Chapters 16 and 17.

Other than the number of bits produced, there is no difference between a PRNG and a PRF. The same algorithms can be used in both applications. Both require a seed and both must exhibit randomness and unpredictability. Further, a PRNG application may also employ context-specific input. In what follows, we make no distinction between these two applications.

PRNG Requirements

When a PRNG or PRF is used for a cryptographic application, then the basic requirement is that an adversary who does not know the seed is unable to deter- mine the pseudorandom string. For example, if the pseudorandom bit stream   is used in a stream cipher, then knowledge of the pseudorandom bit stream would enable the adversary to recover the plaintext  from  the  ciphertext. Similarly, we wish to protect the output value of a PRF. In this latter case, consider the following scenario. A 128-bit seed, together with some context-specific values, are used to generate a 128-bit secret key that is subsequently used for symmetric encryption. Under normal circumstances, a 128-bit key is safe from a brute-force attack. However, if the PRF does not generate effectively random 128-bit output values, it may be possible for an adversary to narrow the possibilities and successfully use a brute  force attack.

This general requirement for secrecy of the output of a PRNG or PRF leads to specific requirements in the areas of randomness, unpredictability, and the character- istics of the seed. We now look at these in turn.

RANDOMNESS In terms of randomness, the requirement for a PRNG is that the generated bit stream appear random even though it is deterministic. There is no single test that can determine if a PRNG generates numbers that have the characteristic of randomness. The best that can be done is to apply a sequence of tests to the PRNG. If the PRNG exhibits randomness on the basis of multiple tests, then it can be assumed to satisfy the randomness requirement. NIST SP 800-22 (A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications) specifies that the tests should seek to establish the following three characteristics.

•                 Uniformity: At any point in the generation of a sequence of random or pseudorandom bits, the occurrence of a zero or one is equally likely, i.e., the probability of each is exactly 1/2. The expected number of zeros (or ones) is n/2, where n = the sequence length.

•                 Scalability: Any test applicable to a sequence can also be applied to subse- quences extracted at random. If a sequence is random, then any such extracted subsequence should also be random. Hence, any extracted subsequence should pass any test for randomness.

•                 Consistency: The behavior of a generator must be consistent across starting values (seeds). It is inadequate to test a PRNG based on the output from a sin- gle seed or an TRNG on the basis of an output produced from a single physi- cal output

SP 800-22 lists 15 separate tests of randomness. An understanding of these tests requires a basic knowledge of statistical analysis, so we don’t attempt a techni- cal description here. Instead, to give some flavor for the tests, we list three of the tests and the purpose of each test, as follows.

•                 Frequency test: This is the most basic test and must be included in any test suite. The purpose of this test is to determine whether the number of ones and zeros in a sequence is approximately the same as would be expected for a truly random sequence.

Runs test: The focus of this test is the total number of runs in the sequence, where a run is an uninterrupted sequence of identical bits bounded before and after with a bit of the opposite value. The purpose of the runs test is to determine whether the number of runs of ones and zeros of various lengths is as expected for a random sequence.

•                           Maurer’s universal statistical test: The focus of this test is the number of bits between matching patterns (a measure that is related to the length of a com- pressed sequence). The purpose of the test is to detect whether or not the sequence can be significantly compressed without loss of information. A signifi- cantly compressible sequence is considered to be non-random.

UNPREDICTABILITY A stream of pseudorandom numbers should exhibit two forms of unpredictability:

•                           Forward unpredictability: If the seed is unknown, the next output bit in the sequence should be unpredictable in spite of any knowledge of previous bits in the sequence.

•                           Backward unpredictability: It should also not be feasible to determine the seed from knowledge of any generated values. No correlation between a seed and any value generated from that seed should be evident; each element of the sequence should appear to be the outcome of an independent random event whose probability is 1/2.

The same set of tests for randomness also provide a test of unpredictability. If the generated bit stream appears random, then it is not possible to predict some bit or bit sequence from knowledge of any previous bits. Similarly, if the bit sequence appears random, then there is no feasible way to deduce the seed based on the bit sequence. That is, a random sequence will have no correlation with a fixed value (the seed).

SEED REQUIREMENTS For cryptographic applications, the seed that serves as input to the PRNG must be secure. Because the PRNG is a deterministic algorithm, if the adversary can deduce the seed, then the output can also be determined. Therefore, the seed must be unpredictable. In fact, the seed itself must be a random or pseudorandom number.

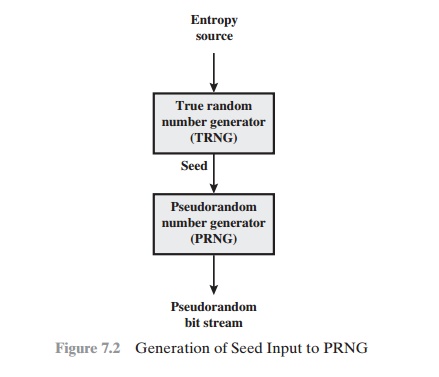
Typically, the seed is generated by a TRNG, as shown in Figure 7.2. This is the scheme recommended by SP800-90. The reader may wonder, if a TRNG is available, why it is necessary to use a PRNG. If the application is a stream cipher, then a TRNG is not practical. The sender would need to generate a keystream of bits as long as the plaintext and then transmit the keystream and the ciphertext securely to the receiver. If a PRNG is used, the sender need only find a way to deliver the stream cipher key, which is typically 54 or 128 bits, to the receiver in a secure fashion.

Even in the case of a PRF application, in which only a limited number of bits is generated, it is generally desirable to use a TRNG to provide the seed to the PRF and use the PRF output rather then use the TRNG directly. As is explained in a Section 7.6, a TRNG may produce a binary string with some bias. The PRF would have the effect of “randomizing” the output of the TRNG so as to eliminate that bias.

Finally, the mechanism used to generate true random numbers may not be able to generate bits at a rate sufficient to keep up with the application requiring the random bits.

Algorithm Design

Cryptographic PRNGs have been the subject of much research over the years, and a wide variety of algorithms have been developed. These fall roughly into two categories.

•                 Purpose-built algorithms: These are algorithms designed specifically and solely for the purpose of generating pseudorandom bit streams. Some of these algo- rithms are used for a variety of PRNG applications; several of these are described in the next section. Others are designed specifically for use in a stream cipher. The most important example of the latter is RC4, described in Section 7.5.

•                 Algorithms based on existing cryptographic algorithms: Cryptographic algo- rithms have the effect of randomizing input. Indeed, this is a requirement of such algorithms. For example, if a symmetric block cipher produced ciphertext that had certain regular patterns in it, it would aid in the process of cryptanalysis. Thus, cryptographic algorithms can serve as the core of PRNGs. Three broad categories of cryptographic algorithms are commonly used to create PRNGs:

—Symmetric block ciphers: This approach is discussed in Section    7.3.

—Asymmetric ciphers: The number theoretic concepts used for an asymmetric cipher can also be adapted for a PRNG; this approach is examined in Chapter 10.

—Hash functions and message authentication codes: This approach is examined in Chapter 12.

Any of these approaches can yield a cryptographically strong PRNG. A purpose-built algorithm may be provided by an operating system for general use. For applications that already use certain cryptographic algorithms for encryption or authentication, it makes sense to reuse the same code for the PRNG. Thus, all of these approaches are in common use.