Chapter: Cryptography and Network Security Principles and Practice : One Symmetric Ciphers : Pseudorandom Number Generation and Stream Ciphers
Pseudorandom Number Generation Using a Block Cipher
PSEUDORANDOM NUMBER
GENERATION USING A BLOCK CIPHER
A popular approach
to PRNG construction is to use a symmetric block cipher as the
heart of the PRNG mechanism. For any block of plaintext, a symmetric block cipher
produces an output block that is apparently random. That is, there
are no patterns or
regularities in the ciphertext that provide information that can be used to
deduce the plaintext. Thus, a symmetric block cipher is a good candidate for building a pseudorandom number generator.
If an established, standardized block cipher is used, such as DES or AES, then
the security characteristics of the PRNG can be established. Further, many applica- tions already make use of DES or AES, so the inclusion
of the block cipher as part
of the PRNG algorithm is straightforward.
PRNG Using Block Cipher Modes of Operation
Two approaches that use a block cipher to build a PNRG have gained widespread
acceptance: the CTR mode and the OFB mode. The CTR mode is recommended in SP 800-90, in the ANSI standard X9.82
(Random Number Generation), and in RFC 4086. The OFB mode is recommended in X9.82 and RFC 4086.
Figure 7.3 illustrates the two methods. In each case, the
seed consists of two parts: the encryption key value and a value V that will be updated after each block of pseudorandom numbers is
generated. Thus, for AES-128, the
seed consists of a 128-bit key and a 128-bit V value. In the CTR case, the value of V is incremented by 1 after each encryption. In the case of OFB, the value of V is updated to equal the value of the
preceding PRNG block. In both cases, pseudorandom bits are produced
one block at a time (e.g., for AES, PRNG
bits are generated 128 bits at a time).

The CTR algorithm for PRNG can be summarized as follows.
while (len (temp) < requested_number_of_bits) do
V = (V + 1) mod 2128.
output_block = E(Key, V) temp = temp ||
ouput_block
The OFB algorithm can be summarized as follows.
while (len (temp) < requested_number_of_bits) do
V = E(Key, V)
temp = temp || V
To get some idea of the performance of these two PRNGs, consider the fol- lowing short experiment. A random bit sequence
of 256 bits was obtained from
random.org, which uses three radios tuned between
stations to pick up atmospheric noise. These 256 bits form the seed, allocated as
Key: cfb0ef3108d49cc4562d5810b0a9af60
V: 4c89af496176b728ed1e2ea8ba27f5a4
The total number of one bits in the 256-bit seed is 124,
or a fraction of 0.48, which is reassuringly close to the ideal of 0.5.
For the OFB PRNG, Table 7.2 shows the first eight output
blocks (1024 bits) with two rough measures
of security. The second column shows the fraction of one
bits in each 128-bit block.
This corresponds to one of the NIST
tests. The results indi- cate that the output is split
roughly equally between zero and one bits. The third column shows the fraction
of bits that match between
adjacent blocks. If this num- ber
differs substantially from 0.5, that
suggests a correlation between blocks, which could be a security
weakness. The results suggest
no correlation.
Table 7.2 Example Results for PRNG Using OFB

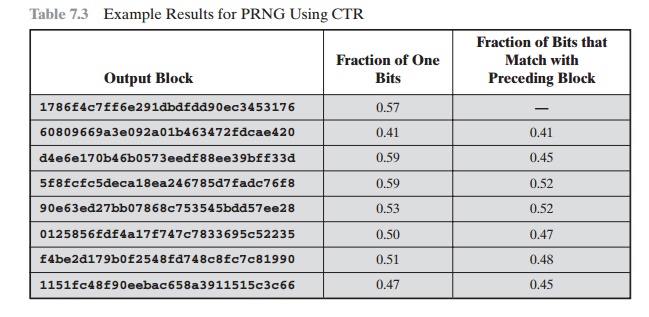
Table 7.3 shows the results using the same key and V values for CTR mode.
Again, the results are favorable.
ANSI X9.17 PRNG
One of the strongest
(cryptographically speaking) PRNGs is specified
in ANSI X9.17. A number of applications employ
this technique, including financial security
applications and PGP (the latter described in Chapter 18).
Figure 7.4 illustrates the algorithm, which makes use of
triple DES for encryption. The ingredients are as follows.
•
Input: Two pseudorandom inputs
drive the generator. One is a 64-bit repre- sentation
of the current date and time, which is updated
on each number generation. The other is a 64-bit seed value; this is initialized to some arbitrary value and is updated
during the generation process.
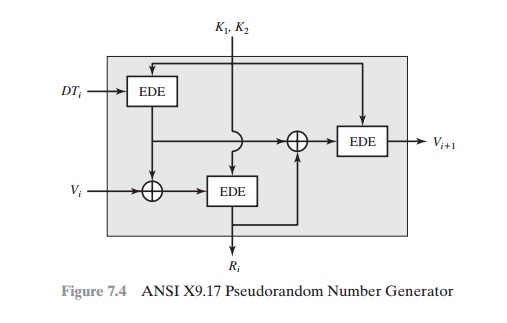
•
Keys: The generator makes use of three triple DES encryption modules. All three make use of the same pair of 56-bit keys, which
must be kept secret and are used only for pseudorandom number generation.
•
Output: The
output consists of a 64-bit pseudorandom number and a 64-bit seed value.
Let us define the following
quantities.

where EDE([K1, K2],X) refers to
the sequence encrypt-decrypt-encrypt using two- key triple DES to encrypt X.
Several factors contribute
to the cryptographic strength of this method. The
technique involves a 112-bit key and three
EDE encryptions for a total
of nine DES encryptions. The scheme is driven by two pseudorandom inputs, the date and time value, and a seed produced by the generator that is distinct
from the pseudorandom number produced
by the generator. Thus, the amount
of material that must be com-
promised by an opponent is overwhelming. Even if a pseudorandom number Ri were compromised, it would be impossible to deduce the Vi + 1 from the Ri, because an additional EDE operation is used to produce the Vi + 1.
Related Topics