Prime and Composite Numbers

Prime and Composite Numbers

Think about the situation:

The teacher gave 5 buttons to Anbuselvan and 6 buttons to Kayalvizhi and asked them to arrange the buttons in all possible rows such that the number of buttons in each row is equal. They did it, in different ways as shown below:

Anbuselvan’s Ways

He realises that 5 buttons can be arranged in only 2 rectangular ways. Hence, the only factors of 5 are 1 and 5 (number of rows).

Kayalvizhi’s Ways

She realises that 6 buttons can be arranged in 4 rectangular ways. Hence, the factors of 6 are 1, 2, 3 and 6 (number of rows).

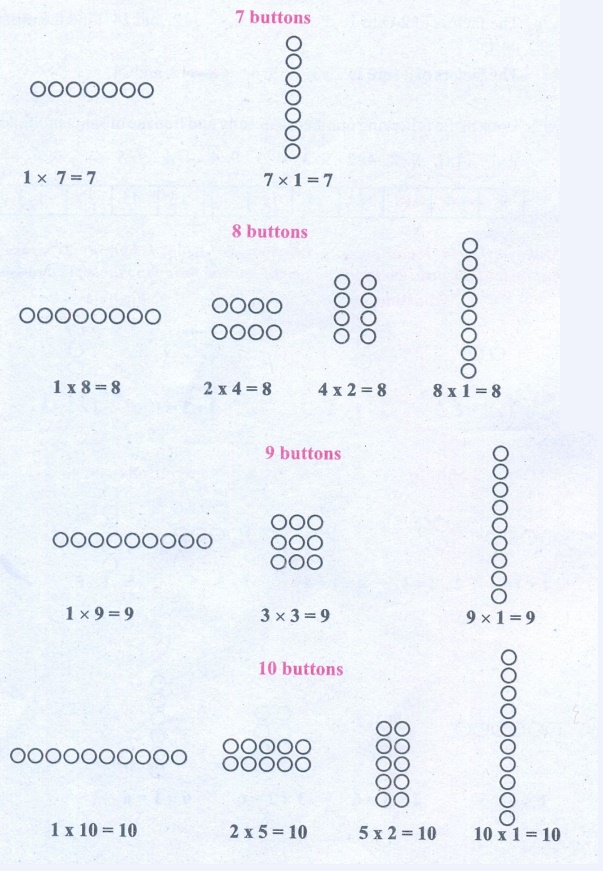
* Make different rectangular arrangements using 1 button, 2 buttons, 3 buttons, 4 buttons,…, 10 buttons and complete the following table:

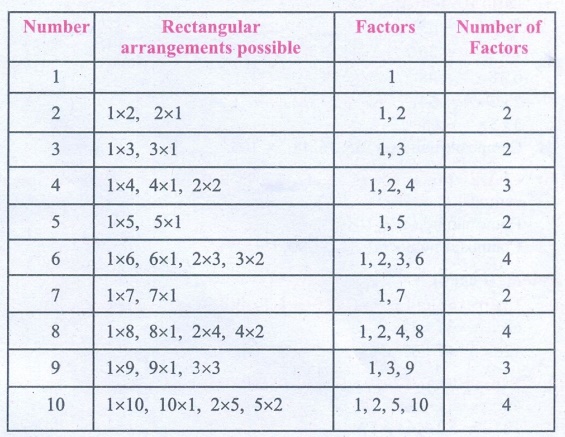
From the table, we conclude that

* A natural number greater than 1, having only two factors namely 1 and the number itself, is called a prime number.

For example, 2 (1 × 2) is a prime number as is 13 (1 × 13).

* A natural number having more than 2 factors is called a composite number.

For example, 15 is a composite number (15 = 1 × 3 × 5) as is 70 (1 × 2 × 5 × 7).

A number is a perfect number if the sum of its factors other than the given number gives the same number. For example, 6 is a perfect number, since adding the factors of 6 (other than 6), namely 1, 2 and 3 gives the given number 6. i.e.,1+2+3 = 6 is the given number.

Check whether 28, 54 and 496 are perfect numbers or not.

Activity

(i) List out the prime and composite numbers represented by the dates in the month of October.

By the dates in the month of October

Prime numbers : 2,3,5,7,11,13,17,19,23,29,31

Composite numbers : 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30.

(ii) Generate a few composite numbers by product of two or more natural numbers.

7 × 5 = 35

9 × 4 = 36

6 × 8 = 48

2 × 3 × 9 = 54

3 × 5 × 7 = 105

Composite numbers: 35,36,48,54,105.

(iii) Classify the numbers 34, 57, 71, 93, 101, 111 and 291 as prime or composite.

Prime numbers: 71,101

Composite numbers: 34, 57, 93, 111, 291

1. Finding the Prime Numbers by Sieve of Eratosthenes Method

Sieve of Eratosthenes, is a simple method of elimination by which we can easily find the prime numbers upto a given number. This method given by a Greek Mathematician, Eratosthenes of Alexandria, follows some simple steps which are listed below, by which we can find the prime numbers.

Step 1: Create 10 rows and 10 columns and write the numbers from 1 to 10 in the first row, 11 to 20 in the second row and continue the same as 91 to 100 in the tenth row.

Step 2: Leave 1 as it is neither prime nor composite (Why?). Start with the smallest prime 2.

Encircle and colour 2 and cross out all other multiples of 2 (all even numbers) in the grid.

Step 3: Now, take the next prime 3. Encircle and colour 3 and cross out all other multiples of 3 in the grid.

Step 4: As 4 is crossed out already, go for the next prime 5 and cross out multiples of 5, except 5.

Step 5: Keep doing this, for two more primes 7 and 11 and stop. (Think why?)

The above steps are carried out to find prime numbers upto 100 in the following grid.

SIEVE OF ERATOSTHENES

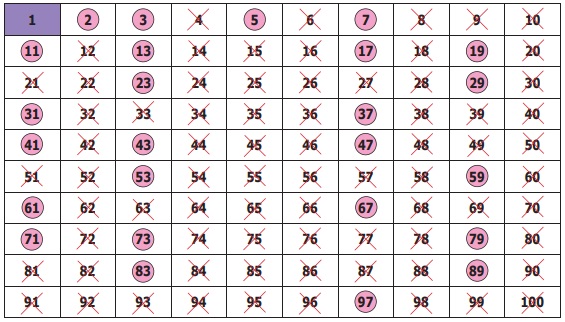
From the Sieve of Eratosthenes, we observe that,

* The crossed-out numbers are composite and the coloured numbers (encircled) are primes. The total number of primes upto 100 is 25.

* The only prime number that ends with 5 is 5.

2. Expressing a Number as the Sum of Prime Numbers

Any number can always be expressed as the sum of two or more prime numbers. Let us illustrate this in the following examples.

Example 1: Express 42 and 100 as the sum of two consecutive primes.

Solution: 42 = 19+23;

                100 = 47+53

Example 2: Express 31 and 55 as the sum of any three odd primes.

Solution: 31 = 5+7+19 (find another way, if possible )

                 55 = 3 + 23+29

Try these

(i) Express 68 and 128 as the sum of two consecutive primes.

68 = 31 + 37

128 = 61 + 37

(ii) Express 79 and 104 as the sum of any three odd primes.

79 = 11 + 31 + 37

104 = 2 + 43 + 59

3. Twin Primes

A pair of prime numbers whose difference is 2, is called twin primes.

For example, (5, 7) is a twin prime pair as is (17,19).

Try to find a few more twin prime pairs!

If three successive prime numbers differ by 2, then the prime numbers form a prime triplet. The only prime triplet is (3, 5, 7).